назад | ОГЛАВЛЕНИЕ | вперед
2.5. Переходные процессы в механической части электропривода
Рассмотрим
переходные процессы в механической части электропривода, представленной жестким
механическим звеном.
Допустим, что
начальная скорость равна нулю: 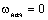 , а к ротору двигателя в момент времени t=0
прикладывается электромагнитный момент двигателя, изменяющийся по
экспоненциальному закону с постоянной времени Т. , а к ротору двигателя в момент времени t=0
прикладывается электромагнитный момент двигателя, изменяющийся по
экспоненциальному закону с постоянной времени Т.
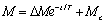 (2.28) (2.28)
Решим
уравнение электропривода 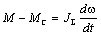 относительно
дифференциала скорости: относительно
дифференциала скорости: 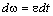 , где , где 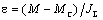 - ускорение масс механической части. - ускорение масс механической части.
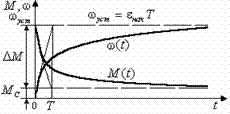
Рис.2.16. Переходный процесс пуска электропривода при экспоненциальной зависимости M(t).
Проинтегрируем
обе части полученного равенства при заданном законе изменения движущего
момента:
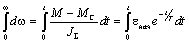
В результате
получим (рис. 2.16):
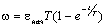
где
 - начальное ускорение;
- начальное ускорение;
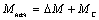 -начальный момент двигателя. -начальный момент двигателя.
Время
переходного процесса практически можно считать равным t n . n. =(3÷4)T (рис. 2.16).
Рассмотрим
условия движения электропривода при постоянных моментах двигателя и
сопротивления, т.е. 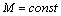 и и  (рис. 2.17а). В результате интегрирования уравнения (рис. 2.17а). В результате интегрирования уравнения 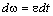
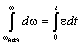 , ,
т. е. получим известную формулу
равномерно ускоренного движения:
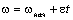 . .
С помощью
этого выражения можно определить время переходного процесса t n.n. изменения скорости
от начального значения 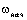 до конечного значения до конечного значения 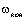 : :
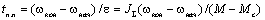 (2.29) (2.29)
При 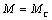 , , 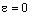 электропривод
сохраняет состояние покоя ( электропривод
сохраняет состояние покоя ( 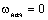 ) или равномерного движения ( ) или равномерного движения ( 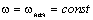 ) до тех пор, пока равенство ) до тех пор, пока равенство 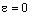 не будет нарушено. В
момент t=0 момент двигателя скачком увеличивается до значения не будет нарушено. В
момент t=0 момент двигателя скачком увеличивается до значения 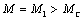 и электропривод сразу
переходит в режим равномерно ускоренного движения с ускорением и электропривод сразу
переходит в режим равномерно ускоренного движения с ускорением 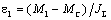 . Если оставить момент двигателя неизменным, т. е. . Если оставить момент двигателя неизменным, т. е. 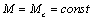 , этот режим будет длиться сколь угодно долго, а скорость
неограниченно возрастать. На практике при достижении электроприводом требуемой
скорости момент двигателя снижается до значения , этот режим будет длиться сколь угодно долго, а скорость
неограниченно возрастать. На практике при достижении электроприводом требуемой
скорости момент двигателя снижается до значения 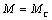 (в момент времени (в момент времени 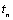 ), ускорение скачком уменьшается до нуля и наступает
статический установившийся режим при значениях ), ускорение скачком уменьшается до нуля и наступает
статический установившийся режим при значениях 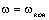 (рис. 2.17а). (рис. 2.17а).
Допустим, что
система нагружена активным моментом МС,
обусловленным, например, весом поднимаемого груза, и работает в установившемся
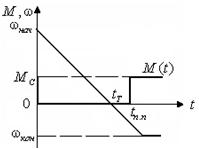
режиме подъёма груза с постоянной скоростью при М= МС (рис. 2.17б). Если в момент времени t=0 уменьшить момент двигателя до нуля, то под действием
момента МС привод станет
замедляться, при этом 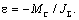 Скорость в
соответствии с уравнением Скорость в
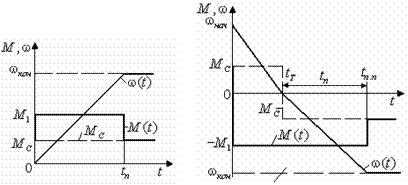
соответствии с уравнением 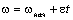 изменяется по закону: изменяется по закону:
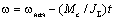 (2.30) (2.30)
а) в)
б)
Рис.
2.17. Переходные процессы электропривода в режиме равномерно ускоренного
движения (а); равномерно замедленного движения (б); реверса скорости (в).
Через время
торможения 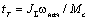 , скорость двигателя становится равной нулю, но активный
момент сохраняет своё значение и в соответствии с законом изменения скорости
двигатель начнёт ускоряться в противоположном направлении, двигаясь под
действием падающего груза с возрастающей по абсолютному значению скоростью. Так
как скорость может увеличиться до опасных значений, то двигатели снабжаются
механическим тормозом, который автоматически затормаживает привод после
отключения от сети. , скорость двигателя становится равной нулю, но активный
момент сохраняет своё значение и в соответствии с законом изменения скорости
двигатель начнёт ускоряться в противоположном направлении, двигаясь под
действием падающего груза с возрастающей по абсолютному значению скоростью. Так
как скорость может увеличиться до опасных значений, то двигатели снабжаются
механическим тормозом, который автоматически затормаживает привод после
отключения от сети.
В момент
времени 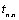 , когда достигается требуемое значение скорости , когда достигается требуемое значение скорости 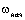 , момент двигателя скачком увеличивается от 0 до М= МС и наступает статический
режим работы с , момент двигателя скачком увеличивается от 0 до М= МС и наступает статический
режим работы с 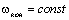 (рис. 2.17б). (рис. 2.17б).
Рассмотрим
процесс реверса электропривода при реактивном моменте МС от начальной скорости 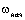 одного направления до конечной скорости одного направления до конечной скорости 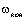 противоположного знака (рис. 2.17в). В момент времени t=0 момент двигателя скачком изменяется от значения противоположного знака (рис. 2.17в). В момент времени t=0 момент двигателя скачком изменяется от значения 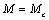 до значения до значения 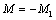 и происходит замедление системы по закону: и происходит замедление системы по закону:
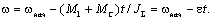 (2.31) (2.31)
Время торможения
определяется выражением:
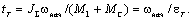 (2.32) (2.32)
При значениях 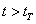 скорость двигателя под действием момента скорость двигателя под действием момента 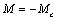 меняет свой знак, что
вызывает изменение направления реактивной нагрузки МС на противоположное (-МС). Скачком уменьшается
значение ускорения от значения, определяемого выражением меняет свой знак, что
вызывает изменение направления реактивной нагрузки МС на противоположное (-МС). Скачком уменьшается
значение ускорения от значения, определяемого выражением 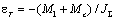 до значения, определяемого выражением до значения, определяемого выражением 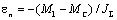 . При пуске в обратном направлении скорость изменяется
следующим образом: . При пуске в обратном направлении скорость изменяется
следующим образом:
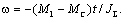
Время пуска до
скорости 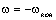 : :
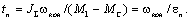 (2.33) (2.33)
Для перехода к
статическому режиму при скорости 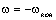 момент двигателя должен скачком уменьшиться до значения момент двигателя должен скачком уменьшиться до значения 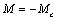 (рис. 2.17 в). (рис. 2.17 в).
Таким образом,
при постоянстве статического момента сопротивления закон изменения скорости
привода в переходных процессах определяется характером изменения во времени
момента двигателя. Для экспоненциального закона необходимо обеспечить
экспоненциальную зависимость момента от времени; для получения равномерно
ускоренного процесса пуска необходимо формировать прямоугольный закон изменения
момента от времени и т.п.
Механическая
часть, представленная в виде жёсткого приведённого звена, отражает движение
системы в среднем и не даёт точных представлений о характере движения упруго
связанных масс электропривода. Поэтому рассмотрим на простейшем примере влияние
упругих связей.
Проанализируем
переходный процесс пуска электропривода с механической частью в виде двухмассовой упругой системы (рис. 2.18) при 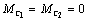 и приложении к системе
скачком электромагнитного момента двигателя и приложении к системе
скачком электромагнитного момента двигателя 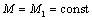 : :
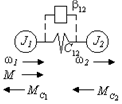
Рис. 2.18. Двухмассовая упругая система
Дифференциальное
уравнение движения системы, решенное относительно скорости двигателя 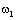 , можно получить с помощью рассмотренной выше передаточной
функции (2.26): , можно получить с помощью рассмотренной выше передаточной
функции (2.26):
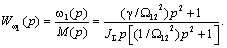
Отсюда:
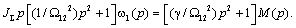
Заменив
оператор p на производную 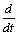 и приняв M(p)=M1, получим: и приняв M(p)=M1, получим:
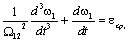
где

- среднее ускорение системы.
Корни
характеристического уравнения были определены выше:
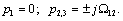
Нулевой корень
определяет частное решение, соответствующее равномерно ускоренному движению: 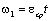 (проверяется подстановкой в дифференциальное уравнение).
Чисто мнимые корни определяют возможность развития незатухающих колебаний с
частотой (проверяется подстановкой в дифференциальное уравнение).
Чисто мнимые корни определяют возможность развития незатухающих колебаний с
частотой 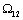 , поэтому общее решение следует искать в виде: , поэтому общее решение следует искать в виде:
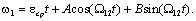
Для нахождения
коэффициентов 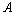 и и 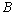 необходимо использовать начальные условия: при t=0, необходимо использовать начальные условия: при t=0, 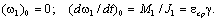
Подставив эти значения в
общее решение, получим:
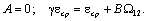
Следовательно,
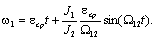 (2.34) (2.34)
В соответствии с
уравнениями движения двухмассовой системы:
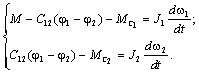
Уравнение
движения первой массы:
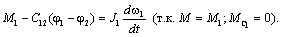
Продифференцировав
его по времени, запишем относительно скорости 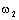 (М1=const): (М1=const):
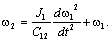 (2.35) (2.35)
Подставив
полученные выше выражения для 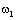 , получим: , получим:
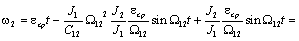
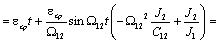
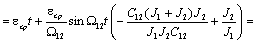
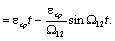 (2.36) (2.36)
Характер
полученных зависимостей ω1(t) и ω2(t) при γ<2 показан на
рисунках 2.19а и 2.19б. При М=const переходные процессы
протекают равномерно ускоренно, однако, мгновенные скорости ω1
и ω2 не совпадают, т.к. содержат
колебательные составляющие, причём колебания ω1
и ω 2 совершаются в противофазе. Из
выражения для ω2 следует, что производная
скорости второй массы dω2/dt всегда положительна,
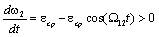
а для
принятого значения γ<2 и dω1/dt>0.
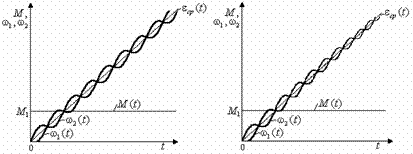
а) б)
Рис. 2.19. Пуск электропривода с двухмассовой
упругой механической частью при моменте двигателя 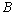 без учета (а) и с
учетом (б) естественного демпфирования. без учета (а) и с
учетом (б) естественного демпфирования.
При прочих
равных условиях колебания скорости ω1
тем меньше, чем меньше J2, а увеличение Ω12 при тех же ускорениях εср
снижает амплитуды колебаний скорости обеих масс.
В реальной системе
всегда имеются диссипативные силы типа вязкого внутреннего трения, поэтому
колебательная составляющая скоростей с течением времени затухает. Однако
естественное затухание не велико ( 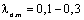 ) и за время затухания совершается 10-30 колебаний
(рис.2.19б, ) и за время затухания совершается 10-30 колебаний
(рис.2.19б, 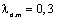 ). Даже при наибольших значениях ). Даже при наибольших значениях 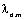 естественное демпфирование незначительно сказывается на
характере переходных процессов. естественное демпфирование незначительно сказывается на
характере переходных процессов.
назад | ОГЛАВЛЕНИЕ | вперед
| 
