Содержание  Главная (библиотека)
Предыдущий § Следущий

2-4. Работа при нагрузке

а) Первичный ток. Работа трансформатора при нагрузке характеризуется наличием тока I₂ во вторичной обмотке, увеличение которого (как будет ясно из последующего) вызывает увеличение тока I₁ в первичной обмотке.

При нагрузке трансформатора магнитный поток Ф в его сердечнике, называемый главным потоком, создается согласно закону полного тока совместным действием н. с. обеих обмоток:

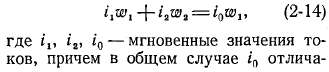ется от мгновенного значения тока холостого хода.

Так как мы принимаем токи синусоидальными, то можем написать (рис. 2-1):

б) Уравнения напряжений. Будем вначале считать, что потокосцеп-ления обмоток трансформатора пропорциональны их токам и что магнитные потери в сердечнике отсутствуют (такие условия получаются в воздушном трансформаторе). При этом, так же как для двух магнитно связанных контуров, можем написать следующие уравнения напряжений первичной и вторичной обмоток трансформатора:

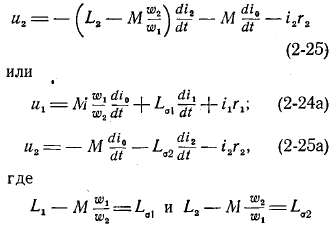
— индуктивности рассеяния первичной и вторичной обмоток; им соответствуют э. д. с. рассеяния:

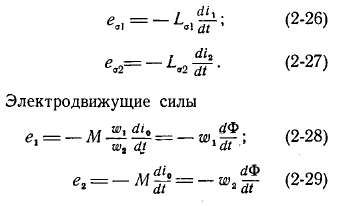рассматриваются как э. д. с, наведенные главным потоком Ф.

Приведем здесь уравнения, относящиеся к общей теории двух магнитно связанных обмоток. Для потокосцеплений этих обмоток можем написать:

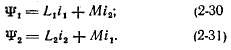Вычтем и прибавим с правой стороны написанных равенств одни и те же величины:

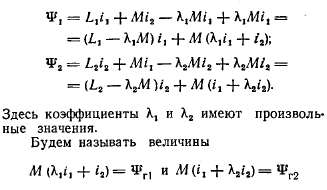главными потокосцеплениями обмоток, а величины

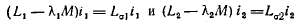их потокосцеплениями рассеяния. Главными индуктивностями обмоток назовем величины

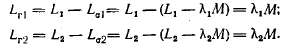
Общий коэффициент рассеяния равен:

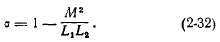Коэффициенты рассеяния обмоток равны отношениям индуктивностей рассеяния к главным индуктивностям:

Подразделяя произведение λ₁λ₂=1 любым образом на λ₁ и λ₂, можно потокосцепления рассеяния приписать одной или другой обмотке или обеим обмоткам. Мы не имеем также достаточно данных, чтобы однозначно определить главный поток, о котором говорилось ранее. Однако внести определенность в понятия индуктивностей рассеяния мы можем только в том случае, если допустим, что в трансформаторе существует главный поток Ф, созданный н. с. обеих обмоток и сцепляющийся со всеми их витками. Такое допущение, очевидно, в большой степени оправдывается в применении к нормальным трансформаторам со стальным сердечником.

Мы можем теперь написать:

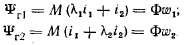Отсюда получаем:

Теория электрических машин также основана, как мы покажем в дальнейшем, на допущении существования главного потока, не зависящего от полей рассеяния.

Считая, что токи и э. д. с. уравнений (2-26)—(2-29) изменяются во вре-

мени по закону синуса, мы можем эти уравнения переписать в комплексной форме:

Ранее при рассмотрении режима холостого хода мы пренебрегали полем вне сердечника трансформатора. В действительности это поле согласно закону полного тока должно существовать. Оно называется полем рассеяния. Созданные им потокосцепления обмоток малы по сравнению с потокосцеплениями обмоток, созданными главным потоком, С большим приближением к действительным условиям можно считать, что поле рассеяния и поле в сердечнике, соответствующее главному потоку, существуют независимо одно от другого.

На рис. 2-13 представлена приближенная картина поля рассеяния, которую кладут в основу расчета потоко-сцеплений рассеяния. Здесь пунктирной линией показан путь главного потока Ф, сплошными линиями показаны индукционные линии поля рассея-

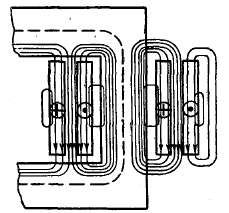Рис. 2-13. Приближенная картина поля рассеяния трансформатора с концентрическими обмотками. Крестиками и точками условно показаны направления токов в обмотках для рассматриваемого момента времени.

ния. Они могут быть условно разделены на две группы: сцепляющиеся с первичной обмоткой и сцепляющиеся со вторичной обмоткой. Магнитные сопротивления для потоков соответствующих индукционных трубок рассеяния определяются в основном сопротивлениями тех их частей, которые проходят вдоль обмоток и в промежутке между ними. Их можно принять постоянными, поскольку потоки трубок проходят по материалам (медь, изоляция, воздух или масло), для которых μ = const. Магнитными сопротивлениями потоков трубок вне обмоток и промежутка между ними можно пренебречь, так как здесь они проходят в основном по стали сердечника.

С учетом приведенных равенств (2-35) уравнения напряжений (2-24а) и (2-25а) для установившегося режима могут быть написаны в комплексной форме:

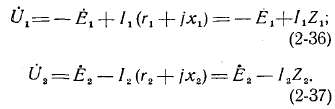Уравнения (2-36) и (2-37) называются векторными уравнениями напряжений трансформатора (здесь имеются в виду временные векторы напряжений, э. д. с. и токов).

В реальном трансформаторе со стальным сердечником при его работе возникают магнитные потери. Для их учета мы должны считать, так же как при холостом ходе, что ток I₀ имеет наряду с реактивной составляющей I_0р активную составляющую I_0а [см. уравнения (2-9)—(2-13)]; однако обе эти составляющие мы должны отнести не

Вследствие нелинейной связи между потоком Ф и результирующим током i₀ кривая последнего при синусоидальном потоке Ф будет несинусоидальной (§ 2-13). Для облегчения анализа зависимостей, характеризующих работу трансформатора, ток i₀ принимается синусоидальным с действующим значением, равным тому же значению действительного тока. Такое допущение не может привести к заметной ошибке из-за относительной малости тока I₀.

в) Приведение величин вторичной обмотки к числу витков первичной обмотки. Указанное приведение получим, если помножим уравнение (2-37) на отно-

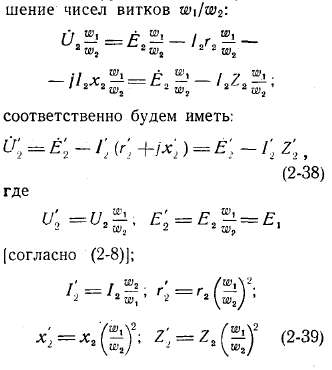представляют собой величины вторичной обмотки, приведенные к числу витков первичной обмотки. Такое приведение величин вторичной обмотки облегчает исследование работы трансформатора: делает более удобным построение для него векторных диаграмм (§ 2-4,г), позволяет построить удобную для расчетов схему соединения его активных и индуктивных сопротивлений, называемую схемой замещения трансформатора, где магнитная связь между обмотками заменена электрической связью между ними (§ 2-5).

Можно считать, что приведение величин вторичной обмотки к числу витков первичной обмотки сводится

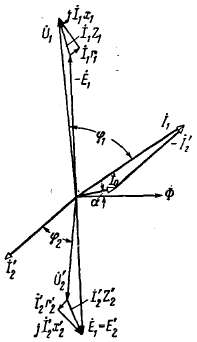Рис. 2-14. Векторная диаграмма трансформатора, работающего с отстающим током.

же найти соотношения между приведенными и действительными величинами вторичной обмотки. Они получаются такими же, как и (2-39).

г) Векторные диаграммы. Векторные диаграммы наглядно показывают соотношения между токами, э. д. с. и напряжениями обмоток. Они строятся в соответствии с уравнениями (2-19), (2-36) и (2-38).

На рис. 2-14 — 2-16 представлены диаграммы трансформатора, работающего с различными нагрузками.

Векторная диаграмма трансформатора, работающего, например, с отстающим током (рис. 2-14), при заданных

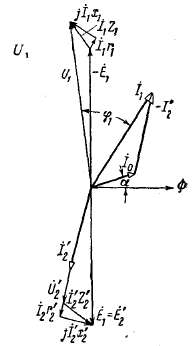Рис. 2-15. Векторная диаграмма трансформатора, работающего с cos φ₂=l.

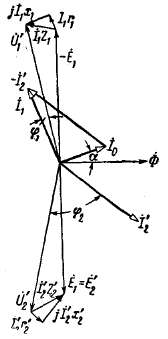
Рис. 2-16. Векторная диаграмма трансформатора, работающего с опережающим током.

Приведенные ранее уравнения напряжений и токов, а также векторные диаграммы относятся к однофазному трансформатору или к одной фазе трехфазного трансформатора. Различие токов холостого хода отдельных фаз трехфазного трансформатора вследствие несимметрии их магнитных

цепей не имеет практического значения, так как токи холостого хода составляют обычно небольшую долю номинального тока; параметры же отдельных фаз r₁, r'₂, x₁, x'₂ можно считать одинаковыми.

Содержание  Главная (библиотека)
Предыдущий § Следущий