Содержание
Предыдущий § Следующий

Глава третья ЯКОРНЫЕ ОБМОТКИ МАШИН ПОСТОЯННОГО ТОКА

§ 3-1. Общие сведения о якорных обмотках машин постоянного тока

Устройство обмоток

Обмотка якоря является важнейшим элементом машины и должна удовлетворять следующим требованиям:

1) обмотка должна быть рассчитана на заданные величины напряжения и тока нагрузки, соответствующие номинальной мощности;

2) обмотка должна иметь необходимую электрическую, механическую и термическую прочность, обеспечивающую достаточно продолжительный срок службы машины (до 15—20 лет);

3) конструкция обмотки должна обеспечить удовлетворительные условия токосъема с коллектора, без вредного искрения;

4) расход материала при заданных эксплуатационных показателях (к. п. д. и др.) должен быть минимальным;

5) технология изготовления обмотки должна быть по возможности простой.

В современных машинах постоянного тока якорная обмотка укладывается в пазах на внешней поверхности якоря. Такие обмотки называются барабанными. Обмотки якорей подразделяются на петлевые и волновые. Существуют также обмотки, которые представляют собой сочетание этих двух обмоток.

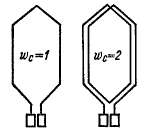
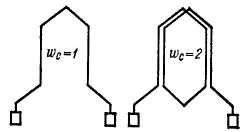
Основным элементом каждой обмотки якоря является секция, которая состоит из одного или некоторого количества последовательно соединенных витков и присоединена своими концами к коллекторным пластинам (рис. 3-1, 3-2).

В обмотке обычно все секции имеют одинаковое количество витков. На схемах обмоток секции для простоты изображаются всегда одновитковыми.

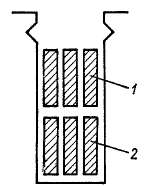
Для удобного расположения выходящих из пазов лобовых частей (см. рис. 1-9) обмотки якоря выполняются двухслойными. При этом в каждом пазу секции располагаются в два слоя (рис. 3-3): одна сторона каждой секции — в верхнем слое одного паза, а другая — в нижнем слое другого паза. На схемах обмоток стороны секций, находящиеся в верхнем слое, будем изображать сплош-

Рис. 3-1. Одновитковая и двухвитковая секции петлевой обмотки

Рис. 3-2. Одновитковая и двухвитковая секции волновой обмотки

ными линиями, а стороны, расположенные в нижнем слое, — штриховыми линиями (рис. 3-4). Однослойные якорные обмотки по принципу устройства не отличаются от двухслойных и применяются только при Р_н < 0,5 кет. Секции обмотки соединяются друг с другом в последовательную цепь (рис. 3-4) таким образом, что начало (н) последующей секции присоединяется вместе с концом (к) предыдущей секции к общей коллекторной пластине. Обмотки — петлевая и волновая — названы по внешнему очертанию контуров, образуемых последовательно соединенными секциями. Поскольку каждая секция имеет два конца и к каждой коллекторной пластине присоединены также два конца секций, то общее количество пластин коллектора К равно количеству секций обмотки S:

K = S.                        (3-1)

В простейшем случае в пазу находятся две секционные стороны: одна в верхнем и другая в нижнем слое. При этом число пазов якоря Z = S = К- Однако для уменьшения пульсаций выпрямленного тока и напряжения, а также во избежание возникновения чрезмерно большого напряжения между соседними коллекторными пластинами число пластин должно быть достаточно большим. Обычно при U_a = ПО -i- 220 в

К/2р = 12 4-35.

Рис. 3-3. Укладка обмотки в пазу

1 — сторона секции верхнего слоя; 2 — сторона секции нижнего слоя

С другой стороны, изготовление якорей с большим числом пазов нецелесообразно, так как при этом пазы будут узкими, значительная часть их площади будет занята изоляцией секций от корпуса, для проводников останется мало места и в итоге получится проигрыш в мощности машины. Кроме того, большой расход изоляционных материалов и увеличение штамповочных работ вызовут удорожание машины, а мелкие зубцы будут непрочными.

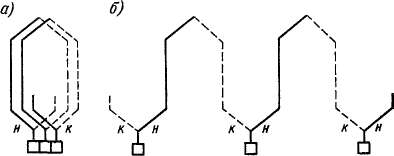Рис. 3-4. Соединение секций петлевой (а) и волновой (б) обмоток

По этим причинам обычно в каждом слое паза располагают рядом несколько (и_п = 2, 3, 4, 5) секционных сторон (на рис. 3-3 и_п = 2). При этом

К = 5 = u_nZ.                                        (3-2)

В данном случае говорят, что в каждом реальном пазу имеется «„элементарных пазов, так что в каждом слое элементарного паза имеется одна секционная сторона. Очевидно, что общее число элементарных пазов якоря

Z₃ = u_nZ = S = K. (3-3)

Когда и_п> 1, либо все секции имеют равную ширину (рис. 3-5, а), либо же часть секций имеет меньшую, а часть — большую

ширину (рис. 3-5, б). В первом случае обмотка называется р а в -посекционной, а во втором — ступенчатой. При ступенчатой обмотке условия токосъема с коллектора улучшаются (см. § 6-6), однако эта обмотка сложнее и дороже и поэтому применяется реже, притом только в машинах большой мощности (Р_а ж 500 кет и выше).

В равносекционных обмотках и_п секций, стороны которых лежат рядом в общих пазах, объединяются в катушку (рис. 3-6) и имеют

Рис. 3-5. Укладка секций равносекционной (а) и ступенчатой (б) обмоток при и_п = 2

общую изоляцию от стенок паза. Одновитковые секции при больших токах изготовляются из стержней, концы которых на противоположной от коллектора стороне якоря запаиваются с помощью хомутиков после укладки в пазы. Стержни и_П секций объединяются в полукатушку (рис. 3-7). Секции ступенчатой обмотки являются всегда стержневыми.

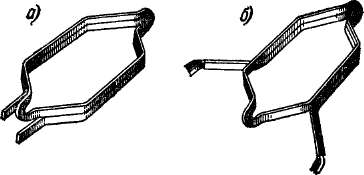Рис 3-6 Катушки петлевой (а) и волновой (б) обмоток

На рис. 3-8 приведены примеры выполнения изоляции пазовой части обмотки.

В машинах малой мощности, когда ток параллельной ветви не превышает 60—75 а, катушки изготовляются из круглых изолированных проводников. В этом случае пазы делают трапецевидными

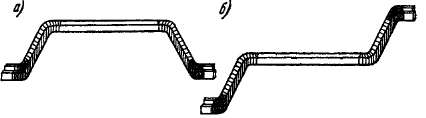Рис. 3-7. Полукатушки петлевой (а) и волновой (б) обмоток

(рис. 3-8, а), чтобы получить зубцы с неизменным по высоте сечением и тем самым избежать сильного насыщения корня зубца. Проводники катушки при этом опускаются в паз по одному через узкую щель открытия паза. Такие пазы называются полузакрытыми, и изоляция таких обмоток чаще всего выполняется класса А или Е. В случае применения проводников прямоугольного сечения паз также выполняется прямоугольным (рис. 3-8, б). Такие обмотки изготовляются с различными классами изоляции. При изоляции классов А и Е проводники обмотки могут также опускаться в паз по одном), и тогда ширина открытия паза равна примерно половине ширины паза. Такие пазы называются полуоткрытыми. При изоля-

ции классов В, F и Н заранее полностью изолированные катушки укладываются в полностью открытые пазы (рис. 3-8, б).

При D_a =s; 40 см и v_a ^ 35 м/сек обмотки в пазах укрепляются с помощью проволочных бандажей. Во всех остальных случаях

применяются клинья из твердых пород дерева (бук и др.), гетинакса, текстолита, стеклотекстолита и др.

Плотность тока в проводниках обмотки якоря при номинальной нагрузке находится в пределах 4—\0а/мм². Меньшая цифра относится к крупным машинам, большая — к малым.

Условия симметрии обмоток. В современных якорных обмотках соединенные последовательно друг с другом секции образуют замкнутую на себя цепь. Такую обмотку можно изобразить схематически в виде замкнутой спирали (рис. 3-9), по поверхности которой скользят щетки. В изображенном на рис. 3-9 простейшем случае обмотка имеет одну пару (а = 1) параллельных ветвей. В общем случае а = 1, 2, 3..., и тогда машину можно рассматривать состоящей из а параллельно работающих элементарных машин, каждая из которых имеет две параллельные ветви.

Для обеспечения наилучших условий работы машины необходимо, чтобы э. д. с. Е_а всех ветвей обмотки и их сопротивления были равны. В этом случае токи всех параллельных ветвей i_a также будут равны:

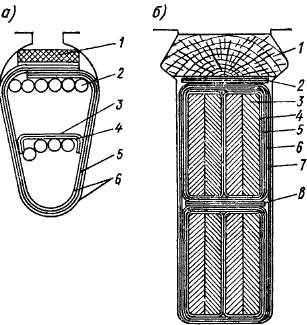Рис. 3-8. Пазовая изоляция класса А: а — полузакрытый паз

/ — клин гетинаксовый; 2 — изолированные проводники, 3 — прокладка из стеклолакоткани 0,18 мм; 4 — прокладка из электрокартона 0,2 мм; 5 — стекло-лакоткань эскапоновая 0,18 мм; 6 — электрокартон 0,2 мм

б — открытый паз

/ — клин деревянный, 2 — прокладка из электрокартона; 3 — изолированный проводник; 4 — мика-лента или синтетическая лента 0,13 мм; 5 — микафолий или синтетическая пленка 0,15 мм; 6 — телефонная бумага; 7 — электрокартон 0,2 мм; 8 — прокладка из электрокартона

Для удовлетворения этих условий необходимо, во-первых, чтобы магнитная цепь была симметричной по устройству и потоки всех полюсов были равны, во-вторых, чтобы все пары параллельных ветвей обмотки были эквивалентны, т. е. чтобы они располагались в магнитном поле идентичным образом. Обмотка, удовлетворяющая этим требованиям, называется симметричной.

При нарушении указанных требований разные ветви обмотки будут нагружаться различными по величине токами, что может

вызвать нарушение работы щеточных контактов, а кроме того, возрастут также потери в обмотке.

Чтобы обмотка была симметричной, на каждую пару параллельных ветвей должно приходиться одинаковое целое число (ц. ч.) секций и коллекторных пластин:

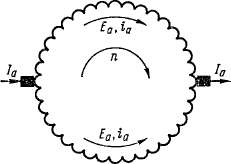Рис. 3-9. Цепь простейшей якорной обмотки

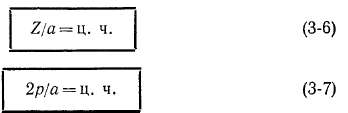
Для симметричного расположения параллельных ветвей в магнитном поле необходимо, чтобы

Соотношения (3-5), (3-6) и (3-7) представляют собой условия симметрии обмоток, и последние проектируются с их учетом. Однако в отдельных случаях допускаются определенные, не слишком большие отступления от этих требований, не вызывающие заметного ухудшения условий работы машины.

§ 3-2. Э. д. с. секций

Шаг секции. В дальнейшем будем представлять себе, что якорь разрезан по осевой плоскости и выпрямлен так, что пазы и обмотка якоря лежат в одной плоскости. Кроме того, будем предполагать, что такой развернутый якорь будет двигаться относительно неподвижных полюсов справа налево (рис. 3-10, а), а полюсы находятся перед плоскостью чертежа. При этом э. д. с. в проводниках обмотки

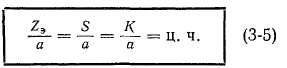
будут направлены под северными полюсами вниз, а под южными вверх.

Индуктируемая в секции э. д. с. максимальна, если ширина секции (или первый частичный шаг обмотки г/_х) равна полюсному делению т, так как при этом максимальное потокосцепление секции определяется полным потоком полюса в воздушном зазоре (рис. 3-10). В данном случае при любом положении вращающегося якоря стороны секции находятся под разноименными полюсами и в них индуктируются э. д. с. противоположных направлений, которые по контуру секции складываются.

Тем не менее, обычно обмотка выполняется с ух, несколько отличающимся от т, так как при этом величина э. д. с. существенным образом не изменяется, а условия токосъема с коллектора улучшаются (см. § 6-6). При ух = т. шаг называется полным или диаметральным, при г/1>т — удлиненным, а при г/₁<т — укороченным. Выполнения обмоток с удлиненным шагом обычно избегают, так как за счет удлинения лобовых частей в петлевых обмотках несколько увеличивается расход меди.

Шаг секции может быть выражен в пазовых или зубцовых делениях:

у_и=~±г_г,                                                                                                                                                            (3-8)

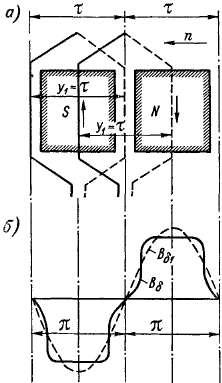Рис. 3-10.

где s_z < 1 представляет собой такую дробь, при которой y_lz будет целым числом. При е = 0 шаг является полным.

Шаг секции может быть определен также по элементарным пазам:

Очевидно, что при равносекционной обмотке у_г = u_ny_lz и е =

Звезда э. д. с. В секциях и во всей обмотке индуктируются переменные э. д. с. Как известно, синусоидальные э. д. с. могут быть изображены на векторных диаграммах в виде векторов. Для изучения свойств якорных обмоток машин постоянного тока также

Очевидно, что при равносекционной обмотке у_г = u_ny_lz и е =

Звезда э. д. с. В секциях и во всей обмотке индуктируются переменные э. д. с. Как известно, синусоидальные э. д. с. могут быть изображены на векторных диаграммах в виде векторов. Для изучения свойств якорных обмоток машин постоянного тока также

целесообразно пользоваться подобными векторными диаграммами. Однако при этом ввиду несинусоидальной формы э. д. с. проводников, витков и секций обмотки якорянеобходиморассматривать только основные гармоники этих э. д. с, т. е. первую гармонику кривой вида рис. 1-4, а.

В кривой поля под полюсами В_б (рис. 3-10, б) можно выделить первую, или основную, гармонику В^, период которой будет равен двойному полюсному делению 2т. Таким образом, в электромагнитном отношении дуга окружности машины, соответствующая 2т, равна 360 градусам, которые называются электрическими (360° эл.).

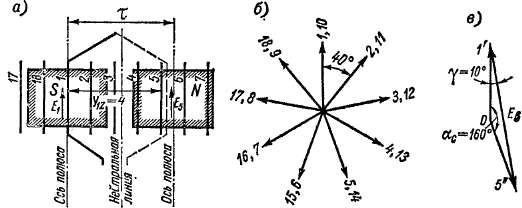Рис. 3-11. Схема (а), звезда э. д. с. пазов и секций (б) и векторная диаграмма э д. с. (в) обмотки с Z = Z_b = 18, 2р = 4

Очевидно, что полная окружность якоря, или геометрический угол 360°, соответствует электрическому углу р -360° эл.

Различные пазы якоря располагаются относительно основной гармоники поля полюсов различным образом, и поэтому основные гармоники э. д. с. проводников различных пазов будут сдвинуты по фазе. Угол сдвига между э. д. с. проводников соседних пазов

направлена вертикально вверх, и тогда в момент времени, изображенный на рис. 3-11, а, э. д. с. проводников пазов 1 и 10 имеют максимальное положительное значение.

Звезда пазовых э. д. с. имеет Z векторов, но отдельные векторы могут совпадать по фазе, и число лучей поэтому может быть меньше Z, так как при построении звезды и обходе векторов э. д. с. всех пазов совершается р полных оборотов. Если, например, Zip = ц. ч., то и число лучей равно этой величине, и диаграмма состоит из р совпадающих или накладывающихся друг на друга звезд.

Э. д. с. проводников витка и проводников двух сторон секции сдвинуты на угол

и векторы проводников секции, находящейся в пазах /и 1 +4 = = 5, будут взаимно расположены так, как показано на рис. 3-11, в.

На рис. 3-11, б, а также на всех последующих рисунках с одним штрихом обозначены векторы сторон секций, лежащих в верхнем слое паза, а с двумя штрихами — векторы сторон в нижнем слое.

При построении звезды (рис. 3-11, б) для э. д. с. проводников всех пазов было принято одинаковое положительное направление (например, снизу вверх на рис. 3-10, а). Поэтому по контуру витка э..д. с. двух его составляющих проводников вычитаются, и для случая, показанного на рис. 3-11, б, э. д. с. витка Е_в равна разности векторов Г и 5". В другом масштабе вектор Е_в на рис. 3-11, в представляет собой также э. д. с. секции Е_с.

Будем присваивать секции номер того паза, в котором она лежит своей верхней стороной.

Очевидно, что векторы э. д. с. двух секций, лежащих своими сторонами в соседних пазах, сдвинуты относительно друг друга на такой же угол а, как и э. д. с. проводников двух соседних пазов. Поэтому звезда э. д. с. секций аналогична звезде пазовых э. д. с. на рис. 3-11, б.

Применение векторных диаграмм для анализа свойств обмоток будет рассмотрено ниже.

Зубцовые пульсации э. д. с. Зубчатое строение якоря

способствует пульсации э. д. с. секций и э. д. с. обмотки в целом.

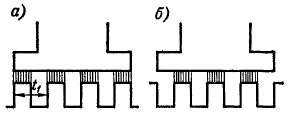
Если ширина полюсного наконечника не кратна зубцовому делению t_x (рис.'3-12, а и б), то магнитное сопротивление воздушного зазора между полюсом и якорем при повороте последнего меняется.

Рис. 3-12. Продольные пульсации маг нитного потока

Рис. 3-13. Поперечные пульсации магнитного потока

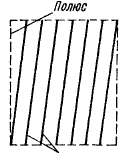
Пазы

Рис. 3-14. Скос пазов относительно полюсного наконечника

В результате возникают пульсации величин магнитного потока полюсов с частотой

f_g = Zn

и как следствие пульсации э. д. с. с такой же частотой в обмотке. Во избежание этого выбирают Zip равным нечетному числу. При этом сумма магнитных сопротивлений воздушных зазоров под двумя соседними полюсами при повороте якоря изменяться не будет и пульсации магнитного потока исчезнут.

Пульсации потока рассмотренного вида называются продольными. Кроме них, при движении якоря возникают также попереч-

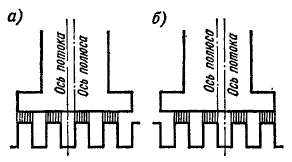
ные пульсации потока, выражающиеся в том, что ось магнитного потока полюсов в зазоре колеблется с частотой f_z около среднего положения (рис. 3-13, а и б). Вследствие этого потокосцепление обмотки и ее э. д. с. пульсируют с такой же частотой.

Эффективной мерой против влияния поперечных пульсаций потока является скос пазов относительно полюсного наконечника (рис. 3-14) или скос полюсного наконечника относительно оси машины при нескошенных пазах на якоре. Скос пазов производится на 0,5—1,0 зубцового деления и применяется в машинах мощностью до 30—40 кет. При скосе пазов снижается также шум машины.

§ 3-3. Простая петлевая обмотка

Шаги обмотки. На рис. 3-15 представлены два возможных варианта последовательного соединения секций простой петлевой обмотки. Эту обмотку называют также параллельной. На рис. 3-15 показаны шаги у_ъ у₂, у рассматриваемой обмотки, которые будем определять по элементарным пазам. Первый частичный шаг^ вычисляется по формуле (3-9) и определяет расстояние по поверхности якоря между начальной и конечной сторонами секции. Второй частичный шаг обмотки у_г определяет расстояние между конечной стороной данной секции и начальной стороной последующей за ней по схеме обмотки секции. Направление движения по якорю и коллектору вправо будем считать положительным. Так как в петлевой обмотке движение при переходе от конечной

стороны предыдущей секции к начальной стороне последующей совершается влево, то шаг у₂ в петлевой обмотке будем считать отрицательным числом. Результирующий шаг обмотки

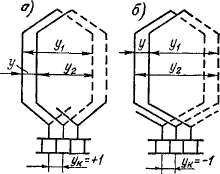Рис. 3-15. Секции неперекрещен-ной (а) и перекрещенной (б) простой петлевой обмотки

определяет расстояние между начальными сторонами данной и последующей за ней секцией.

Коллекторным делением называется ширина коллекторной пластины плюс ширина одной изоляционной прокладки между пластинами. Шаг по коллектору у_к определяет расстояние в коллекторных делениях между серединами коллекторных пла-

стин, к которым присоединены концы данной секции или, что то же самое, начала данной и последующей за ней секций. Очевидно,

Соотношения (3-9), (3-12) и (3-13) применимы для всех типов обмоток.

Отличительным свойством простой петлевой обмотки является то, что для нее

Знак плюс соответствует случаю |г/₂|>#1> и такие обмотки называются неперекрещенными (рис. 3-15, а). Знак ми-

Рис. 3-16. Таблица соединений секционных сторон простой петлевой обмотки, изображенной на рис. 3-17

нус соответствует случаю \у₂\> Уъ ^и такие обмотки называются перекрещенными (рис. 3-15, б). Во втором случае расход меди несколько больше, и поэтому выполнения таких петлевых обмоток избегают. В электромагнитном отношении эти обмотки равноценны и различаются только тем, что при той же полярности полюсов и том же направлении вращения полярности щеток противоположны.

Схема и основные свойства обмотки. Рассмотрим симметричную простую петлевую обмотку с данными:

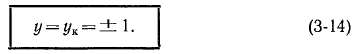
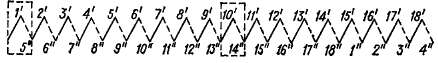
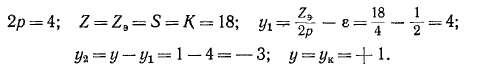
Будем присваивать секционным сторонам номера тех элементарных пазов, в которых они лежат. Тогда по известным значениям шагов можно составить таблицу соединений секционных сторон обмотки (рис. 3-16), исходя из определенного элементарного паза и прибавляя к номеру этого паза значение первого частичного шага, значение второго шага, затем опять первого и т. д. Номера верхних сторон секций, изображенных сплошными линиями, про-

ставлены в таблице на рис. 3-16 сверху, а номера нижних сторон секций, изображенных штриховыми линиями, — снизу. От нижней секционной стороны 4" (справа на рис. 3-16) по ходу обмотки вернемся опять к верхней стороне /', так как 4 + у_г = 4 — 3 = 1. Таким образом, обмотка является замкнутой.

По известным шагам или таблице соединений секционных сторон можно начертить также схему обмотки (рис. 3-17).

На рис. 3-17 проставлены номера элементарных пазов. Условимся, как это сделано на рис. 3-17, присваивать коллекторной

Рис. 3-17. Схема простой петлевой обмотки с 2р = 4, Z — 2_Э — S = К = 18, У\ = 4, у₂ = — 3, у = у_к = +1

пластине номер той секции, с началом которой соединена эта пластина.

Линия на поверхности якоря, проходящая в осевом направлении посередине между двумя соседними полюсами, называется линией геометрической нейтрали или геометрической нейтралью, так как вдоль этой линии магнитная индукция В = 0.

При вращении якоря некоторая часть секций, выделенных на рис. 3-17 жирными линиями, оказывается неизбежно замкнутой накоротко через щетки. Чтобы индуктируемые в этих секциях э. д. с. были минимальны и в секциях не возникало чрезмерных токов, которые вызовут перегрузку щеточных контактов, такие короткозамкнутые секции должны находиться на линии геометрической нейтрали или в ближайшей от этой линии нейтральной зоне. Для этого щетки устанавливаются так, чтобы в середине периода короткого замыкания стороны секции располагались симметрично

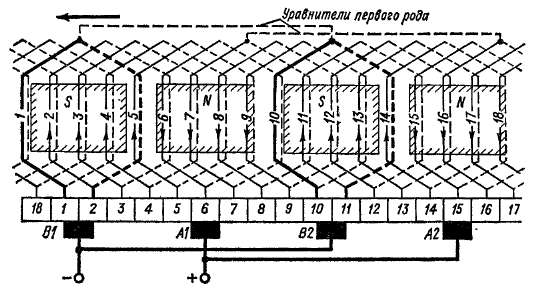
относительно середины полюса. Тогда говорят, что щетки установлены на нейтрали. При симметричной форме лобовых частей секций щетки расположены по осям полюсов (рис. 3-17).

Совершим обход цепи обмотки (рис. 3-17) слева направо, начиная с секции 2. Проходя последовательно, начиная от щетки 51, секции 2, 3, 4 а 5, мы мысленно движемся по направлению индуктируемых э. д. с. и выходим к щетке А1. Следовательно, эти секции составляют одну параллельную ветвь, э. д. с. которой равна сумме э. д. с. этих секций. Проходя затем от щетки А1 к щетке В2 по контуру секций 6, 7, 8, 9, мы обойдем вторую параллельную ветвь, двигаясь против направления индуктируемых э. д. с. Секция 10 замкнута накоротко. Секции 11, 12, 13 и 14, расположенные между щетками В2 и А2, составляют третью ветвь, а секции 15, 16, 17 и 18, расположенные между щетками А2 и В1, — четвертую ветвь. Обход этой последней ветви также совершается против направления э. д. с., причем после нее мы приходим к пластине /. Секция / также замкнута накоротко. Через каждую щетку простой петлевой обмотки протекают токи двух параллельных ветвей.

Верхние стороны секций каждой параллельной ветви находятся под одним полюсом, а нижние — под другим. На рис. 3-16 коротко-замкнутые секции обведены штриховыми прямоугольниками.

Таким образом, обмотка на рис. 3-17 имеет четыре параллельные ветви, а в общем случае простая петлевая обмотка содержит

параллельных ветвей, что является характерной особенностью этой обмотки. Очевидно, что условия симметрии (3-5), (3-6) и (3-7) для обмотки, изображенной на рис. 3-17, удовлетворяются.

Если машина работает в режиме генератора, стрелки на рис. 3-17 указывают также направление токов в обмотке. При этом полный ток якоря /„ тоже распределяется по четырем ветвям. В соответствии с изложенным цепь обмотки (рис. 3-17) можно изобразить упрощенно, как показано на рис. 3-18, где ветви обмотки и распределение тока выглядят более наглядно.

На основании рассмотрения рис. 3-17 можно установить также следующее. Если обмотка имеет полный шаг и щетки установлены на нейтрали, то э. д. с. ветви будет наибольшей. Кроме того, при этом направлении токов всех проводников, лежащих под одним полюсом, будут одинаковы, и поэтому развиваемый электромагнитный момент будет максимальным. Следовательно, такое устройство обмотки и такое расположение щеток являются наиболее выгодными. Небольшое отклонение шага у_г от полного не оказывает заметного влияния на величину э. д. с. и вращающего момента, так к#к изме-

нение направлений э. д. с. и токов при этом происходит только в таких проводниках параллельной ветви, которые располагаются вблизи нейтрали, т. е. в зоне слабого магнитного поля.

Расположение параллел-ьных ветвей в пространстве относительно неподвижных полюсов определяется положением щеток и также неизменно. При вращении якоря секции переходят попеременно из одной ветви в другую, причем во время такого перехода секция замыкается накоротко щеткой и в ней происходит изменение направления тока, например, от значения +i_a до значения —t_a. Это явление называется коммутацией секции. Явления в короткозамкнутой секции влияют, как уже указывалось, на величину токов в щеточном контакте и на работу щеток. Совокупность явлений, связанных с замыканием секций накоротко щетками, переходом этих секций из одних параллельных ветвей обмотки в другие и передачей тока через скользящий контакт между коллектором и щеткой, называется коммутацией машины. Подробно вопросы коммутации рассматриваются в гл. 6.

Векторная диаграмма э. д. с. обмотки. Пользуясь

рассмотренной в § 3-2 звездой э. д. с. секций, можно построить векторную диаграмму э. д. с. обмотки, складывая векторы э. д. с. секций в той последовательности, в какой секции расположены по контуру обмотки.

Такая диаграмма вместе со звездой э. д. с. секций для обмотки, показанной на рис, 3-17, изображена на рис. 3-19. Поскольку векторы э. д. с. соседних секций при Z = 18 и 2р = 4 сдвинуты на 40° (см. § 3-2), то после построения векторов девяти секций происходит поворот на 9 -40° = 360° и многоугольник э. д. с. замыкается. После обхода остальных девяти секций получается второй многоугольник, накладывающийся на первый.

Каждый многоугольник э. д. с. соответствует одной паре параллельных ветвей. В общем случае при простой петлевой обмотке получается р многоугольников, которые при полной идентичности всех пар параллельных ветвей накладываются друг на друга, что свидетельствует о симметрии обмотки.

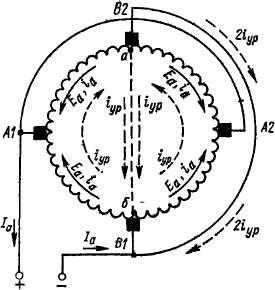Рис 3-18 Упрощенное представление цепи обмотки, показанной на рис. 3-17

Начала векторов /, 2, 3 ... на рис. 3-19 представляют собой потенциалы начал секций 1,2, 3 ..., а также потенциалы коллекторных пластин /, 2, 3... Совпадение концов и начал векторов обоих многоугольников на рис. 3-19 указывает на наличие в обмотке равнопотенциальных точек. Например, равные потенциалы имеют коллекторные пластины 1 и 10, 2 и 11 и т. д., т. е.

вообще пластины, удаленные друг

от друга на

Рис. 3-19. Векторная диаграмма

э. д. с. обмотки, показанной на

рис. 3-17

коллекторных делений. Такой вывод для симметричной обмотки вполне естествен, так как стороны секций, сдвинутых на у_П элементарных пазов, находятся под полюсами одинаковой полярности, в одинаковом магнитном поле. Величина у_п называется потенциальным шагом.

На диаграмме э. д. с. можно показать условно также щетки, как это сделано на рис. 3-19 для положения обмотки относительно щеток согласно рис. 3-17. Многоугольник э. д. с. надо представлять себе вращающимся, и сумма проекций векторов одной ветви или одной половины многоугольника на вертикальную ось щеток будет равна э. д. с. ветви и обмотки в целом. Величина этой э. д. с. пульсирует ' между значениями, которые соответствуют длинам двух штрих-пунктирных линий на рис. 3-19. Можно показать, что уже при К12р = 10 эти пульсации составляют менее 1 %. В действительности эти пульсации еще меньше вследствие того, что вблизи геометрической нейтрали индукция поля полюсов значительно меньше его основной гармоники.

Уравнительные соединения. В идеальных условиях, когда обмотка симметрична и потоки всех полюсов равны, э. д. с. всех ветвей также равны и ветви загружаются токами равномерно. Однако в действительности из-за производственных и иных отклонений (неодинаковая величина воздушного зазора под разными полюсами, неоднородность материалов сердечников и т. п.) потоки отдельных полюсов не будут в точности равны. При этом э. д. с. ветвей простой петлевой обмотки также не будут равны, так как

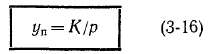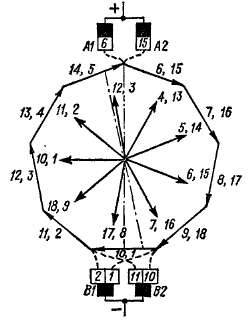
ветви сдвинуты относительно друг друга на одно полюсное деле-' ние (рис. 3-17).

Предположим, что на рис. 3-18 э. д. с. нижних ветвей больше, чем э. д. с. верхних ветвей. При этом уже при холостом ходе генератора, когда I_a = i_a = 0, внутри обмотки будут циркулировать уравнительные токи i_yp, которые замыкаются через щетки одинаковой полярности и соединительные провода или шины между ними. Так как внутреннее сопротивление обмотки мало, то эти токи могут быть значительными уже при небольшой разнице в потоках отдельных полюсов. При работе машины токи нагрузки щеток 2/„ будут алгебраически складываться с токами 2/_Ур, в результате чего щетки В1, В2 окажутся перегруженными, а щетки А1, А2 — недогруженными. Правильная работа щеток при этом может нарушиться. Еще более серьезное влияние на условия работы щеток оказывает нарушение баланса э. д. с. в короткозамкнутых секциях, вызванное уравнительными токами (см. § 6-6).

Для того чтобы разгрузить щетки от уравнительных токов и дать этим токам возможность замыкаться внутри самой обмотки, обмотка снабжается уравнительными соединениями, или уравнителями. Уравнители соединяют внутри обмотки точки, которые теоретически имеют равные потенциалы.

Как было установлено выше, эти точки сдвинуты на пару полюсов или при 2р = 4 на половину окружности якоря или коллектора. Одно уравнительное соединение показано на рис. 3-18 штриховой линией абпо вертикальному диаметру. Так как сопротивление щеточных контактов значительно больше сопротивления уравнительного провода, то токи t_yp замыкаются по этому проводу, минуя щетки, как показано на рис. 3-18. Такие соединения, применяемые в простых петлевых обмотках, называются уравнителями первого рода.

На векторных диаграммах при наличии равнопотенциальных точек концы или начала векторов соответствующих секций совпадают.

Уравнители выполняются либо на стороне коллектора (и тогда они соединяют пластины с равными потенциалами), либо на противоположной от коллектора стороне (и тогда они соединяют равно-потенциальные точки лобовых частей секций). Шаг уравнителей г/ур равен потенциальному шагу обмотки у_п:

При равенстве потоков полюсов токи в уравнителях не возникают. На рис. 3-17 штриховыми линиями показаны два уравнителя первого рода.

Для достижения надлежащего эффекта при всех положениях вращающегося якоря обмотку нужно снабдить достаточным количеством уравнителей. Из рассмотрения многоугольника э. д. с.

(рис. 3-19) видно, что максимальное число возможных уравнителей первого рода на одной стороне якоря равно Kip, причем каждый из них соединяет р точек равного потенциала. Полным количеством уравнителей снабжаются только крупные машины с тяжелыми условиями коммутации тока. В остальных случаях выполняют от ¹/_а до V_e всех возможных уравнителей или один уравнитель на один-два паза машины. При этом их размещают равномерно по окружности якоря. Сечение уравнителей берут равным 20—50% сечения витка обмотки якоря. На рис. 3-20

показан один из вариантов конструктивного выполнения уравнителей.

Протекающие по обмотке уравнительные токи являются переменными, и по правилу Ленца они создают магнитное поле, которое стремится устранить неравенство потоков полюсов. Поэтому

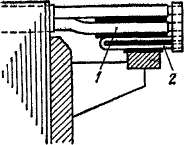
Рис. 3-20 -Уравнители (2), размещенные под лобовыми частями (/) на стороне якоря, противоположной коллектору

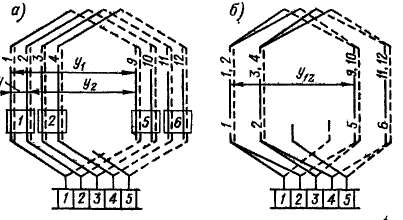
Рис. 3-21. Варианты изображений схемы равносекционной обмотки с 2р = 4, Z = 18, м_п = 2, Z₉ = S = /С == 36,

У\ = 8, & = — 8, у = у_к = +1

наличие уравнителей приводит также к значительному ослаблению уравнительных токов.

Простые петлевые обмотки с и_в > 1. Обмотка на рис. 3-17 имела 2р = 4, Z = Z₉ = S = /С = 18 и а_п = 1. Рассмотрим теперь об-мотку при тех же 2р = 4 и £ = 18, но м_п = 2 и Z, = 5 = К = 36.

Если при этом сохраним шаг по пазам у_1г = 4, то у_г — и_пу\_г = = 2-4 = 8, у_г = —7, у = у_к — +1. Эта обмотка будет равносек-ционной.

Схему такой обмотки можно изображать двояким образом, как показано на рис. 3-21, а я б. Верхний ряд цифр на этом рисунке представляет собой номера секций, а нижний ряд — номера пазов. Так как число пазов не изменилось, то и звезда пазовых э. д. с. не изменяется (см. рис. 3-11, б). Векторы э. д. с. каждой пары секций (1—2, 3—4 и т. д.) будут совпадать по фазе, а векторы э. д. с. секций, лежащих в соседних пазах (секции 2—3, 4—5 и т. д.), будут

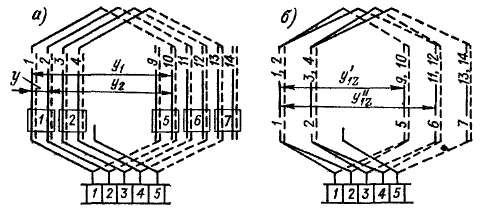
Рис. 3-22. Варианты изображения схемы ступенчатой обмотки с 2р= 4, Z = 18, и_п = 2, Z_B = S = К = 36, г/! = 9, й - -8, I/ = у_к = +1

сдвинуты на 40°, как и в предыдущем случае. Поэтому многоугольник э, д. с. обмотки будет выглядеть так же, как и на рис. 3-19, с тем лишь различием, что каждая сторона многоугольника будет представлять собой сумму э. д. с. двух секций, лежащих в общих пазах.

Если при тех же значениях 2р, Z и Z_s выбрать шаги по элементарным пазам

то обмотка будет ступенчатой. Схема такой обмотки также может быть изображена двояким образом, как показано на рис. 3-22, аи б. При этом обмотка имеет два значения шага у_1г ло зубцам; у'_1г = 4 и у[г = 5.

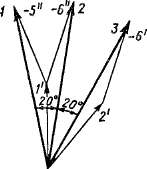
Построим векторы э. д. с. секций /, 2, 3 этой обмотки (рис. 3-23). Секция / лежит в пазах / и 5, и ее э. д. с. равна разности векторов / и 5 звезды на рис. 3-1*1, б. Построенный таким образом вектор секции 1 на рис. 3-23 обозначен /, а составляющие его векторы пазов или секционных сторон обозначены /' и —5". Секция 2 лежит в пазах /

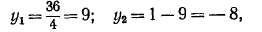
О

Рис. 3-23. Векторы э. д. с. секций обмотки, показанной на рис. 3-22

и б, а секция 3 — в пазах 2 и 6, и векторы э. д. с. этих секций построены и обозначены на рис. 3-23 по такому же принципу, как и вектор секции /. Как следует из этого рисунка, векторы э. д. с. секций сдвинуты относительно друг друга на 20°, т. е. на половину угла, соответствующего пазовому делению. Таким образом, ступенчатая обмотка с Z = 18 и Z_b = 36 в этом отношении равноценна обмотке с удвоенным числом пазов Z = Z₃ = 36. Соответственно этому многоугольник э. д. с. ступенчатой обмотки будет иметь в два раза больше сторон и в большей мере приближаться к окружности, чем при равносекцион-ной обмотке. Это является некоторым преимуществом ступенчатой обмотки. Однако главное преимущество такой обмотки состоит в улучшении условий коммутации (см. § 6-6). Уравнители первого рода для рассмотренных равносекционной и ступенчатой обмоток выполняются так же просто, как и в ранее рассмотренном случае. Разница заключается лишь в том, что вследствие удвоения S = К шаг уравнителей г/_ур также удваивается.

Аналогично схемам на рис. 3-21 и 3-22 можно изображать также схемы и других типов обмоток при и_П > 1.

§ 3-4. Сложная петлевая обмотка

Общие положения. Сложную, или многоходовую, петлевую обмотку можно рассматривать как сочетание нескольких (пг = 2, 3...) простых петлевых обмоток. Такую обмотку называют также сложной параллельной. В рассматриваемой обмотке секции и коллекторные пластины m простых обмоток по окружности чередуются и для отвода тока из обмотки необходимо, чтобы ширина щеток была не меньше m коллекторных делений. Таким образом, m простых обмоток m-ходовой обмотки включаются с помощью щеток параллельно и количество параллельных ветвей сложной петлевой обмотки

2а = 2pm.                                                                                                                                                                                                                                                                                                                                                                                                                                                                                      (3-18)

Результирующий шаг по элементарным пазам и шаг по коллектору сложной петлевой обмотки

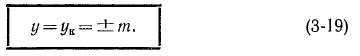
Шаги у_х и у_% = у — у_х определяются так же, как и для простой петлевой обмотки.

Сложная петлевая обмотка применяется в мощных машинах с большими токами якоря, и секции обмотки в этом случае являются одновитковыми.

Симметричная двухходовая двукратнозамкнутая петлевая обмотка. Рассмотрим особенности сложной петлевой обмотки на конкретном примере: m — 2, 2р = 4, Z = Z_b = S = К = 20, и_а = 1.

Рис. 3-24. Таблица соединений секционных сторон сложной петлевой обмотки, показанной на рис. 3-25

При этом 2а = 4 >2 = 8 и условия симметрии (3-5)—(3-7) соблюдаются. Заметим, что эти условия в сложной петлевой обмотке при т = 2 соблюдаются всегда, если К1р равно четному числу. Выберем шаги обмотки:

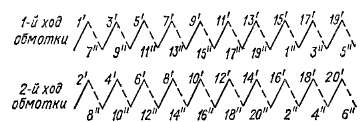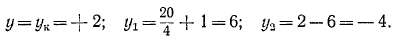По известным значениям шагов построим таблицу соединений секционных сторон обмотки (рис. 3-24). При этом, начиная с пластины и секции /, обойдем все нечетные секции и вернемся к пластине 1, замкнув первый ход обмотки. Начав второй ход с пластины 2, обойдем все четные секции и снова вернемся к пластине 2, замкнув второй ход обмотки.

Таким образом, в рассматриваемом случае получаются две самостоятельные обмотки, которые соединяются параллельно с помощью щеток. Это обусловлено тем, что S = К является в данном случае четным числом. Такая обмотка называется двукратнозамкну-той. В общем случае кратность замыкания сложной петлевой обмотки t равна общему наибольшему делителю чисел т и К-

Схема рассматриваемой обмотки представлена на рис. 3-25.

На рис. 3-26 изображена звезда э. д. с. пазов или сторон секций, в которой векторы сдвинуты на угол

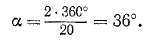
Построим в данном случае не векторную диаграмму э. д. с. секций, а диаграмму э. д. с. секционных сторон. Для этого будем складывать последовательно по ходу обмотки, согласно рйс. 3-24, э. д. с. секционных сторон. Так как по ходу обмотки э. д. с. нижних сторон секций вычитаются, они складываются с обратным знаком. В результате получим многоугольник э. д. с. (рис. 3-26), который состоит из четырех накладывающихся друг на друга многоу-

гольников, что. также указывает на наличие в обмотке восьми параллельных ветвей.

Уравнительные соединения. Для обеспечения равномерного распределения тока между ветвями каждого хода обмотки, показанной на рис. 3-25, следует выполнить рассмотренные в § 3-3 уравнители первого рода. Их шаг

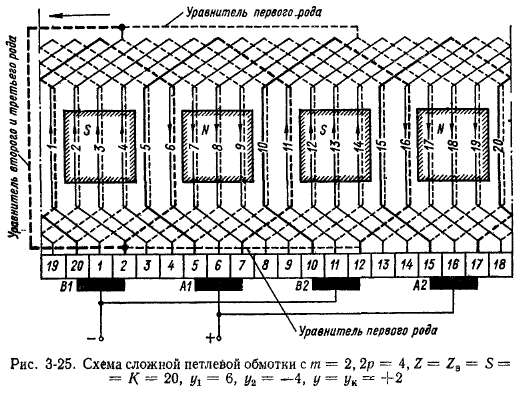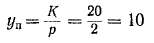является четным числом, и поэтому каждый уравнитель первого рода действительно будет соединять только пластины и секции одного хода обмотки (рис. 3-25).

Вместе с тем сложная петлевая обмотка нуждается также в так называемых уравнителях второго рода, которые

служат для выравнивания нагрузки между разными ходами сложной обмотки.

Каждая щетка (рис. 3-25) касается пластин разных ходов обмотки. Щеточный контакт не может быть вполне устойчивым, так как отдельные пластины несколько выступают по отношению к соседним и т. д. Поэтому условия контакта с пластинами разных ходов постоянно изменяются, что вызывает беспрерывное перераспределение тока нагрузки и пульсацию токов отдельных ходов об-

Рис. 3-26. Векторная диаграмма э. д. с. обмотки, изображенной на prfc. 3-25

мотки. Вместе с тем сильно колеблются также напряжения между соседними пластинами. Все это приводит к перегрузке отдельных участков щеток, их искрению и т. д.

Во избежание таких явлений необходимо соединить теоретически равнопотенциальные точки разных ходов обмотки уравнителями второго рода и таким образом осуществить их параллельное соединение внутри самой обмотки помимо или до щеточного контакта.

Как уже указывалось, две равнопотенциальные точки рассматриваемой обмотки удалены на одной стороне якоря на у_а = 10 пластин или элементарных пазов и принадлежат поэтому одному ходу обмотки. Вследствие этого в данном случае выполнение уравнителей второго рода на одной стороне якоря невозможно.

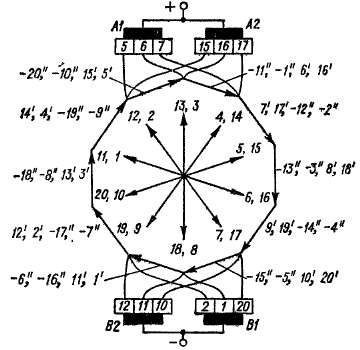
Из рассмотрения рис. 3-26 видно, что две равнопотенциальные точки разных ходов обмотки будут, например, соответствовать концу вектора /' (или началу вектора — 7") и началу вектора 2'. Это будут соответственно середина лобовой части секции / на стороне, противоположной коллектору, и коллекторная пластина 2. Эти две равнопотенциальные точки (рис. 3-25), а также другие аналогичные пары точек можно соединить уравнителями второго рода, проходящими между сердечником якоря и валом машины. В данном случае уравнители первого рода, принадлежащие разным ходам обмотки, выполняются на разных сторонах якоря, как показано на рис. 3-25, так как при этом р уравнителей второго рода можно заменить одним. Например, показанный на рис. 3-25 уравнитель второго рода для секций / и 2 служит также уравнителем второго рода для середины секции // и начала секции 12. В таком случае обычно выполняют только один уравнитель второго рода на (2 .+■ -г- 3) р коллекторных пластин. Недостатком уравнителей, проходящих между сердечником якоря и валом, является их конструктивная сложность.

Иногда в машинах с тяжелыми условиями коммутации в двухходовых петлевых обмотках применяют также уравнители третьего рода. Их задача сводится к тому, чтобы при вращении коллектора щетка замыкала накоротко не сразу всю секцию, а сначала одну ее половину и затем другую.

Для этого необходимо середину одновитковой секции, расположенной на противоположной от коллектора стороне якоря, соединить с коллекторной пластиной, находящейся между началом и концом данной секции. В обмотке, показанной на рис. 3-25, такую роль выполняют уравнители второго роДа, т. е. они являются также одновременно уравнителями третьего рода. Как видно из рис. 3-25, при движении коллектора вправо щетка В1 сначала замкнет пластины /—2 и тем самым левую половину секции 1, а затем пластины 2—3 и тем самым правую половину секции 1.

Уравнители третьего рода выполняют в таком количестве, чтобы коммутация всей обмотки происходила по полусекциям. Естественно, что уравнители третьего рода можно выполнять лишь в том случае, если соединяемые ими точки обмотки имеют равные потенциалы,

Несимметричные сложные петлевые обмотки. Рассмотрим двухходовую петлевую обмотку со следующими данными: m = 2, 2р = = 4, 2а = 8, Z = Z₃ = 5 = К = 18, у = у_к = +2, у_х = 4, у₂ = = —2. Так как К. — четное число, обмотка будет двукратнозамкну-той. Однако она не будет симметричной, так как условия (3-5) и (3-6) не выполняются. Заметим, что при m = 2 эти условия не выполняются, если К1р равно нечетному числу.

Последовательность соединений секций в этой обмотке представлена на рис. 3-27, а схема обмотки — на рис. 3-28.

Звезда э. д. с. секций и диаграмма э. д. с. рассматриваемой обмотки, построенные на основании рис. 3-27 и 3-28, изображены на рис. 3-29. При этом масштаб звезды э. д. с. в два раза меньше масштаба многоугольника э. д. с. То обстоятельство, что многоугольники э. д. с. на рис. 3-29 не совмещаются, также свидетельствует о несимметрии обмотки.

Равнопотенциальные точки этой обмотки имеют шаг

У^п==~р ⁼ Т ⁼ '

что следует также из рис. 3-29. Эти точки принадлежат разным ходам обмотки, и поэтому при соединении их получим уравнители второго рода, которые в данном случае располагаются на одной стороне якоря (рис. 3-28).

Но эти уравнители соединяют также параллельные ветви, находящиеся под разными парами ПОЛЮСОВ, И поэтому Рис. 3-27. Таблица соединений секционных сто-одновременно являются Р°н сложной петлевой обмотки, изображенной также уравнителями                                                                                                                                                                                                                                                                                                                                                               ^{на рис}' ³'²⁸

первого рода. То обстоятельство, что эти ветви принадлежат разным ходам обмотки, не имеет значения, так как при достаточном количестве уравнителей все ветви, расположенные под разными полюсами, окажутся взаимно соединенными друг с другом и щетки будут загружаться равномерно.

Простота выполнения уравнителей первого и второго рода является большим преимуществом рассматриваемой обмотки, и поэтому несимметричные двухходовые обмотки с К/р, равным нечетному числу, на практике часто предпочитают симметричным с К/р, равным четному числу.

Предположим, что в обмотке, показанной на рис. 3-28, желательно выполнить также уравнители третьего рода, один из которых можно было бы провести между точками а и б на рис. 3-28. На рис. 3-30, а построен вектор э. д. с. секции / этой обмотки, а на рис. 3-29 з. д. с. секции. 1 представлена штриховой линией также в виде разности э. д. с. проводников витка. При этом из рис. 3-29 видно, что точки а и б на рис. 3-28 не являются равно потенциальными и выполнить уравнители третьего рода невозможно. Если бы на схеме рис. 3-28 был взят удлиненный шаг г/i = 5, то потенциал точки а сместился бы в противоположную сторону (рис. 3-30, б).

Рис. 3-27. Таблица соединений секционных сторон сложной петлевой обмотки, изображенной на рис. 3-28

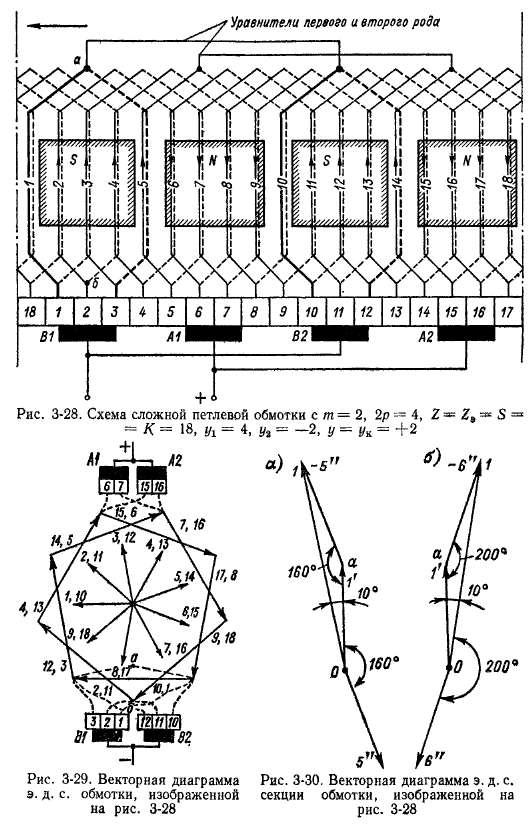
Однако и в этом случае точки а и б были бы неравнопотенциальными. Поэтому при необходимости выполнения уравнителей третьего рода применяют симметричные двухходовые обмотки типа показанной на рис. 3-25 с Kip, равным четному числу.

При нечетном К двухходовая петлевая обмотка будет однократ-нозамкнутой, но такая обмотка будет во всех случаях несимметричной, так как а = 2р является четным числом и условие (3-5) не выполняется. Трехходовые петлевые обмотки (ш = 3, а = Зр) будут тоже всегда несимметричными, так как не выполняется условие (3-7). Тем не менее в последнее время обмотки с m = 3 используются в мощных машинах.

Для несимметричных обмоток всегда требуется анализ возможности их применения. Эти вопросы, а также особенности выполнения многоходовых обмоток с м_п > 1 и ступенчатых обмоток рассматриваются в специальных руководствах [12, 30, 40, 41].

§ 3-5. Простая волновая обмотка

Общие положения. Мысленно обходя последовательно соединенные секции простой волновой обмотки, мы совершаем волнообразный обход якоря, причем каждый обход включает р секций и заканчивается на коллекторной пластине, которая находится слева или справа рядом с исходной (рис. 3-31). В первом случае (рис. 3-31, а) получается неперекрещенная обмотка, а во втором (рис. 3-31, б) —перекрещенная. Во втором случае расход меди будет несколько больше. Рассматриваемую обмотку называют также простой последовательной обмоткой.

В соответствии со сказанным между шагом по "коллектору у_к (рис. 3-31) и количеством коллекторных пластин К простой волновой обмотки существует зависимость

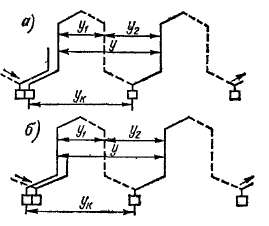Рис. 3-31. Секции неперекрещенной (а)

и перекрещенной (б) простой волновой

обмотки

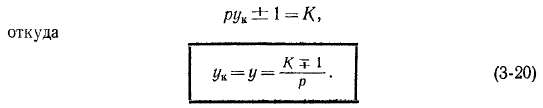
Знак минус относится к неперекрещенной обмотке, а знак плюс — к перекрещенной. Поскольку шаг у_к = у должен быть целым числом, то К не может принимать произвольных значений.

Шаг у₁ определяется по формуле (3-9), и

Шаги у₁ и у₂ близки к т, а у = у_к — к 2т.

Симметричная волновая обмотка. Ознакомимся со свойствами простой волновой обмотки на примере обмотки c2p = 4nZ = Z₃ = = S = К — 17. Возьмем при этом

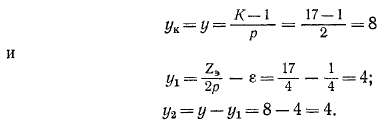Порядок соединений секционных сторон обмотки определяется таблицей на рис. 3-32, а схема обмотки имеет вид, показанный на

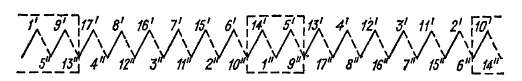Рис. 3-32. Таблица соединений секционных сторон простой волновой обмотки, показанной на рис. 3-33

рис. 3-33. Ряд секций, выделенных на рис. 3-33 жирными линиями, в отличие от секций петлевых обмоток замыкается накоротко через две щетки одной полярности и соединительные провода между ними. Короткозамкнутые секции обведены рамкой также и на рис. 3-32.

На рис. 3-34 построена звезда э. д. с. секций и векторная диаграмма э. д. £.. обмотки, представленной на рис. 3-33. Масштаб звезды э. д. с. в два раза больше масштаба многоугольника э. д. с.

Как следует из рис. 3-32, 3-33 и 3-34, обмотка имеет две параллельные ветви. Одна из них содержит секции 17, 8, 16, 7, 15, 6, присоединена своими концами к коллекторным пластинам 17, 14 и расположена, таким образом, между щетками А2, В2. Другая ветвь содержит секции 13, 4, 12, 3, 11, 2, присоединена концами к пластинам 13, 10 и расположена между щетками В2, А1,

Полученный вывод носит общий характер: всякая простая волновая обмотка имеет число параллельных ветвей

и векторная диаграмма э. д. с. такой обмотки всегда состоит из одного многоугольника.

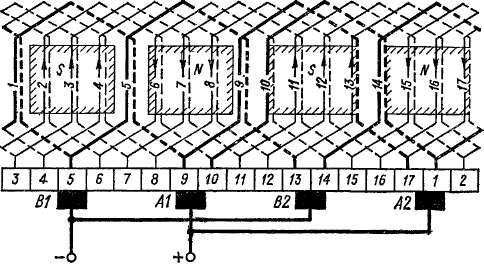Рис 3-33. Схема простой волновой обмотки с 2р = 4, Z = Z_b= S = = К = 17, & = 4, & = 4, {/_к = 8

Поскольку каждая из ветвей простой волновой обмотки проходит под всеми полюсами, то неравенство потоков полюсов не вызывает неравенства э. д. с. и токов параллельных ветвей. Поэтому такая обмотка не нуждается в уравнительных соединениях.

Более того, согласно выражениям (3-16) и (3-20), шаг у_п в простой волновой обмотке является не целым числом и поэтому равнопотенциальных точек не имеется, что видно также из рис. 3-34.

При волновой обмотке на коллекторе можно установить только два щеточных пальца, например А1 и В2 на рис. 3-33, так как все щетки данной полярности соединены короткозамкнутыми секциями, через которые ток нагрузки распределяется по параллельно работающим щеткам каждой полярности. Два щеточных пальца примут на себя весь ток нагрузки, и короткозамкнутых секций не будет,

Эта возможность иногда используется в машинах мощностью до 0,5 кет, если доступ для ухода за щетками по всей окружности коллектора затруднен. Однако условия коммутации при этом ухудшаются. Кроме того, в более мощных машинах возникает необходимость удлинять коллектор. Поэтому обычно ставится полный комплект (2р) щеточных пальцев. При а = 1 условия симметрии (3-5), (3-6) и (3-7) удовлетворяются при любых р, Z, и_П и К- Однако возможности выбора этих величин ограничиваются соотношением (3-20), которое при подстановке К = u_nZ принимает вид

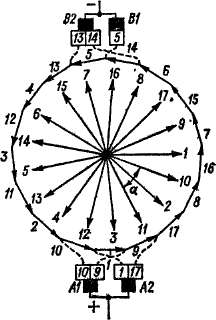Поскольку шаг у_к должен быть целым числом, то отсюда видно, что, например, при четных р как Z, так и и„ должны быть нечетными (и_п = 1, 3, 5...).

Простая волновая обмотка с мертвой секцией. Трудности в соблюдении равенства (3-20) или (3-23) в ряде случаев обходят, используя несимметричные обмотки. Например, при четных р и Z₃ = u_nZ можно применить обмотку с К = Z₃ — 1 и оставить одну секцию неиспользованной, или «мертвой». У этой секции обрезаются концы,

и она не присоединяется к коллектору (секция оставляется на якоре, чтобы

не нарушать балансировки).

Схема такой обмотки для 2р = 4, Z₃ = 16 и К = 15 показана на рис. 3-35,

причем принято, что

Рис. 3-34. Векторная диаграмма э. д. с. обмотки, изображенной на рис. 3-33

При обходе обмотки и счете шагов стороны мертвой секции исключаются.

Искусственно замкнутая простая волновая обмотка. Предположим, что Z₃= S = К = 16 и 2р = 4. Шаги обмотки выберем из предположения, что Z₃, S и К на единицу больше, т. е. Z₃ = S = К — 17. При этом, согласно выражению (3-20), можно взять

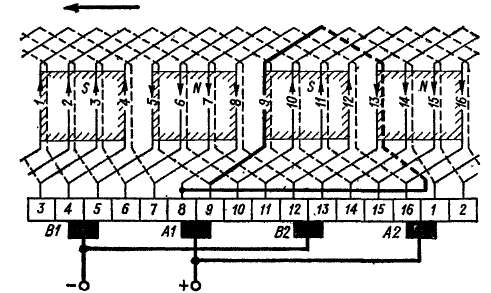
Исходя из таких значений шагов, составляем схему обмотки (рис. 3-36), начиная, например, с пластины 1. При первом обходе вокруг якоря проходим секции /и1+8=9и должны были бы прийти к пластине 9 + 8 = 17. Второй обход должен был бы включать в себя секции 17 и 8. Однако, поскольку секции 17 и пластины 17 нет, то после завершения первого обхода конец секции 9 с помощью

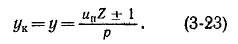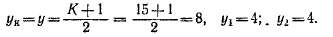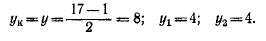
обходной перемычки непосредственно соединяем е пластиной 8 и началом секции 8. После этого ход обмотки следует по обычным правилам с тем лишь отличием, что каждый второй результирующий шаг сокращается на единицу.

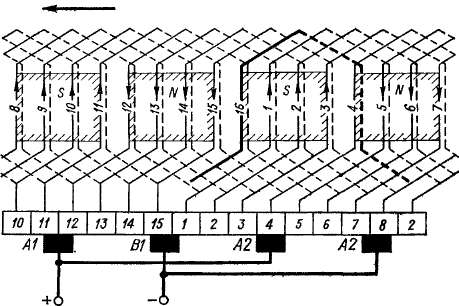Рис. 3-35. Схема лростой волновой обмотки с мертвой секцией с 2р = 4, Z= Z₃ = 16, у_г = 4, у₂ = 4, у_к = 8

Рис. 3-36. Схема искусственно замкнутой простой волновой обмотки с 2р = 4, Z = Z₃ == S = К = 16, у,, = 4, _й = 4, у_к = 8

Рассмотренные несимметричные волновые обмотки находят применение в машинах мощностью до нескольких десятков киловатт и работают вполне удовлетворительно.

§ 3-6. Сложная волновая обмотка

Общие положения. Сложную волновую обмотку можно рассматривать как сочетание m простых волновых обмоток, которые включаются на параллельную работу с помощью щеток. Число параллельных ветвей такой обмотки соответственно в m раз больше числа ветвей простой волновой обмотки:

Рассматриваемую обмотку называют также сложной последовательной обмоткой.

Согласно соотношениям (3-7) и (3-24), выполнение симметричных m-ходовых волновых обмоток возможно при условии

Шаги ух и у_г = у — у_х определяются обычным образом. Кратность замыкания обмотки равна общему наибольшему делителю чисел т и К.

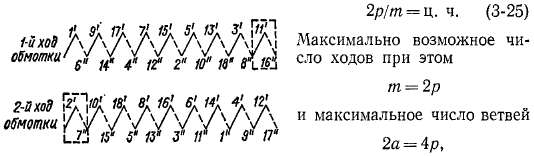
Рис. 3-37. Таблица соединений секционных сторон сложной волновой обмотки, изображенной на рис. 3-38

т. е. такое же, как у двухходовой петлевой обмотки. Секции и коллекторные пластины т ходов обмотки по

окружности чередуются. Поэтому после одного обхода р последовательно соединенных секций вокруг якоря мы должны выйти не к соседней с исходной пластине коллектора, как при простой волновой обмотке, а со сдвигом на т делений влево или вправо, В соответствии с этим

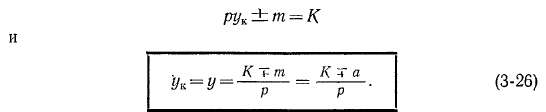
Рассмотрим двухходовую двукратнозамкнутую обмотку со следующими данными: 2р = 4, /и = 2, 2а = 4, Z = Z₃ = 5 = К = = 18. Условия симметрии (3-5)—(3-7) при этом удовлетворяются.

Выберем шаги:

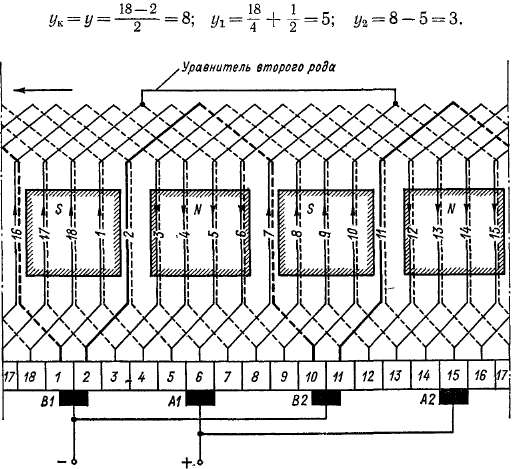Рис. 3-38. Схема двухходовой двукратнозамкнутой волновой обмотки с m = 2, 2р = 4, Z = Z_a = S = К = 18, у_х = 5, % = 3, у = г/_к = 8

На основании этих данных составлена таблица соединений секционных сторон обмотки (рис. 3-37) и схема обмотки (рис. 3-38). ОбмЪтка состоит из не связанных между собой двух простых волновых обмоток, из которых одна охватывает нечетные секции и пластины, а другая — четные. На основании рис. 3-37 и схемы рис. 3-38 на рис. 3-39 изображена звезда пазовых э. д. с. и векторная диаграмма э. д. с. обмотки. Диаграмма состоит из двух накладывающихся друг на друга многоугольников.

Уравнительные соединения

Для равномерной нагрузки отдельных ходов сложной волновой обмотки ее нужно снабдить уравнителями второго рода.

В рассмотренных выше случаях равнопотенциальный шаг

соответствует сдвигу по коллектору на два полюсных деления. Однако в сложных волновых обмотках Юр, согласно соотношению (3-26), может не равняться целому числу коллекторных делений. Поэтому в общем случае сложной волновой обмотки ближайшие равнопотенциальные коллекторные пластины могут отстоять друг

от друга на п = 1, 2, 3... пар по-люсных делений. При этом

где п — такое целое число, при котором у_а также является целым числом.

Умножив выражение (3-26) на п, можно заметить, что у_а [см. формулу (3-27)] может быть целым числом при таком наименьшем п, когда

Согласно формуле (3-27), при соблюдении условия (3-28) равно-потенциальный шаг сложной волновой обмотки

у_а = К/а. (3-29)

Расположение уравнителей второго рода на одной стороне машины возможно только при соблюдении условия (3*28). При и_п > > 1 требуется также соблюдение условия

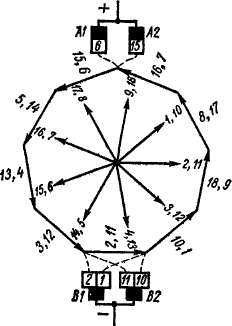
Рис 3-39. Векторная диаграмма

э д с. обмотки, изображенной на

рис. 3-38

что следует также из диаграммы э. д. с. на рис. 3-39. На рис. 3-38 показан один уравнитель второго рода.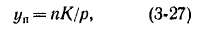

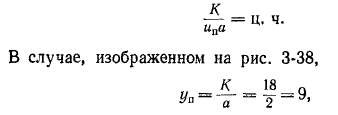
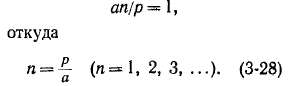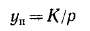
Применяются также обмотки ср = 3иа — 2, для которых условие (3-28) не соблюдается. В этом случае уравнители второю рода располагаются своими концами на разных сторонах якоря и проходят между валом и сердечником якоря,

§ 3-7. Комбинированная обмотка

Комбинированная, или лягушечья, обмотка впервые была предложена Латуром в 1910 г. и представляет собой сочетание петлевой и волновой обмоток, которые расположены в общих пазах, присоединяются к общему коллектору и работают параллельно.

Так как каждая из обмоток двухслойная, то в пазу располагаются четыре слоя обмотки. Каждая из обмоток рассчитывается на половину общего тока, и их э. д. с. должны быть равны. Таким образом, каждая обмотка рассчитывается на половину мощности машины.

Рассмотрим условия выполнения симметричной комбинированной обмотки при минимально возможном числе ветвей. Величины, относящиеся к петлевой и волновой обмоткам, будем при этом писать соответственно с индексом «го и «в».

Минимальное число ветвей имеет простая петлевая обмотка. Тогда т_ш = 1, а_а =*= р и, согласно соотношению (3-5),

/(/р = Ц. ч. При этом на основании формулы (3-26) должно быть

Следовательно, минимальное число ветвей волновой обмотки а_в = fn_B = p =

— «п-

Таким образом, петлевая и волновая обмотки должны иметь равные числа параллельных ветвей. Чтобы э. д. с. ветвей были равны, должны быть равны также числа витков ветвей обеих обмоток, а следовательно, и общее число проводников в Каждой обмотке. Из условия равенства токов следует, что сечения проводников обеих обмоток также должны быть одинаковы.

Поскольку при т_п > 2 петлевая обмотка уже не является симметричной, то возможны только два варианта симметричной комбинированной обмотки: \)т_п= 1, т_в = р; 2) т_а — 2, т_в = 2р.

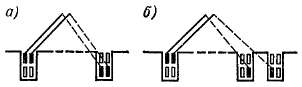
Так как петлевая и волновая обмотки присоединяются к общим коллекторным пластинам, то необходимо иметь определенные соотношения между шагами обмоток, чтобы не возникали уравнительные токи. Существуют два варианта этих соотношений (рис. 3-40).

В схеме Латура, изображенной на рис. 3-40, а,

Уы+У1в=~К/Р-> Ук.п+Ук.в^К/Р-                                                                                                                                                                                                                                                                                               (3-30)

Для предотвращения возникновения уравнительных токов в схеме рис. 3-40, а э. д. с. в контуре абвгдежз, замкнутом через щетки и соединительную шину между ними, должна равняться нулю. Это условие соблюдается, так как проводники де и гв лежат в одном пазу и имеют разные по величине и направлению э. д. с, а проводники аб и зж также имеют равные по величине и направлению э. д. с, поскольку они сдвинуты в магнитном поле на два полюсных деления.

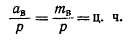
Схему Латура—Перре (рис. 3-40, б) можно получить из схемы Латура (рис. 3-40, а), если в последней шаги у_1п и у_1в являются полными:

и если проводники гв и зж перенести влево на одно зубцовое деление, т. е. укоротить шаги у_1п и y_ls на одно зубцовое деление. Очевидно, что при этом сумма 9j д. с. в контуре абвгдежз также будет равна нулю.

Для схемы рис. 3-40, б существуют следующие соотношения между шагами:

2/lB = 2/lm Ук. п + 5/к. в — К/р. (3-31)

Потенциальный шаг на коллекторе

Если выполнить на коллекторе уравнительные соединения с таким шагом, то они будут

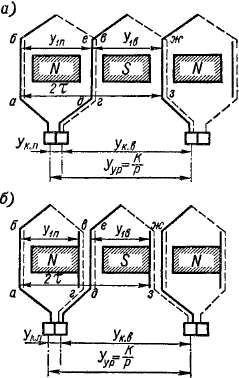Рис. 3-40. Два варианта выполнения комбинированной обмотки

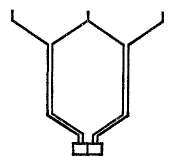Рис. 3-41. Форма катушки комбинированной обмотки

служить в качестве уравнителей первого рода для петлевой обмотки я одновременно уравнителями второго рода для петлевой (если она сложная) и волновой обмоток. Однако, как следует из рис. 3-40, а и б, коллекторные пластины, расположенные на расстоянии шага у_П, соединяются контуром абвгдежз секций петлевой и волновой обмоток, причем сумма э. д. с. этого контура при равенстве потоков полюсов равна нулю. Следовательно, сам этот контур играет роль уравнителя, и поэтому надобности в специальном уравнительном соединении нет.

Таким образом, комбинированная обмотка не нуждается в особых уравнителях, так как их роль выполняют элементы самой обмотки. Это является преимуществом обмоток такого типа в случаях, когда требуется наличие полного или большого числа уравнителей. Вместе с тем комбинированные обмотки сложны по конструктивному исполнению, охлаждение их лобовых частей хуже, а их естественные контуры для уравнительных токов имеют повышенную индуктивность, что ухудшает коммутацию (см. § 6-4). Поэтому применение этих обмоток ограничено.

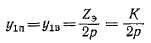
Секции комбинированной обмотки часто объединяют в катушки, форма катушки показана на рис. 3-41. Вследствие такой формы катушек комбинированную обмотку часто называют лягушачьей.

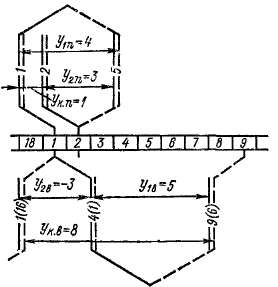
Рассмотрим пример комбинированной обмотки с данными: 2р-= 4, а_п = а_в — = 2, Z = Z_B ~ S = К = 18. Петлевая обмотка является простой, а волновая обмотка — двухходовой двукратно-замкнутой.

Шаги петлевой обмотки:

Условия (3-30) выполняются.

Элементы схемы обмотки изображены на рис. 3-42, причем, как и обычно, петлевая и волновая обмотки показаны по разным сторонам от коллектора.

Входящие в рассматриваемую комбинированную обмотку простая петлевая и сложная волновая обмотки имеют те же данные, что и обмотки, рассмотренные в § 3-3 и 3-6 (см. рис. 3-16, 3-17 и 3-19; рис. 3-37, 3-38 и 3-39), и поэтому полная схема ее представляет собой сочетание схем рис. 3-17 и 3-38. Векторные диаграммы на рис. 3-19 и 3-39 одинаковы, что свидетельствует о правильном выборе данных комбинированной обмотки и о ее хороших рабочих свойствах.

При сравнении схем рис. 3-38 и 3-42 следует иметь в виду, что на рис. 3-38 нумерация пазов выполнена так, как показано в нижней части рис. 3-42 в скобках.

Рис. 3-42. Элементы схемы комбинированной обмотки с 2р = 4, а_п = а_в = 2,

2 = z, = s = a:= is

§ 3-8. Выбор типа обмотки

Исходя из рациональных в практическом отношении размеров пазов, проводников обмотки, коллекторных пластин и щеток, а также из условий коммутации, ток параллельной ветви ограничивают значениями i_a = 300 -s- 350 а, а в отдельных случаях i_a — 400 -г-450 а. С другой стороны, в машинах малой мощности для получения заданного значения £/_н из-за малых значений Ф требуется большое число витков в ветви обмотки, что ограничивает сечение проводников и i_a. Поэтому в таких машинах применяется обмотка с минимальным числом ветвей, т. е. простая волновая обмотка, а в машинах больших мощностей — другие типы обмоток.

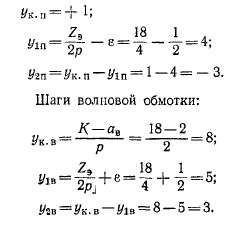
Соответственно этому при U_a = 220 в простая волновая обмотка используется до Р_н — 80 -*■ 100 кет, сложная волновая обмотка — при Р_н = 150 -ч- 300 кет, а простая петлевая обмотка — при Р_н = = 100 -н 500 кет и выше. Сложные петлевые обмотки применяются в машинах низкого напряжения (£/_н < 50 в) на большие токи и в крупных машинах нормального и повышенного напряжения (U_H > 110 в). При других напряжениях указанные мощности изменяются пропорционально £/„.

Комбинированные обмотки находят некоторое применение в машинах предельной мощности и при тяжелых режимах работы (быстро меняющиеся нагрузки и т. д.)- На выбор типа обмотки влияет также число полюсов, скорость вращения и т. д.

Значение и_П = I используется только в машинах низкого напряжения при больших токах. При U_H = 220 в и Р_н > 30 -*■ 50 кет число витков в секции всегда равно единице.

Содержание
Предыдущий § Следующий