Содержание
Предыдущий § Следующий

Глава четвертая ОСНОВНЫЕ ЭЛЕКТРОМАГНИТНЫЕ СООТНОШЕНИЯ

§ 4-1. Э. д. с. якоря и электромагнитный момент

Э. д. с. якоря. Обозначим буквой N число активных проводников обмотки и рассчитаем э. д. с. якоря Е_а в предположении, что у_х = = т и щетки установлены на геометрической нейтрали. Тогда э. д. с. всех NI2a проводников параллельной ветви складываются арифмв' тически и для вычисления Е_а можно просуммировать э. д. с. Nl2p проводников, расположенных под одним полюсом, и умножить результат на 2р/2а. Таким образом,

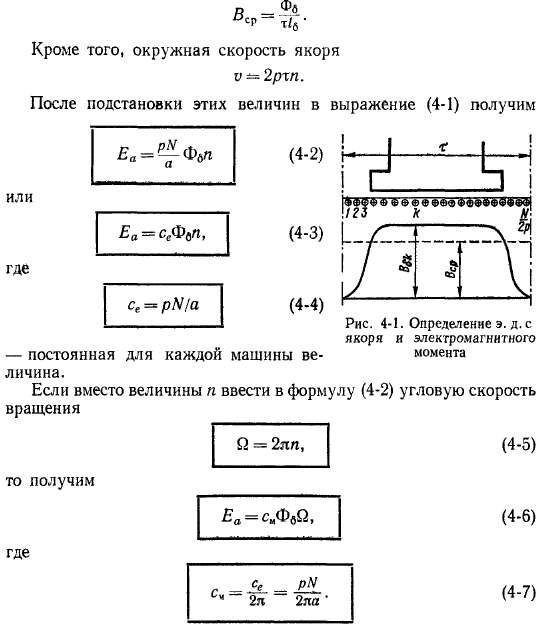
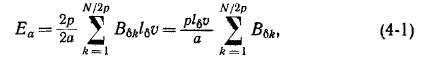где B$_k — значение индукции под k-м проводником на протяжении полюсного деления (рис. 4-1).

При достаточно большом N/2p можно положить (рис. 4-1)

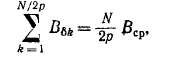
где В_ср — среднее значение магнитной индукции на протяжении полюсного деления, равное

Как следует из выражений (4-3) и (4-6), э. д. с. Е_а пропорциональна величине основного магнитного потока и скорости вращения и не зависит от формы кривой распределения индукции в воздушном зазоре.

При укороченном или удлиненном шаге обмотки в выражения (4-2), (4-3) и (4-6) вместо Ф_& нужно подставлять величину потока,

с которым сцепляется секция при симметричном ее расположении относительно полюса (рис. 4-2). При этом удлинение шага на некоторую величину А равноценно укорочению шага на такую же величину. При наличии скоса пазов нужно исходить из этого же принципа. Однако в обычных условиях, когда удлинение или укорочение шага, а также величина скоса пазов малы, влияние их мало и не учитывается»

Когда щетки сдвинуты с геометрической нейтрали, э. д. с. меньше. При этом в выражения (4-2), (4-3) и (4-6) нужно подставлять значение потока, с которым сцепляется секция в момент ее замыкания накоротко щетками. Если щетки сдвинуты с нейтрали на половину полюсного деления, то Е_а = 0.

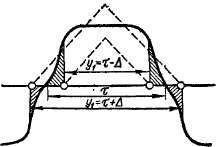Рис 4-2. Определение потока,

сцепляющегося с обмоткой при

неполном шаге

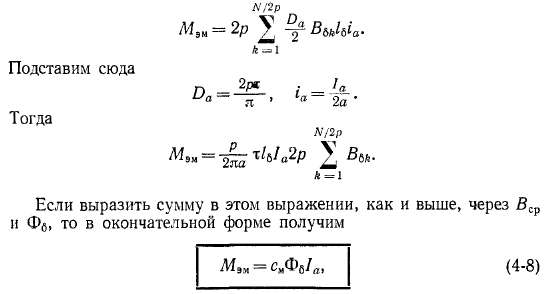
Электромагнитный момент и электромагнитная мощность. При тех же

предположениях, что и при определении Е_а, электромагнитный момент мятттины

причем постоянный для каждой данной машины коэффициент с„ определяется равенством (4-7).

Сделанные выше замечания о влиянии формы кривой поля, шага обмотки, скоса пазов и сдвига щеток с нейтрали действительны и для данного случая. Момент в системе СИ получается в ньютон-метрах (н-м). При необходимости выразить момент в килограмм-метрах (кгс -м) надо результат разделить на 9,81.

При выводе формул э. д. с. и момента предполагалось, что проводники обмотки расположены на гладкой поверхности якоря. В действительности проводники находятся в пазах, где магнитная индукция ослаблена. Однако полученные формулы справедливы и в этом случае, так как величины э. д. с. и момента определяются величиной потока, сцепляющегося с секциями обмотки. При расположении проводников в пазах механические усилия действуют главным образом не на проводники обмотки, а на зубцы якоря.

§ 4-2. Основные электромагнитные нагрузки и машинная постоянная

Электромагнитные нагрузки. Ниже в данной главе предполагается, что все рассматриваемые величины относятся к номинальному режиму, и для краткости это не указывается дополнительными индексами.

Важнейшими электромагнитными нагрузками электрической машины, определяющими степень использования материалов и размеры машины при заданной номинальной мощности, являются магнитная индукция в воздушном зазоре В_ь и линейная токовая нагрузка якоря А_а.

Последняя представляет собой общую величину тока обмотки якоря на единицу длины окружности якоря. Для машин постоянного тока

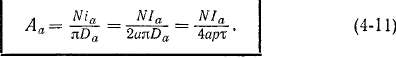В малых машинах вследствие малого диаметра якоря D_a геометрические соотношения зубцовой зоны менее благоприятны, так как

зубцовое деление у корня зубца значительно меньше, чем по внешней поверхности якоря. Поэтому во избежание сильного насыщения корня зубца в таких машинах приходится выбирать меньшие значения Be (см. § 2-5). Кроме того, у малых машин глубина паза меньше и вследствие малых размеров пазов и сечений проводников изоляция занимает относительно большую часть площади паза, чем у крупных машин. По этим причинам А_а в малых машинах также меньше, чем в крупных. В машинах постоянного тока при D_a = ■= 10 см и D_a = 300 см линейная нагрузка соответственно находится в пределах:

Л_й = (1,0-т-1,5) 10⁴ а/м =100 -г-150 а/см; А_а = (4,5 -ь 6,0) • 10⁴ а/м = 450 -ь 600 а/см.

Величина А_а, а также величина плотности тока якоря /„ ограничиваются в первую очередь условиями охлаждения.

Действительно, потери мощности в единице объема проводников обмотки якоря равны р]а, где р — удельное электрическое сопротивление проводника. С другой стороны, сечение проводников обмотки на единицу длины окружности якоря

S_ai = A_a/j_a.

Поэтому потери в обмотке якоря, приходящиеся на единицу поверхности якоря,

Р«1=15_й1рД = рЛ_а/а. (4-12)

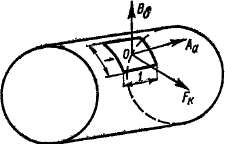Рис. 4-3 Определение средней ка-сательной силы

_{Чш больше PaV тем тр}уд_нее условия охлаждения обмотки якоря. В малых машинах, у которых А_а мало, )_а берут больше, а в крупных машинах — наоборот. Величину /„ также можно отнести к числу основных электромагнитных нагрузок. При D_a — Ю см в среднем /о та 10 а/мм?, а при D_a = 300 см обычно /„ = 4,0 -*- 5,5 а/мм². Средняя касательная сила. Величины В& и А_а определяют величину средней касательной силы /^ на единицу всей поверхности якоря (рис, 4-3):

Коэффициент полюсной дуги а_б учитывает здесь то обстоятельство, что индукция 5_в действует в пределах полюсного деления только на протяжении дуги а₆т (см. § 2-2), в результате чего среднее

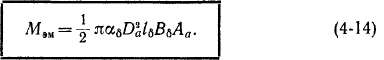электромагнитное усилие на единицу всей поверхности якоря соответственно уменьшается.

Если взять некоторые округленные величины из числа встречающихся на практике; а_б = 0,75, 5₈ = 0,8 тл, А_а = 5-Ю⁴ а/м, то F_K = 0,75 0,8-5-10⁴ = 3.10⁴ н/лг²»3-10³ кгс/м² = 0,3 кгс/см². Полученная величина характеризует реально достижимые электромагнитные усилия в электрических машинах.

Машинная постоянная Арнольда. Выражение для электромагнитного момента получим, если умножим F_K [см. формулу (4-13)1 на площадь поверхности якоря яЬ_й/§, а затем на плечо D_al2:

Умножив М_эм на Q = 2пп, получим зависимость Р_Эм от основных геометрических размеров, электромагнитных нагрузок и скорости вращения машины:

Эту же зависимость можно получить, если в выражение (4-10) подставить Е_а из формулы (4-2) и выразить Ф_е через В₆ и 1_а через А_а [см. соотношение (4-11)1.

Из выражения (4-15) определяется так называемая машинная постоянная Арнольда:

Величина С а пропорциональна объему якоря на единицу электромагнитного момента, так как DII& и P_BJn пропорциональны этим величинам. Согласна соотношению (4-16), величина С_А определяется электромагнитными нагрузками В₈, А_а и коэффициентом а₆.

На основании вь/ражения (4-16) можно сделать вывод, что чем выше электромагнитные нагрузки, тем меньше размеры и стоимость машины при заданной мощности и скорости вращения.

Ввиду высокого коэффициента полезного действия электрической машины величина Р_Ъ№ близка к Р_в и характеризует поэтому также номинальную мощность.

Из выражений (4-14) и (4-16) следует, что геометрические размеры машины определяют непосредственно не мощность ее, а электромагнитный момент и при данных размерах мощность

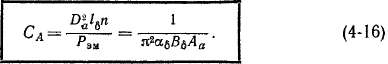
пропорциональна скорости вращения. Таким образом, при заданной мощности машины с большой скоростью вращения меньше по размерам, легче по весу и дешевле.

Если пользоваться, как это делается в практических руководствах, размерами см, об/мин и кет, то в формулу (4-15) надо вместо

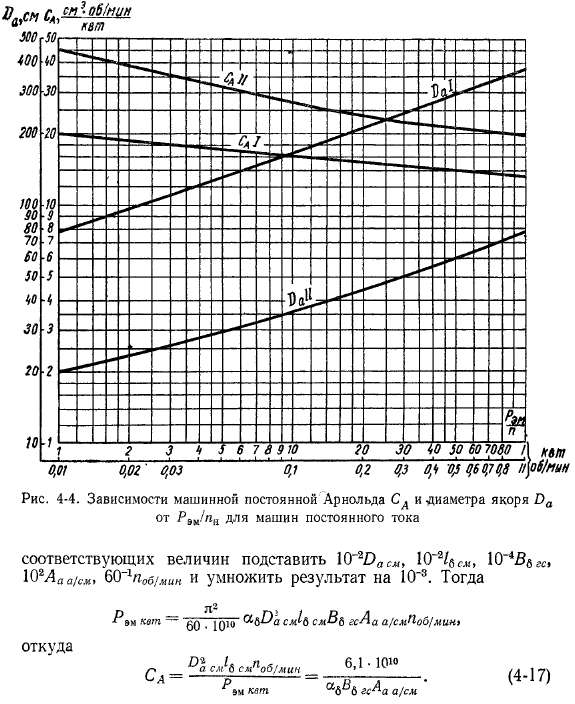
На рис. 4-4 показана зависимость С_А от Р,„_квт/п_об/_Мин- Она представляет собой падающую кривую, так как с увеличением геометрических размеров машины значения В₆ и А_а, как указано выше, увеличиваются.

Для машин переменного тока действительны зависимости, которые подобны рассмотренным и отличаются только числовыми коэффициентами [21, 22, 23, 83, 84, 85].

При проектировании машины по заданному значению Р_Эш1п из кривой рис. 4-4 можно найти С а, а затем

влияет на технико-экономические показатели машины. При увеличении К уменьшается относительная величина неактивных лобовых частей машины, однако ухудшаются условия охлаждения, и поэтому необходимо уменьшать значения В_& и А_а и т. д. В связи с этим существуют оптимальные значения К, при которых по весу, стоимости и технико-экономическим показателям получается наилучший вариант машины. Оптимальные значения А. устанавливаются в результате технико-экономических расчетов и исследования опытных данных [40, 41].

Если оптимальное значение к известно, то по соотношениям (4-18) и (4-19) можно определить по отдельности 4 и D_a. На рис.4-4 приведена кривая D_a, соответствующая оптимальным значениям X. По известным Са и D_a, согласно выражению (4-18), можно найти также /g.

Аналогичным образом определяются также основные размеры при проектировании машин переменного тока [21, 22, 23, 83, 84, 85].

§ 4-3. Влияние геометрических размеров

на технико-экономические показатели машины

Рассмотрим ряд подобных в геометрическом отношении машин. Все геометрические размеры (длина и диаметр якоря, полюсное деление, ширина и высота пазов и т. д.) любой машины этого ряда отличаются от размеров другой машины этого же ряда в одинаковое число раз. Предположим, что у всех машин данного ряда плотность тока и магнитные индукции в соответствующих частях машин, а также скорость вращения одинаковы. В таком случае можно рассматривать зависимость мощности, потерь и других величин от какого-либо характерного для машины геометрического размера /, например, / = D_a или / = /_е.

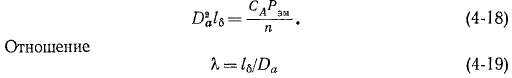
98                                                             Машины постоянного тока [Разд. I

В геометрически подобных машинах общая площадь пазов изменяется прямо- пропорционально I² и при j_a — const общий объем тока в пазах также изменяется прямо пропорционально Р. Так как диаметр якоря изменяется прямо пропорционально I, то при этом А_а ~ I. Поэтому при указанных условиях, согласно выражению (4-15),

Р ~ /⁴.                                       (4-20)

К этому выводу можно прийти и иначе. Действительно, при N = const сечение проводника, а следовательно, и ток якоря 1_а изменяются пропорционально /². Площадь поверхности якоря на один полюс, а значит, поток Фв и э. д. с. Е_а также изменяются пропорционально /², Следовательно, мощность

С другой стороны, объем машины V, ее вес G и стоимость С прямо пропорциональны I^s:

V~G~C~t³,                        (4-21)

и, следовательно,

G с 1                                    ,. _ооч

-рг — -р ~ т ■                                 (4-22)

Это значит, что вес машины и ее стоимость на единицу мощности уменьшаются с увеличением геометрических размеров обратно пропорционально I.

При В = const, / = const и / = const электрические и магнитные потери мощности в отдельных частях машины на единицу объема также постоянны. Следовательно, эти потери растут прямо пропорционально I³. То же приблизительно верно и для механических потерь. Поэтому суммарные потери

Таким образом, потери на единицу мощности при увеличении / и Р уменьшаются, а к. п. д. машины увеличивается.

Величина поверхностей охлаждения S_0O, с которых отводятся выделяющиеся в виде тепла потери Р₂> растет прямо пропорционально Р, и поэтому

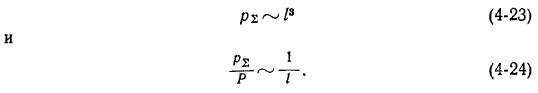
Следовательно, величина потерь на единицу поверхностей охлаждения растет прямо пропорционально /, и поэтому условия охлаждения в крупных машинах ухудшаются.

Это вызывает необходимость совершенствования способов охлаждения электрических машин при увеличении их размеров и мощности,

Полученные зависимости не вполне точны, так как произведение В_ьА_а в действительности увеличивается медленее, чем I (см. §4-2). Однако эти зависимости вполне четко выявляют общие закономерности и тенденции и притом в одинаковой степени как для машин постоянного, так и для машин переменного тока.

Из полученных зависимостей следует, что относительный расход материалов и относительная стоимость у крупных машин всегда меньше, а к. п. д. выше, чем у малых машин. Аналогичным образом нетрудно установить, что при сохранении неизменными геометрических размеров и электромагнитных нагрузок вес, стоимость и потери на единицу мощности с увеличением скорости вращения уменьшаются.

Поэтому экономически целесообразно строить и применять, где это возможно, крупные и быстроходные электрические машины.

Содержание
Предыдущий § Следующий