Содержание
Предыдущий § Следующий

Глава тридцать восьмая НЕСИММЕТРИЧНЫЕ РЕЖИМЫ РАБОТЫ СИНХРОННЫХ ГЕНЕРАТОРОВ

§ 38-1. Действие симметричных составляющих токов в синхронной машине и параметры прямой, обратной и нулевой последовательности

Предварительные замечания. На практике встречаются случаи, когда мощные однофазные потребители нарушают симметричную нагрузку фаз синхронных генераторов (тяговые подстанции железных дорог, электрифицируемых на переменном токе, и т. д.). Еще более часто, хотя и кратковременно, несимметричная нагрузка фаз генераторов возникает при несимметричных коротких замыканиях в электрических сетях: при однофазном коротком замыкании — между линейным и нулевым проводами, при двухфазном коротком

замыкании — между дв^мя линейными проводами и при двухфазном коротком замыкании на нейтраль — между двумя линейными и нулевым проводами. Роль нулевого провода в сетях высокого налряже-ния играет земля, так как нулевые точки в таких сетях обычно заземляются.

Хотя несимметричные короткие замыкания существуют кратковременно, так как поврежденные участки сетей отключаются релейной защитой, они оказывают сильное влияние на работу генераторов и сети в целом. При внезапных несимметричных коротких замыканиях возникают также переходные процессы, однако ниже для выявления главных особенностей явлений рассматриваются прежде всего установившиеся несимметричные режимы работы.

Общим методом исследования несимметричных режимов является метод симметричных составляющих, при котором несимметричная система токов раскладывается на симметричные составляющие и действие последних учитывается по отдельности. В данном параграфе рассмотрим действие токов равных последовательностей в трехфазной синхронной машине.

Токи и сопротивления прямой последовательности. При симметричной нагрузке синхронного генератора существуют только токи прямой последовательности. Поэтому изложенное в гл. 32 и 33 относится к работе синхронных машин с токами прямой последовательности и введенные там синхронные сопротивления x_d и x_q являются сопротивлениями синхронной машины для токов прямой последовательности.

Наиболее существенной особенностью нормального режима работы синхронной машины с токами прямой последовательности является то, что ротор машины вращается синхронно с полем токов прямой последовательности или полем реакции якоря и поэтому это поле не индуктирует в цепях индуктора никаких токов. По этой причине сопротивления x_d и x_q велики.

Пользуясь терминологией теории асинхронных мащин, можно сказать, что скольжение s ротора синхронной машины относительно магнитного поля токов прямой последовательности статора (якоря) равно нулю. Поэтому сопротивления х_а и x_q идентичны с индуктивным сопротивлением асинхронной машины при идеальном холостом ходе (s = s_x = 0).

Составляющими этого сопротивления являются индуктивное сопротивление рассеяния х_аа и индуктивное сопротивление от основной гармоники поля в воздушном зазоре (для синхронной машины

Токи и сопротивления обратной последовательности. Представим себе, что обмотка якоря (статор) синхронной машины питается напряжением обратной последовательности U₂.

Возникающие при этом токи обратной последовательности создают магнитное поле обратной последовательности, которое вращается по отношению к статору с синхронной скоростью в обратном направлении, а по отношению к ротору, вращающемуся с синхронной скоростью в прямом направлении, — с удвоенной синхронной скоростью. Поэтому относительно этого поля скольжение ротора s₂ = 2 и в обмотках возбуждения, успокоительной и в массивных частях ротора индуктируются вторичные токи двойной частоты, которые вызывают соответствующие потери и нагрев ротора.

Ввиду сказанного для рассматриваемого случая действительно все изложенное в § 36-1 при s = 2.

Схемами замещения для токов обратной последовательности являются схемы рис. 36-2 при s = 2. Обозначим сопротивления этих схем при s = 2 буквами Z_d2 и Z_g2.

При Z_d2 ф Z₉₂ токи статора содержат составляющую основной частоты и, согласно выражению (36-4), токи тройной частоты, влиянием которых можно пренебречь. Ток основной частоты представляет собой ток обратной последовательности /₂ и определяется первым равенством (36-3) при s = 2:

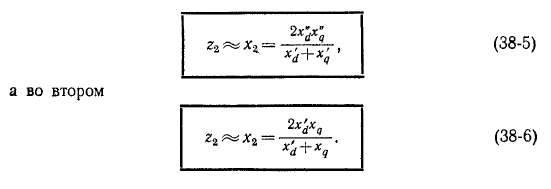
Поэтому в первом случае в соответствии с равенством (38-2)

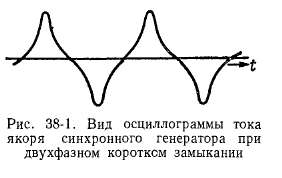
Сопротивление Z₂ по формуле (38-2) соответствует случаю, когда напряжения статора синусоидальны, а токи несинусоидальны Если последовательно с обмоткой статора включены значительные индуктивные сопротивления (например, сопротивления трансформаторов и линий передачи), то токи обратной последовательности синусоидальны, а напряжения обмотки статора несинусоидальны. В этом случае, как можно показать,

При этом высшие гармоники тока и напряжения отсутствуют.

Вследствие экранирующего влияния вторичных токов сопротивление *₂ значительно меньше х_а и x_q (см. табл. 32-1). Сопротивления 2₂, х₂ ^и h можно определить по измеренным значениям U₂, /₂ и потребляемой активной мощности Р₂, если приключить синхронную

машину к источнику с симметричной системой напряжений и вращать ротор против поля с синхронной скоростью. Во избежание перегрева ротора необходимо, чтобы /₂ = (0,2 -г- 0,25) /_н. Если машина не имеет успокоительных обмоток и контуров, то для получения более правильных результатов надо из осциллограмм выделить основные гармоники тока и напряжения.

Токи и сопротивления нулевой последовательности.

Токи нулевой последовательности обмотки статора /₀ создают в воздушном зазоре только пульсирующие поля гармоник v = = 3, 9, 15..., а основная гармоника поля будет отсутствовать (см. § 22-2). Эти гармоники поля индуктируют в обмотках возбуждения и успокоительной токи, величины которых относительно невелики.

Сопротивление нулевой последовательности

Индуктивное сопротивление нулевой последовательности х₀ ввиду отсутствия поля основной гармоники относительно невелико (см. табл. 32-1) и определяется полями пазового и лобового рассеяния обмотки статора и указанными выше гармониками поля в зазоре. Активное сопротивление нулевой последовательности г₀ в результате потерь, вызываемых гармониками поля в роторе, несколько больше активного сопротивления обмотки статора г_а, но разность г₀ — г_а невелика и г₀ !=& г_а. Вращающий момент, создаваемый токами /₀, практически равен нулю.

Сопротивления г₀, х₀ и, г₀ можно определить опытным путем, если при вращении машины с синхронной скоростью питать после* довательно включенные фазы обмотки статора током /₀. Указанные сопротивления при этом определяются точно так же, как и у трансформатора (см. § 16-1).

§ 38-2., Работа синхронных генераторов при несимметричной нагрузке

Обмотка статора синхронных генераторов обычно включается в звезду, причем нулевая точка в малых машинах изолирована, а в крупных машинах с целью выполнения релейной защиты от замыканий на землю заземляется через большое сопротивление. Поэтому токи нулевой последовательности либо отсутствуют, либо весьма невелики.

В силу этого при несимметричной нагрузке синхронных генераторов, кроме токоп прямой последовательности, практически существуют только токи обратной последовательности.

I Последние вызывают в машине ряд нежелательных явлений и делают режим работы машины тяжелым.

Потери энергии и нагрев ротора.

Токи двойной частоты, индуктируемые в роторе магнитным полем статора обратной последовательности, вызывают в роторе излишние потери и его нагрев, а также уменьшение к. п. д. машины.

Токи, индуктируемые -обратным полем в успокоительных обмотках явнополюсных машин и в массивном роторе турбогенераторов, могут быть весьма значительными, а активные сопротивления этим токам под влиянием поверхностного эффекта будут большими.

Поэтому при значительной несимметрии нагрузки возникает чрезмерный и опасный нагрев успокоительных обмоток и массивных роторов.

Высокая температура тела ротора турбогенератора вызывает опасные деформации ротора и вероятность повреждения изоляции обмотки возбуждения. Нагрев успокоительной обмотки явнополюс-ной машины мало влияет на температуру обмотки возбуждения ввиду удаленности этих обмоток друг от друга и лучших условий охлаждения обмотки возбуждения явнополюсных машин.

Токи, индуктируемые обратным полем в обмотке возбуждения, меньше из-за большего сопротивления рассеяния этой обмотки. Поэтому в явнополюсных машинах дополнительный нагрев обмотки возбуждения при несимметричной нагрузке невелик.

Вибрация.

В результате взаимодействия потока возбуждения и потока обратной последовательности статора, а также поля прямой последовательности статора и поля токов двойной частоты ротора при несимметричной нагрузке на ротор и статор действуют знакопеременные вращающие моменты и тангенциальные силы, пульсирующие с частотой 2/_х.

Кроме того, вследствие этих же причин возникают пульсирующие радиальные силы притяжения и отталкивания между полюсами полей статора и ротора, стремящиеся деформировать статор и ротор. Эти силы вызывают вибрацию частей машины, шум и ослабление запрессовки сердечника статора. Пульсирующие силы двойной частоты ввиду усталостных явлений могут также вредно отразиться на прочности сварных соединений, в особенности при наличии дефектов сварки. Все указанные факторы, естественно, тем сильнее, чем больше несимметрия нагрузки.

Искажение симметрии напряжений. Токи обратной последовательности вызывают в фазах обмотки статора падения напряжения

Z₂/₂, векторы которых ориентированы относительно напряжений прямой последовательности в разных фазах по-разному.

В результате этого симметрия напряжений генератора искажается и напряжения более загруженных фаз будут меньше. Это ухудшает условия работы приемников, в особенности асинхронных и синхронных двигателей.

В машинах с успокоительными обмотками и массивными роторами или полюсами Z₂ меньше, вследствие чего и искажение симметрии напряжений у них меньше. Физически это объясняется тем, что в таких машинах поток обратной последовательности статора в значительной степени заглушается токами, индуктируемыми в роторе, и поэтому этот поток индуктирует в фазах обмотки статора меньшие э. д. с.

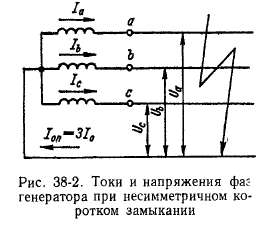
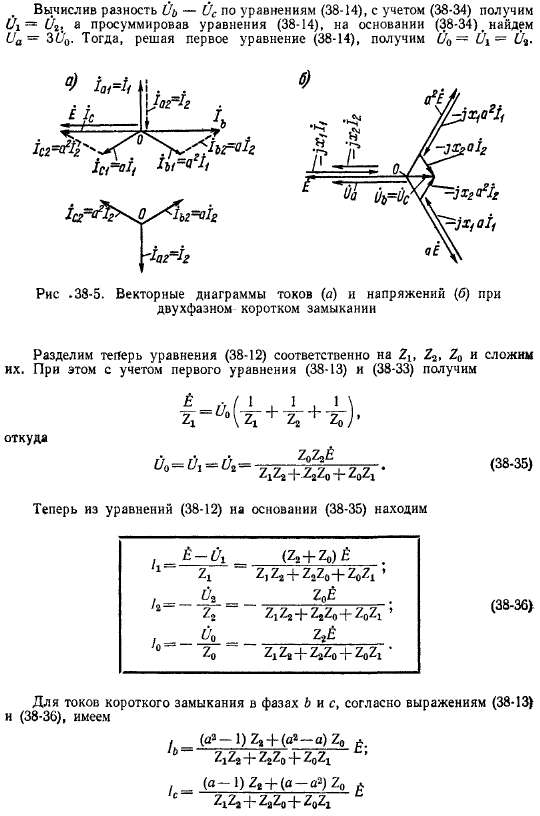
Высшие гармоники токов и напряжений. Как было установлено выше, ввиду неравенства сопротивлений по продольной (Z_di) и поперечной (Z_?2) осям возникает третья гармоника тока с частотой 3/х- В особенности сильное искажение формы кривой ток,а происходит при несимметричных коротких замыканиях, так как при этом сглаживающее влияние внешних индуктивных сопротивлений исчезает или ослабляется. В качестве примера на рис. 38-1 изображена форма кривой тока при двухфазном коротком замыкании.

Высшие гармоники тока могут вызвать опасные резонансные явления, если в цепях обмоток статора имеются емкости (например, емкость длинных линий передачи и пр.).

В результате резонанса напряжений на зажимах обмотки статора возникают напряжения повышенных частот, которые могут превысить номинальные напряжения во много раз и повредить изоляцию машины. Это является одной из причин того, что мощные гидрогенераторы, работающие на длинные линии передачи, обычно снабжаются успокоительными обмотками. При наличии успокоительных обмоток Z_rfa m Z_?2 и x"d ~ x"_q, вследствие чего в этом случае токи остаются синусоидальными и опасность указанных перенапряжений исчезает.

Допустимая несимметрия нагрузки ограничивается прежде всего необходимостью предотвращения опасного нагрева ротора, а также вибрации машины.

Согласно ГОСТ 183—66, допускается длительная работа турбо-и гидрогенераторов с несимметричной нагрузкой, если токи фаз не превышают номинальных значений и разность токов в фазах не превышает 10% номинального тока фазы.

§ 38-3. Несимметричные короткие замыкания

Основные уравнения. Рассмотрим установившиеся несимметричные короткие замыкания на зажимах генератора с соединением обмоток в звезду в предположении, что они происходят при работе на холостом ходу, и определим величины токов коротких замыканий. Для этого составим прежде всего уравнения, связывающие между собой токи (/], /₂, /₀), * сопротивления (Z\, 2₂, Z_o) и напряжения (U_lt U₂, U_o) разных последовательностей, причем Ui, U₂ и U_o являются" составляющими напряжений фаз U_a, lib, U_c в месте короткого замыкания (рис. 38-2).

Ток возбуждения индуктирует только э. д. с. прямой последовательности ¹ Ei = Е, и поэтому £₂ = Е_а = 0. Так как цепи фаз вплоть до места короткого замыкания симметричны, то уравнения напряжений для разных последовательностей независимы друг от друга и для фазы а имеют вид

Кром« того, существуют следующие зависимости между токами и напряжениями фаз и их симметричными составляющими:

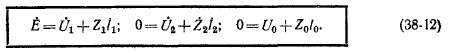
бенностей каждого вида короткого замыкания, необходимо составить три дополнительных уравнения.

Сначала целесообразно определить симметричные составляющие токов и напряжений, а затем по уравнениям (38-13) и (38-14) найти фазные величины.

Из уравнений (38-12) можно определить симметричные составляющие напряжений:

Если подставить эти значения U_lt (]_г, й_а в уравнения (38-14), то последние приобретают вид

Согласно выражениям (38-16), напряжения фаз равны э. д. с. фаз Ё, а²Ё и аЁ минус падения напряжения от токов разных последовательностей в сопротивлениях соответствующих последовательностей.

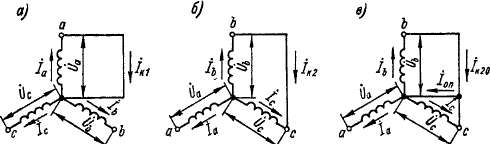Рис. 38-3. Схемы однофазного (а), двухфазного (б) и двухфазного на нейтраль (в) короткого замыкания синхронного генератора

Уравнения (38-12) — (38-16) действительны не только для несимметричных коротких замыканий, но и для общего случая несимметричной нагрузки синхронного генератора. Однако ниже он-и будут использованы для исследования несимметричных коротких замыканий.

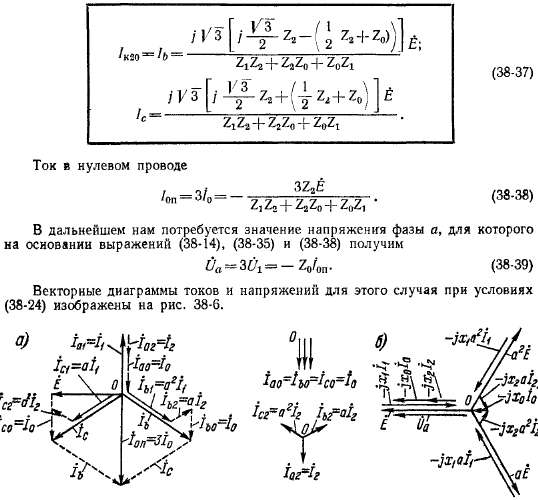
Однофазные короткие замыкания. В этом случае, согласно схеме рис. 38-3, а,

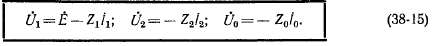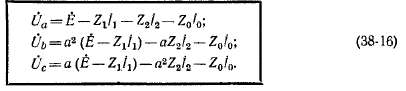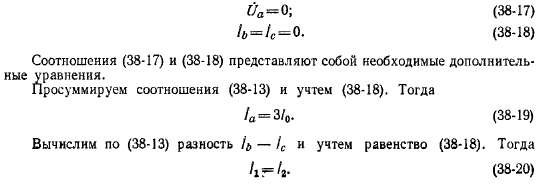
или после подстановки значений а и о²

Рис. 38-6. Векторные диаграммы токов (а) и напр-яжений (б) при двухфазном коротком замыкании на нейтраль

Комплексные схемы замещения. Полученные результаты позволяют составить для различных видов коротких замыканий весьма простые комплексные схемы замещения, которые включают в себя сопротивления различных последовательностей и определяют соотношения между токами и напряжениями различных последовательностей.

На рис. 38-7, а на основании равенства (38-22) представлена такая схема для однофазного короткого замыкания. Генератор изображен в качестве источника э. д. с. Е, последовательно с ним соединено сопротивление прямой последовательности Z%, а между точками М и N , условно изображающими место короткого замыкания, включены последовательно Z₂ и Z_o. Ниже мы увидим, что такая структура схемы сохранится и для других видов коротких замыканий, но в месте короткого замыкания, между точками М и N, будут действовать другие величины сопротивлений.

Очевидно,что схема рис. 38-7, а вполне соответствует равенству (38-22). На этой схеме, кроме того, на основании уравнений (38-15) показано, между какими точками схемы действуют напряжения разных последовательностей. Как в данном,

так и в других случаях напряжение Ui действует между условными точками короткого замыкания М и Л', a U₂ и U_o равны падениям напряжения соответственно в сопротивлениях Z₃ и Z_o.

На рис. 38-7, б на основании равенства (38-28) представлена комплексная схема замещения для двухфазного короткого замыкания, а указанные там напряжения также определяются уравнениями (38-15). На рис. 38-7, в изображена схема для двухфазного короткого замыкания на нейтраль, соответствующая равенствам (38-36), а также (38-15) и (38-35). Наконец, на рис 38-7, г, согласно изложенному в § 33-2, изображена схема для трехфазного короткого замыкания. В этом случае

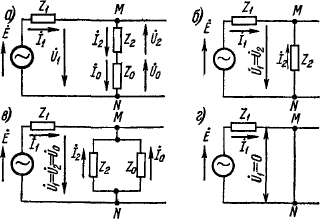Рис. 38-7. Комплексные схемы замещения для однофазного (а), двухфазного (б), двухфазного на нейтраль (в) и трехфазного (г) короткого замыкания синхронного генератора

Установив вид комплексных схем замещения, можно не решать уравнения, как это было сделано выше, а выписать выражения _ для 1_и h> h ^и U_lt U₂, й₀ непосредственно на основе схем замещения. Если на схеме сопротивление какой-либо последовательности отсутствует, то соответствующие составляющие тока и напряжения равны нулю Можно показать, что схемы рис. 38-7 действительны не только для рассмотренных простейших коротких замыканий, но и для несимметричных коротких замыканий в сложной сети, причем в последнем случае под Z₁₍ Z₂ и Z_o нужно понимать сопротивления всей сети для токов соответствующих последовательностей.

Сравнение различных видов коротких замыканий. Если сопротивление нулевого провода равно нулю и короткие замыкания происходят на зажимах машины, то г₁ > г₂ > г₀ или при пренебрежении активными сопротивлениями Zj = х^ > г₂ = = х_% > г₀ = х₀ (см. тйбл. 32-1). В этом случае на основании равенств (38-23), (38-29), (38-37) и (38-40) можно установить, что при одинаковых Е будет ^ki > ^кг > ^кго > ^кз- Физически это можно объяснить тем, что при однофазном коротком замыкании размагничивающую реакцию якоря создает только ток одной фазы и поэтому в данном случае величина тока короткого замыкания получается наибольшей, а по мере увеличения числа короткозамк-нутых фаз их токи уменьшаются. С другой стороны, как видно из схем рис. 38-7, для токов прямой последовательности действительны обратные соотношения: наибольшая величина /_х соответствует трехфазному, а наименьшая — однофазному короткому замыканию. В соответствии со сказанным на рис. 38-8 изображены характеристики коротких замыканий.

При вычислении величин токов коротких замыканий всегда можно пользоваться соотношениями (38-24). Отметим, что, кроме рассмотренных выше токов

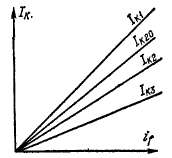Рис. 38-8. Характеристики несимметричных и симметричных коротких замыканий синхронного генератора

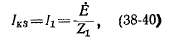
основной частоты, при несимметричном роторе (отсутствие успокоительных обмоток и контуров) возникают также высшие гармоники токов.

Определение сопротивлений обратной последовательности. Данные опыта двухфазного короткого замыкания используются для определения г₂, х₂ и г₂. На рис. 38-9 показаны схемы двухфазного короткого замыкания с включением приборов для измерения необходимых величин, обозначения которых указаны рядом с условными изображениями приборов.

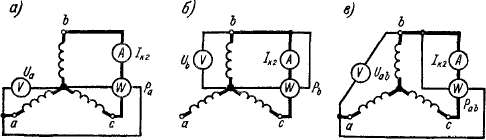Рис. 38-9 Схемы для определения сопротивления обратной последовательности по данным опыта двухфазного короткого замыкания

Для модуля полного сопротивления по показаниям измерительных приборов на основании равенств (38-32) для схем рис. 38-9, а, б я в соответственно

ПОЛУЧИМ

ГОСТ 10169—62 на испытание синхронных машин рекомендует использовать схему рис. 38-9, в и последние из соотношений (38-41) и (38-42). Следует иметь в виду, что при отсутствии успокоительных обмоток и контуров получаемые

результаты из-за наличия высших гармоник будут неточными. Для учета влияния этих гармоник можно ввести поправки, которые здесь не рассматриваются. Определение сопротивлений нулевой последовательности. Для этой цели используются данные опыта двухфазного короткого замыкания на нейтраль, выполняемого согласно схеме рис. 38-10. В соответствии с равенством (38-39)

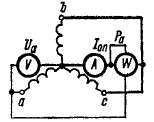Рис. 38-10. Схема для определения сопротивлений нулевой последовательности по данным опыта двухфазного короткого замыкания на нейтраль

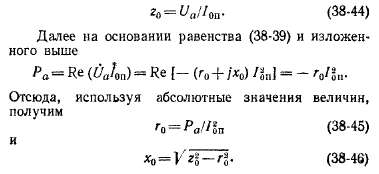Внезапные несимметричные короткие замыкания.

Как и при внезапном трехфазном коротком замыкании, в этом случае также во всех обмотках возникают апериодические и периодические токи. При внезапных несимметричных коротких замыканиях периодические токи якорд будут содержать составляющие тех же последовательностей /_х, 7₂, /₀, как и при установившихся коротких замыканиях. Как вытекает из более подробного рассмотрения этого вопроса, амплитуды начальных значений периодических токов якоря можно вычислить по равенствам (38-23), (38-29) и (38-37), если подставить в них вместо Z\, 2_г и Z_o соответственно jxd (или jx'd),jx₂ и]х₀ и умножить результаты на Yi, а амплитуды установившихся значений периодических токов вычисляются так же, но вместо ]x"_d (или jxjfi надо подставить /%• Разность начальных и конечных значений периодических токов затухает с постоянными времени T'_d, Т_а, как и при трехфазном коротком замыкании, но при несимметричных коротких замыканиях эти постоянные имеют другие значения. Начальные значения апериодических токов якоря равны по величине и обратны по знаку периодическим токам и также затухают с соответствующими постоянными времени.

Более подробно внезапные несимметричные короткие замыкания рассматриваются в специальных руководствах [68, 69, 72, 73, 75, 76, 79J.

Содержание
Предыдущий § Следующий