Содержание
Предыдущий § Следующий

Глава тридцать девятая КОЛЕБАНИЯ И ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ СИНХРОННЫХ МАШИН

§ 39-1. Физическая сущность колебаний синхронных машин

При колебаниях или качаниях синхронной машины ее ротор вращается неравномерно и скорость его колеблется с некоторой частотой около среднего значения.

Наибольший практический интерес представляет случай, когда машина работает параллельно с мощной сетью, частоту /_х тока которой можно считать постоянной. В этом случае колебания угловой скорости ротора Q, происходят около синхронной угловой скорости

Одновременно с колебаниями Q происходят также колебания угла нагрузки S.

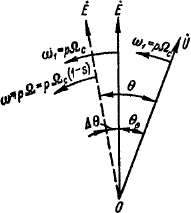Рис. •39-1. Векторы э. д. с. и напряжения синхронного генератора при колебаниях

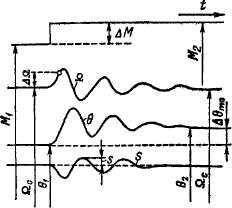Рис. 39-2. Колебания угловой скорости Й, угла нагрузки в и скольжения s синхронного генератора при внезапном изменении вращающего момента на валу М

Действительно, при_# п > Q_c ротор забегает вперед и угол 8 между векторами Ё и 0 при работе в режиме генератора увеличивается (рис. 39-1), а при U <Z Q_c уменьшается.

Колебания угла е в свою очередь неразрывно связаны, как следует из векторных диаграмм, с колебаниями величин мощности Р и тока якоря /.

Поэтому внешне колебания синхронной машины проявляются в колебаниях стрелок ваттметров и амперметров. Чем больше амплитуда колебаний. Q и е, тем больше также колебания Р и /. Если мощность сети мала, то возникают также колебания величины напряжения U.

При й =fc Q_c ротор вращается с некоторым скольжением s относительно магнитного поля статора, и поэтому при колебаниях синхронной машины колеблется также величина s. На рис. 39-2 представлены кривые затухающих колебаний Q, 6 и s. Индексы 1

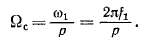
относятся к исходному режиму, до начала колебаний, а индексы 2 — к последующему режиму, после затухания колебаний.

В ряде случаев возникают весьма сильные колебания синхронных машин, которые серьезным образом нарушают их нормальную работу, а также работу энергосистемы в целом.

При колебаниях в синхронных машинах происходят сложные переходные процессы, которые ниже рассматриваются лишь в основных чертах и преимущественно с физической точки зрения.

Колебания синхронных машин бывают вынужденные и свободные.

Вынужденные колебания синхронной машины возникают в случаях, когда механический момент на валу непостоянен и содержит пульсирующие составляющие.

Чаще всего это бывает при соединении синхронных машин с поршневыми машинами (например, дизельный первичный двигатель у генератора и поршневой компрессор у двигателя).

Вынужденные колебания становятся особенно сильными, нежелательными и опасными, когда их частота /_в близка к частоте собственных или свободных колебаний /₀ и поэтому возникают резонансные явления, а также когда в общую сеть включено несколько синхронных машин, имеющих вынужденные колебания с одинаковыми или кратными частотами. Например, иногда возникают затруднения при параллельной работе так называемых синхронных дизель-генераторов, первичными двигателями которых являются дизели.

Для уменьшения вынужденных колебаний дизель-генераторы, а часто также двигатели поршневых компрессоров снабжаются маховиками. Маховики иногда присоединяются непосредственно к роторному колесу синхронной машины или ротор машины выполняется с повышенным маховым моментом (больший диаметр и вес). Дизель-генераторы имеют для уменьшения колебаний также успокоительные обмотки (о роли последних см. ниже).

Свободные колебания присущи самой природе синхронной машины, так как она при параллельной работе с сетью или другими синхронными машинами представляет собой колебательную систему.

Такие колебания возникают при любых внезапных или резких нарушениях или изменениях режима работы синхронной машины (наброс или сброс нагрузки, падение напряжения на зажимах, изменение тока возбуждения и пр.). Изображенные На рис. 39-2 колебания возникают; например, при внезапном увеличении вращающего момента первичного двигателя, как это показано в верхней части рисунка. В этом случае угол нагрузки генератора возрастает

от 9i до 6₂> и этот переход совершается путем колебаний с начальной амплитудой колебаний угла нагрузки, равной |Лб_т0 = б₂ —■ Ь\.

Свободные колебания присущи многим физическим объектам, причем их природа и характер у разнородных объектов во многом одинаковы и колебания этих объектов описываются аналогичными дифференциальными уравнениями.

Колебания ротора синхронной машины являются механическими. Такие колебания возникают в механических системах, в которых действуют упругие и инерционные силы, при всяких возмущениях, выводящих эту систему из положения равновесия. Упругие силы, стремящиеся вернуть колеблющуюся систему в положение равновесия, зависят от величины отклонения системы от положения равновесия и в простейшем случае пропорциональны этому отклонению. В положении равновесия эти силы равны нулю. Силы инерции стремятся препятствовать изменению скорости движения системы и пропорциональны ускорениям механических масс. Когда под воздействием упругой силы система подходит к положению равновесия, то вследствие инерции она переходит через это положение. При этом направление упругой силы изменяется на обратное, система вновь начинает приближаться к положению равновесия, но под влиянием инерции переходит его и т. д. Во время колебаний упругие и инерционные силы беспрерывно изменяются по величине и по знаку. В результате этого во время колебаний происходит беспрерывное превращение потенциальной энергии, связанной с упругими силами, в кинетическую, связанную с инерционными силами, и обратно. При колебаниях обычно действует также успокаивающая, или демпфирующая сила, которая вызывает затухание колебаний.

Затухание происходит тем сильнее, чем больше эта сила. Если она равна нулю, то колебания являются незатухающими, т. е. происходят с постоянной амплитудой.

Простейшим примером механической колебательной системы является спиральная пружина с подвешенным к ней грузом. При нарушении равновесия, например, путем внезапного увеличения или уменьшения веса груза система приходит в колебания, причем амплитуда колебаний равна разности положений груза в конечном и начальном положениях равновесия. Упругая сила в данном случае — это сила упругой деформации пружины, инерционная сила — сила инерции колеблющегося груза и успокаивающая сила — сила трения колеблющегося груза о воздух. Частота колебаний тем больше, чем больше жесткость пружины и чем меньше масса груза.

|При свободных колебаниях синхронной машины действуют совершенно аналогичные силы или, вернее, вращающие моменты,

поскольку в данном случае происходят колебания вращающегося тела — ротора синхронной машины. Упругим силам в данном случае соответствует электромагнитный момент, действующий на ротор и зависящий от угла нагрузки 6 (см. § 35-3). Деформация магнитного поля в зазоре при изменении угла нагрузки (см. рис. 35-6) аналогична деформации пружины и вызывает изменение электромагнитного момента. В этом отношении линии магнитной индукции уподобляются упругим нитям, играющим роль пружины. Инерционным-еилам соответствует инерционный, или динамический, вращающий момент ротора, возникающий при наличии положительного или отрицательного углового ускорения ротора.

Частота собственных колебаний синхронных машин /₀ обычно составляет 0,5—2,0гц.

Успокоительный момент синхронной машины, вызванный трением ее ротора о воздух и в подшипниках, весьма невелик, и им можно пренебречь.

Успокоение колебаний синхронной машины происходит в основном за счет момента, возникающего в результате того, что при

колебаниях ротор попеременно движется то быстрее, то медленнее магнитного поля статора и поэтому в обмотках возбуждения и успокоительной индуктируются токи. Этот успокоительный момент по своей природе вполне идентичен с асинхронным моментом синхронной машины (См. § 36-1), стремится восстановить синхронную скорость вращения и заглушить колебания, так как при п > Q_c и s < 0 он является тормозящим, а при п < Q_c и s>0 действует в сторону вращения ротора и является ускоряющим.

Обмотка возбуждения создает относительно слабый успокоительный момент, в особенности, когда угол 9 мал (область нормальных нагрузок) или близок к нулю (холостой ход). Это объясняется тем, что при 8=0 поток реакции якоря является чисто продольным-и небольшие смещения ротора относительно этого потока вызывают лишь небольшие изменения потокосцепления ротора, вследствие чего и токи, индуктируемые в этой обмотке, невелики.

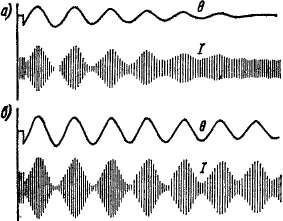
Рис. 39-3 Свободные колебания синхронной машины при наличии (я) и отсутствии (б) успокоительной обмотки

Эффективным средством успокоения колебаний является Применение полной успокоительной обмотки (рис. 39-3), создающей большой успокоительный момент. Основное назначение этой обмотки как раз и заключается в успокоении свободных колебаний, откуда происходит и ее название.

§ 39-2. Колебания синхронной машины

Рассмотрим сначала случай, когда амплитуда колебаний угла нагрузки мала. При этом дифференциальное уравнение движения ротора является линейным и имеет простое решение, позволяющее выяснить существенные особенности колебательного процесса синхронной машины. Для изучения этого вопроса составим уравнение вращающих моментов синхронной машины при" ее колебаниях и для определенности будем иметь в виду режим генератора, хотя получаемые результаты будут действительны и для двигателя.

Вращающие моменты, действующие при колебаниях. В соответствии с соотношением (35-4) электромагнитный момент выражается равенством

Пусть колебания совершаются около значения угла б = 8₀. соответствующего состоянию равновесия, когда электромагнитный момент М = М_о уравновешивается внешним вращающим моментом, приложенным к валу машины. Тогда при колебаниях

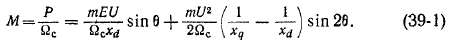
представляет собой значение М по формуле (39-1) при б = 6₀, а

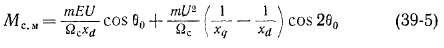в соответствии с (35-19) является коэффициентом синхронизирующего момента. При этом принимается, что ввиду малой амплитуды колебаний скорость вращения Q_c = const.

Так как М_о уравновешивается приложенным к валу внешним моментом, то достаточно учесть лишь второй член (39-3), который представляет собой известный из (35-4) синхронизирующий момент

и играет при этом роль, аналогичную упругой силе колеблющейся пружины с грузом. Знак минус в выражение (39-6) введен в связи с тем, что при Л4_С._М > 0 и Ае > 0 момент Л4_С действует на вал тормозящим образом, как это следует, например, из изложенного в § 35-3 и 35-4.

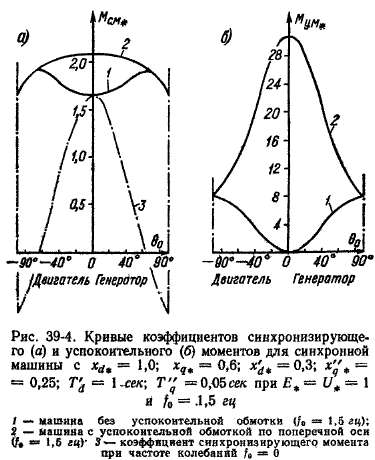
Необходимо отметить, что выражение (39-5) для М_с. _м действительно только при чрезвычайно медленных изменениях угла б, когда можно пренебречь электромагнитными переходными процессами в обмотках машины. В действительности скорость колебаний конечна, и поэтому в обмотках индуктора возникают такие же дополнительные апериодические токи, как и при внезапном коротком замыкании (см. § 34-3). Действие этих токов подобно действию тока возбуждения if₀, создаваемого напряжением возбудителя, что эквивалентно некоторому увеличению Е или уменьшению^ в равенстве (39-5). Вследствие этого при переходных процессах и, в частности, при колебаниях значение УИ_С. _м в действительности больше значения, определяемого равенством (39-5). На рис. 39-4, а в качестве примера приведены кривые М_с, _м = / (?о) Д^ля явнополюсной машины при колебаниях с частотой /₀ = 1,5 гц. Там же для сравнения изображена кривая М_с. _м, построенная по равенству (39-5) для случая, если бы колебания совершались чрезвычайно медленно (/₀ = 0). На рис. 39-4, а отложена относительная величина коэффициента синхронизирующего момента

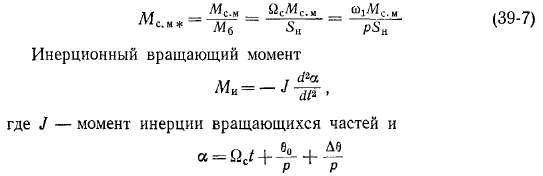
представляет собой угловую координату движения ротора, Угол а выражается в геометрических единицах угла, и поэтому электриче-

где первый ялен представляет собой угол поворота вектора В за время dt, а второй — угол поворота вектора U за это же время. Отсюда

Можно показать, что в случае, когда ротор синхронной машины в электрическом отношении полностью симметричен, как и ротор асинхронной машины, для М_у_ _м действительно выражение для вращающего момента асинхронной машины (25-6), если заменить в нем s на отношение /₀//_х. В действительности такая симметрия отсутствует, и поэтому М_у. _м зависит от положения осей симметрии ротора относительно волны поля реакции якоря, т. е. от угла в©.

Как следует из равенства (39-9), М_у. _м имеет размерность момента, умноженного на время. При переходе к относительным единицам за базисное следует принимать значение М_у. _м при М_г = Ms, и тогда

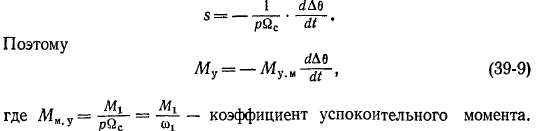
имеющие вид

Первый член под корнем выражения (39-13) обычно значительно меньше второго, и поэтому квадратный корень представляет собой мнимое число. Это и является условием возникновения колебательного процесса, так как при вещественном корне изменение Дб будет апер иодическим.

Согласно сказанному, вместо (39-13) можно написать

представляет собой постоянную времени затухания колебаний, а

— угловую частоту свободных, или собственных, колебаний синхронной машины.

При подстановке К_х и Х₂ из (39-14) в (39-12) получим

Согласно равенствам (39-15) и (39-17), колебания затухают тем быстрее, чем больше М_у. „. При УИ_у> „ = 0 постоянная времени Т_к — оо и колебания являются незатухающими.

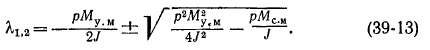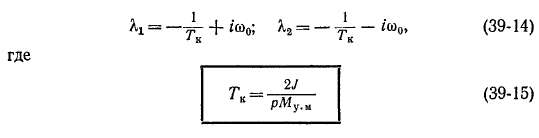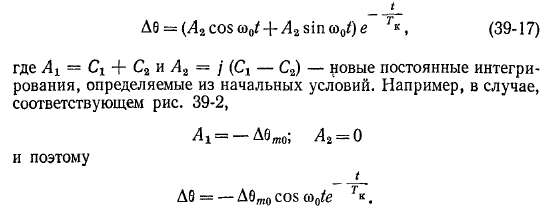
Самораскачивание синхронной машины. В случае когда My. м < О ^И поэтому на основании выражения (39-15) Т_к < О, в соответствии с (39-17) сколь угодно малые колебания, возникшие в результате каких-либо возмущений, будут не затухать, а возрастать по амплитуде. Такие случаи возникают на практике в маломощных синхронных машинах, не имеющих успокоительной обмотки, при работе параллельно с сетью на холостом ходу или при весьма малой нагрузке. При этом б о » 0 и, согласно рис. 39-4, б, также М_{у м} « 0. Однако кривые рис. 39-4 учитывают только успокоительный момент, который создается токами, индуктируемыми в обмотках ротора, при сопротивлении обмотки якоря г_а = 0. Как показывает более подробный анализ этого вопроса, при г_а ф- 0 создается еще небольшая дополнительная составляющая УИ_у. _м, которая отрицательная и по абсолютной величине тем больше, чем больше г_а. При этом в области бо ж 0 результирующая величина М_у_ „ у малых машин, которые имеют повышенные значения г_а, становится отрицательной и возникают самопроизвольные колебания, или так называемое самораскачивание машины. Амплитуда колебаний, достигнув определенной величины, обычно стабилизируется в результате наличия нелинейных зависимостей. У машин с Р_н > 10 -г- 20 кет самораскачивания обычно не наблюдается как ввиду малости г_а, так и в результате того, что и при расслоенных полюсах в сердечнике ротора индуктируются вихревые токи, создающие положительный успокоительный момент.

§ 39-3. Динамическая устойчивость синхронной машины

Под динамической устойчивостью синхронной машины понимается ее способность сохранять синхронный режим параллельной работы с сетью при больших и резких возмущениях режима ее работы (короткие замыкания в сети и пр.). Устойчивость работы при этих условиях зависит как от величины возмущения и его длительности, так и от параметров машины, величины, ее предшествующей нагрузки и прочих условий. В большинстве случаев при таких возмущениях возникают колебания или качания ротора с большой амплитудой. Нередко возникающий при таких возмущениях режим работы является неустойчивым и машина выпадает из синхронизма.

Вопросы, связанные с динамической устойчивостью, весьма сложны и рассматриваются подробнее в специальных курсах [69—79]. Ниже дается лишь понятие о динамической устойчивости.

Э. д. с. за переходным сопротивлением и угловая характеристика мощности при переходных режимах. При резких изменениях режима работы синхронной машины, как и при внезапных коротких замыканиях, в обмотках индуктора возникают добавочные апериодические токи, в результате чего э. д. с. Е, индуктируемая в обмотке якоря, увеличивается и угловая характеристика активной мощности, выражаемая равенством (35 4), изменяется. Как видно из (35-4), при этих условиях машина в состоянии развить большую электрическую мощность. Хотя равенством (35-4) можно пользоваться и при переходных режимах, но это неудобно, так как при этом каждый раз необходимо определять Е с учетом влияния апериодических токов в обмотках индуктора. Поэтому целесообразно такое

изменение соотношения (35-4), чтобы в него входили величины, которые при резких изменениях режима остаются неизменными.

Как было установлено в гл 34, при резких изменениях режима в обмотках возбуждения и успокоительной возникают апериодические токи, затухающие с постоянными времени T'_d и T"_d, Так как. период собственных колебаний Т_о = = 0,5 -*- 2,0 сек, T'_d = 0,5 ч- 3,0 сек и T"_d = 0,02 -f- 0,10 сек, то отсюда следует, что быстро затухающие апериодические токи затухают уже в самом начале первого периода колебаний и поэтому мало влияют на эти колебания. Следовательно, этими токами можно пренебречь. Однако T'_d > Т₀/2, поэтому медленно затухающие апериодические токи ротора в течение первого полупериода колебаний изменяются мало и в течение этого времени их можно считать постоянными. Изложенное равнозначно предположению, что в течение начального периода колебаний T_d — 0 и T'_d — оо. З^го соответствует случаю, когда успокоительная обмотка отсутствует, а обмотка возбуждения является сверхпроводящей и поэтому ее потокосцепление постоянно. Сопротивление успокоительной обмотки по поперечной оси г также велико, и поэтому можно положить, что Т"_щ — 0. Исходя из этих положений, можно преобразовать равенство (35-4), которое будет действительно для начального периода колебаний при резких изменениях режима работы синхронной машины.

Учитывая, что Е = x^if, согласно векторной диаграмме рис. 33-2, для установившегося режима действительно соотношение

Оно действительно и для начального периода резкого нарушения режима, если учесть увеличение if в результате возникновения свободной апериодической составляющей этого тока.

С другой стороны, условие постоянства потокосцепления обмотки возбуждения ¥f можно написать в следующем виде:

Отсюда

и это выражение также действительно как до, так и после резкого нарушений режима. Подставив это значение if в (39-23), находим

Обозначим первый ч,лен этого выражения, который вследствие постоянства потокосцепления W. также постоянен, через E'_d. С другой стороны, коэффициент второго члена

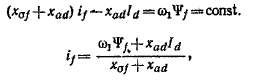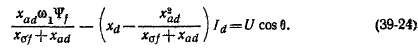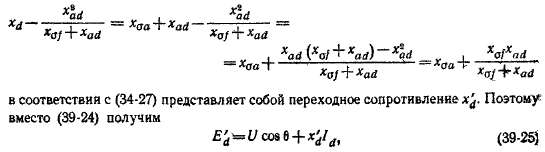
причем E'_d— const и соотношение (39-25) также действительно до и после нарушения режима.

Величину э. д. с. E'_d, называемой э. д.'с. за переходным сопротивлением x'_d, можно на#ти, построив векторную диаграмму э. д. с. по

данным предшествующего режима (рис. 39-5). Построив на этой диаграмме векторы x'_d\_d и Е'д, получим видоизмененную диаграмму, отличающуюся от обычной только заменой x_d на x'_d и Е на E'_d. Поэтому и выражение для угловой характеристики полу-

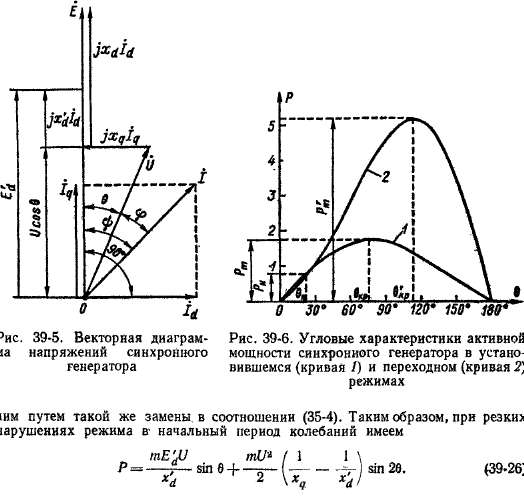Так как x'_d < х , то множитель перед sin 26 в данном случае отрицателен. На рис. 39-6 представлены зависимости Р — f (в) п© (35-4) (кривая У) и по (39-26) (кривая^.2) для явнополюсноймашины с x_d+= 1,1, х _# = 0,75, x'_dt = 0,25 при 1/„ = 1, когда машина в установившемся режиме работала с номинальной нагрузкой (cos ф_н = 0,8 (инд.), P_t = 0,8, б _н = 22°27'), чему соответствует Е# = = 1,87 и E'_dt = 1,14.

Из рис. 39-6 следует, что в переходном режиме машина при такой же величине U может нести значительно большую нагрузку, тем большую, чем меньше x'_d. Поэтому, чем меньше x'_d, тем больше динамическая устойчивость машины.

Понятие о динамической устойчивости. Рассмотрим случай (рис. 39-7), когда генератор Г, эквивалентный мощной электростанции, работает через трансформаторы Т1 и Т2 и две параллельные линии передачи Л1 и Л2~~на приемную

систему ПС с U= const. При установившемся режиме генератор работает в точке 1 угловой характеристики а рис 39-8, а, определяемой равенством (35-4), причем в данном случае параметры x_d, х , х'д включают в себя также индуктивные сопротивления трансформаторов и линий передачи. В точке / мощность генератора Р равна мощности Р_п. _д, развиваемой турбиной.

Допустим теперь, что в результате какой-либо неисправности одна из параллельных линий отключается. В результате такого динамического нарушения

режима наступает переходный процесс, в начальной стадии которого величина E'_d, определяемая параметрами и другими величинами исходного режима, остается постоянной. При этом будет справедливо соотношение (39-26), но вследствие отключения одной линии x'_d увеличится, и в резуль-

Рис. 39-7. Схема передачи энергии от синхронного генератора

тате этого угловая характеристика

переходного режима б рис. 39-8, а может пойти ниже характеристики а, несмотря на отмеченную выше способность машины развивать в переходном режиме при тех же U а х большую мощность. Угол 8 вследствие инерции мгновенно измениться не может, и поэтому непосредственно вслед за отключением линии генератор переходит на работу в точку 2 характеристики б. Так как мощность

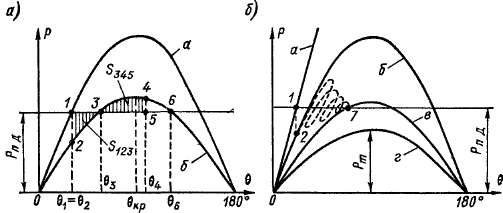Рис. 39-8: Угловые характеристики синхронного генератора в нормальных и аварийных режимах

турбины остается постоянной, то при этом Р > Р_п. _д поэтому ротор будет ускоряться и угол 6 будет расти. В точке 3 наступит равновесие мощностей Р = Р_п. _д и вращающих моментов, но угловая скорость Q будет больше синхронной Q_c, и поэтому в продолжает увеличиваться. Вправо от точки 3 будет Р>Р_и. _д, поэтому ротор будет тормозиться, Q — уменьшаться и на рис. 39-8, аъ некоторой точке 4 скорость уменьшится до синхронной Q = fl_c.

Положение точки 4 определяется равенством площадей заштрихованных треугольников 123 и 345, т.е S_4SS—S^4s (правило площадей). Действительно, длины линий штриховки этих треугольников пропорциональны неуравновешенному синхронизирующему моменту:

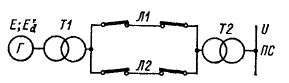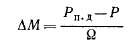
и работа dA, совершаемая этим моментом при изменении угла на d&, равная

идет на сообщение ротору во время его ускорения добавочной кинетической энергии этой же величины. Поэтому на участке кривой 1—3 ротор получает добавочную кинетическую энергию

Здесь мы положили Q « й_с так как эти величины мало отличаются друг от друга.

Аналогично при торможении ротора на участке 3—4 его кинетическая энергия уменьшается на величину S345 /рйс ^и поэтому скорость ротора достигнет синхронной, когда S₁₂g -- S&jb-

Таким образом, в точке 4 будет Q = Q_c, но так как Р > Р_п, _д, то торможение ротора продолжается, Q становится меньше Q_c и 6 уменьшается. При этом режим работы меняется от точки 4 к точке 3, в точке 3 Р = Р_п. _д и торможение прекращается, но при этом Q < Й_с, уменьшение в поэтому будет продолжаться и режим меняется от точки 3 к точке 2. На этом участке Р_п. _д < Р, поэтому будет происходить ускорение ротора, Q будет расти, но уменьшение 6 будет продолжаться до тех пор, пока в точке 2 не станет Й = Q_c. Этим заканчивается первый период колебаний ротора и угла 8 от 8 = 6₂ до 9 = б₄ и обратно до 6 = 8₂. После этого ротор снова начинает ускоряться, рассмотренный цикл колебаний повторяется и наступают незатухающие колебания ротора с колебаниями 8 в диапазоне 6₂ — 6₄. Машина при этом из синхронизма не выпадает, хотя очевидно, что наибольший угол 6₄ может быть больше 8_кр.

К заключению о возникновении незатухающих колебаний мы пришли потому, что полагали E'_d = const и неизменность в связи с этим характеристики б рис. 39-8, а во время колебаний и, кроме того', пренебрегли успокоительным моментом My, возникающим в результате того, что Q ф Q_c. В действительности даже при предположении Е^ = const момент М ^0 и машина развивает мощность также за счет этого момента. Поэтому при движении от точки 2 на рис. 39-8, а к точке 4, когда Q > Q_c и s < 0 (режим асинхронного генератора), характеристика Р ⁼ / (в) пойдет несколько выше кривой б, ускорение на участке 2—3 будет слабее, а торможение на участке 3—4 — сильнее и в результате угол B_i будет несколько меньше. Далее, при движении от точки 4 к точке 2, когда Q < Q_c и s > 0 (режим асинхронного двигателя), характеристика Р = / (8) пойдет ниже кривой б, вследствие этого на участке 4—3 торможение вниз от Q = Q_c будет слабее, а на участке 3—2 ускорение будет сильнее и поэтому равенство Q = Q_c после первого периода колебаний наступит правее точ'ки 2. Таким образом, под воздействием М_у размах, или амплитуда, колебаний будет беспрерывно уменьшаться до тех пор, пока эти колебания не затухнут полностью и при E'_d — = const не наступит установившийся режим работы в точке 3, когда Р = Р_п, _д. Характер колебаний при этом имеет вид кривых на рис. 39-2 и 39-3.

На самом деле предположение E'_d = const с достаточной точностью действительно только для первого полупериода колебаний, от точки 2 до точки 4 на рис. 39-8, а. В дальнейшем наступает заметное затухание всплеска тока возбуждения Л/., вызванного динамическим нарушением режима, и поэтому E'_d будет уменьшаться. Вследствие этого ординаты кривой б будут беспрерывно уменьшаться и при Д(^=0 характеристика Р = / (9) изобразится в виде

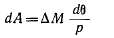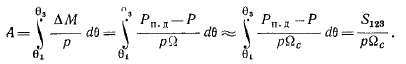
кривой в на рис. 39-8, б, которая соответствует равенству (39-4) и расположена ниже кривой а, так как при отключении одной линии на схеме рис. 39-7 х# и х„ увеличатся. Поэтому колебания в действительности происходят вдоль штриховой кривой рис. 39-8, б и установившийся режим наступает в точке 7 кривой в. Колебания при этом также имеют характер, изображенный на рис. 39-2 и 39-3. Однако если, согласно выражению (35-4), установившемуся режиму вместо кривой в рис. 39-8, б будет соответствовать кривая г этого же рисунка, то машина, сохраняя синхронизм в течение первого периода колебаний, выйдет из синхронизма в течение последующих циклов колебаний, так как максимальная развиваемая мощность генератора Р_т < Р_п. _д. Угол 9 при этом будет беспредельно расти (рис. 39-9, а).

Может случиться также, что кривая б на рис. 39-8, а будет располагаться настолько низко, что площадь S^ будет больше площади S$jgg фигуры 3465, на-ходящейся над прямой Р_п. _д = const. Тогда площадь торможения S$ig$ будет не--достаточна и, хотя на участке 346 ротор тормозится, в точке 6 скорость Q будет

Рис. 39-9. Графики изменения угла нагрузки при выпадении синхронной машины из синхронизма в процессе колебаний (а) и во время первого полупериода колебаний (б)

еще больше синхронной й_с и угол 8 в точке 6 будет продолжать увеличиваться. Поэтому изменение режима будет происходить вправо от точки 6, при этом 8 > 8_g и Р < Р_п. д. В результате вновь наступит ускорение :ротора, угол в будет беспрерывно расти, машина выпадет вд синхронизма и перейдет в возбужденный асинхронный режим работы, когда генераторные режимы будут чередом ваться с двигательными. В этом случае выпадение из синхронизма произойдет в первом цикле колебаний и характер функции 8 — / (Q будет иметь вид рис, 39-9,6

Выше мы предполагали, что величина тока возбуждения fy₀ во время динамических нарушений не регулируется. Ясно, однако, что если в самом начале динамического нарушения i ,_fl быстро увеличить, то Е и E'_d увеличатся и поэтому кривые б/, в, г на рис. 39-9, а и б расположатся выше. Во-первых, при этом уменьшится амплитуда колебаний угла в.

I Во-вторых, при достаточно большом увеличении i/_e можно избежать выпадения машины из синхронизма.

Кроме того, нетрудно заключить также, что целесообразно регулировать, величину tf₀ во время колебаний в зависимости от изменения в. При этом, например, во время первого полупериода колебаний, при изменении угла 8 на рис. 39-8, а от 8 = 8j до 9 = В₄, надо i/_e увеличивать, а во время второго полу* периода, от точки 4 до точки 2, — уменьшать. При этом размах колебаний # уменьшится.

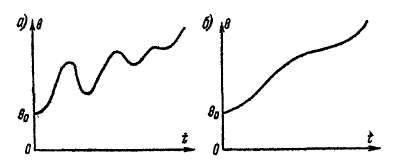
При подобном же регулировании ip в последующих циклах колебаний можно достичь быстрого успокоения колебаний. Подобное же регулирование возбуждения эффективно для уменьшения амплитуды вынужденных колебаний синхронных двигателей и генераторов, соединенных с поршневыми машинами Вследствие малости периода колебаний и быстротечности переходных процессов регулирование if₀ также должно совершаться быстро, с помощью автоматических регуляторов тока возбуждения.

Содержание
Предыдущий § Следующий