Содержание
Предыдущий § Следующий

Глава двадцать пятая ВРАЩАЮЩИЕ МОМЕНТЫ И МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ АСИНХРОННОЙ МАШИНЫ

§ 25-1. Электромагнитный момент

Выражение для электромагнитного момента. Электромагнитный момент, развиваемый электромагнитными силами на роторе асинхронной машины, определяется-*равенством

где Р_мХ — механическая мощность на роторе, определяемая выражением (2^-74), й — механическая угловая скорость вращения ротора.

Механическая угловая скорость вращения магнитного поля основной гармоники

Таким образом, на основании равенств (25-4) и (25-5)

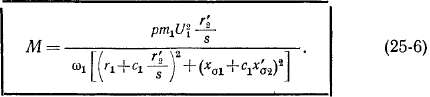При пользовании единицами системы СИ момент М по формуле (25-4) и (25-6) выражается в ньютон-метрах. При желании иметь М в килограмм-метрах необходимо разделить результат на 9,81 -

Согласно выражению (25-6), электромагнитный момент при любом заданном значении скольжения пропорционален квадрату приложенного напряжения и тем меньше, чем больше г_г и индуктивные сопротивления рассеяния машины. В соответствии с формулой (25-4) при любом заданном s величина М пропорциональна также квадрату вторичного тока.

Исследуем зависимость М = f (s) при XJ_X — const.

Согласно равенству (25-6), при s>0 также М > О (режимы двигателя и противовключения)^ а при s < 0 тЗкже М <. О (режим генератора). Кроме того, при s = О также М = О, что можно установить по формуле (25-6) путем раскрытия неопределенности или пренебрегая в квадратных скобках этой формулы при s -»• 0 всеми

г' членами, кроме с-^-^-. Эти результаты были установлены уже ранее

(см. § 24-4 и 24-5) на основе физических соображений. Помимо этого, в соответствии с (25-6) при s = +оо будет М = 0. Последнее объясняется тем, что, согласно выражению (24-18), при s = сю ток /₂ является чисто реактивным и поэтому не развивает вращающего момента.

Поскольку в точках s = —оо, 0 и + оо момент М = 0, то между этими точками находятся экстремумы (максимум и минимум) момента.

На основании изложенного кривая М — f (s) при U = const имеет вид, изображенный на рис. 25-1. На этом же рисунке показана кривая 1'ч = f (s), построенная по соотношению (25-5), и кривая первичного тока 1_г = f (s). Все эти кривые даны в относительных единицах и соответствуют асинхронной машине мощностью Р_н = = 15 кет при U_± = U_la и при условии независимости параметров машины от величин токов и скольжения. Вместо s на оси абсцисс можно откладывать также скорость вращения ротора п = (1 — s)n_v

Из рис. 25-1 видно, что электромагнитный момент достигает отрицательного и положительного максимумов ± М_т при некоторых скольжениях s = ±s_m, которые называются критическими.

При увеличении скольжения от s = 0 до s = s_m момент М растет вместе с увеличением s, а при дальнейшем увеличении скольжения момент М уменьшается, несмотря на увеличение Г_г. Такой ход кривой М = f (s) объясняется тем, что с увеличением s ток /г становится по своему характеру все более индуктивным. Поэтому активная составляющая 1'_%, которая определяет величину М, при увеличении s сначала растет вместе с /£, а затем начинает уменьшаться, несмотря на увеличение I'_t. Следует также учитывать, что с увеличе-

Рис 25-1 Кривые электромагнитного момента и токов асинхронной машины

нием /j падение напряжения в первичной цепи увеличивается, а соответственно этому э. д с. Е_х и поток Ф, во взаимодействии с которым создается момент, несколько уменьшаются.

Необходимо отметить, что на статор электрической машины действует такой же вращающий момент, как и на ротор, но направленный в противоположную сторону.

Момент, действующий на статор, воспринимается деталями й узлами, крепящими машину к фундаменту.

Электромагнитный момент как результат взаимодействия пространственных волн магнитной индукции и токов. В § 22-4 пространственное распределение тока обмотки вдоль окружности якоря было представлено в виде суммы синусоидальных пространственных волн тока разных гармоник.

Возникновение в электрической машине электромагнитных сил и вращающих моментов можно рассматривать как результат взаимодействия указанных волн тока с синусоидальными же волнами распределения индукции магнитного поля вдоль окружности якоря. Отличный от нуля вращающий момент

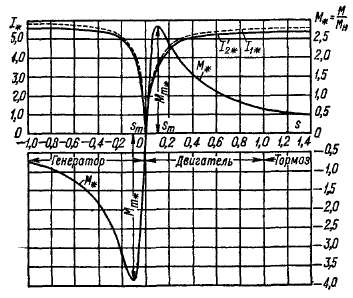
создается взаимодействием пространственных гармоник тока и магнитного поля одинакового порядка, а гармоники разных порядков создают вдоль окружности якоря знакопеременные электромагнитные силы и составлящие момента, суммарная величина которых равна нулю.

На рис. 25-2, а показана кривая индукции основной гармоники результирующего магнитного поля в зазоре асинхронной машины

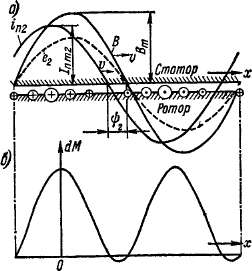Рис. 25-2. Образование вращающего момента как результат взаимодействия пространственных волн магнитной индукции и тока

Подставив значения этих величин в (25-10), получим выражение для М в другой форме:

На основании выражения (25-11) момент пропорционален потоку машины и активной составляющей тока /^ или /₂, что вполне согласуется с основными физическими представлениями об электромагнитных силах и находится в соответствии с изложенным выше.

Согласно выражениям (24-6) и (24-18),

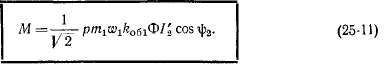При подстановке этих величин в (25-11) получим соотношение (25-4). Отсюда следует вывод, что выражения (25-4) и (25-11) вполне равноценны.

Максимальный электромагнитный момент. Выражение для электромагнитного момента (25-6) верно в общем случае, т. е. также тогда, когда параметры г_ъ х_а1, г'%, х'_а2 не постоянны и зависят от величин токов и скольжения. В этом случае при каждом значении s в выражение (25-6) нужно подставлять соответствующие значения указанных параметров. Ограничимся здесь рассмотрением машины с постоянными параметрами и исследуем зависимость М = f (s) по формуле (25-6) при U_x = const и /₂ = const на максимум и минимум.

Вместо s удобнее рассматривать переменную величину

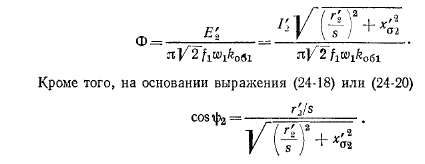
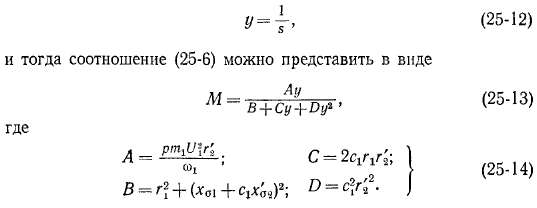
Взяв от (25-13) производную по у и приравняв ее нулю, получим уравнение для определения значений у = у_т, при которых М имеет экстремумы:

В этих соотношениях знаки плюс относятся к двигательному, а знаки минус — к генераторному режиму работы.

Для нормальных асинхронных машин члены с г_х в выражениях (25-17) и (25-19) малы по сравнению с остальными. Полагая поэтому г_х = 0, имеем

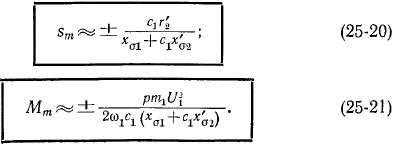
Полученные соотношения позволяют сделать вывод, что величина максимального момента, во-первых, не зависит, согласно выражениям (25-19) и (25-21), от величины активного сопротивления вторичной цепи, во-вторых, пропорциональна квадрату напряжения, в-третьих, с большой точностью обратно пропорциональна индуктивным сопротивлениям рассеяния и, в-четвертых, в генераторном режиме несколько больше, чем в двигательном. Так как и_г ^ ДФ, то из выражения (25-21) можно сделать также вывод, что максимальный момент пропорционален квадрату магнитного потока машины. Весьма важно подчеркнуть, что, хотя момент М_т не зависит от вторичного активного сопротивления, величина скольжения s_m, при котором наблюдается этот момент, согласно выражениям (25-17) и (25-20), пропорциональна этому сопротивлению.

У асинхронных двигателей нормального исполнения кратность максимального момента при номинальном напряжении

и s_m = 0,06 -f- 0,15. Более высокие k_m имеют двигатели с малым числом полюсов.

Применим соотношение (25-4) для номинального режима работы (индекс «н») и для режима с максимальным моментом (индекс т).

Обычно у асинхронных двигателей это отношение находится в пределах 2,5—3,5.

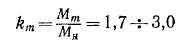
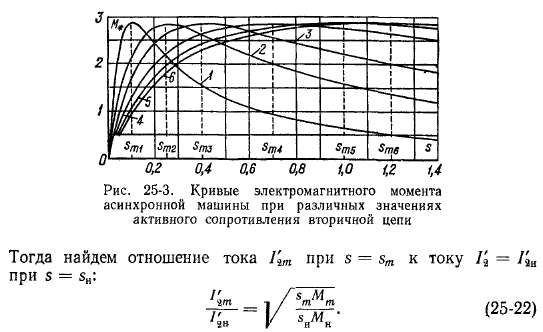
В качестве иллюстрации к изложенному на рис. 25-3 представлены кривые М = / (s) для разных значений rjj в двигательном режиме работы той же асинхронной машины мощностью 15 кет, как и на рис. 25-1. Отметим, что величина г\ включает в себя как активное сопротивление самой вторичной обмотки, так и сопротивление реостата, который может быть включен во вторичную цепь машины с фазным ротором. Кривая / на рис. 25-3 соответствует нормальному значению г!_г вторичной обмотки, а остальные кривые — повышенным значениям г\ или случаю включения реостата во вторичную цепь.

Величина электромагнитного момента по отношению к его максимальному значению. Для отношения этих моментов для машины с постоянными параметрами может быть получено простое выражение, удобное для некоторых практических расчетов.

Из уравнения (25-16) находим

При s_m — 0,15 ч- 0,30 ошибка в определении М1М_т по приближенной формуле (25-25) составляет около 10—17%.

Формула (25-25) впервые была выведена М. Клоссом. В связи с этим формулы (25-23) и (25-25) называются формулами Клосса.

Формула (25-25) позволяет определить М_т и s_m и построить кривую М — f (s) для двигателя с постоянными параметрами, если известны М и s для каких-либо двух режимов работы, например для номинального (УИ_Н, s_H) и пускового (М_ш, s_H = 1). Более точная кривая М = f(s) может быть построена по уравнению (25-23), если известно также значение а по формуле (25-24). Приближенно можно принять а = 2.

Начальный пусковой электромагнитный момент М_п соответствует значению электромагнитного момента в начальный момент пуска двигателя, т. е. при s = 1. Согласно выражению (25-6),

I Пусковой момент при данных значениях параметров машины также пропорционален квадрату приложенного напряжения.

Из выражения (25-26) и рис. 25-3 следует, что с увеличением т\ момент М_п растет до тех пор, пока при s_m = 1 не будет М_п = М_т. При этом, согласно равенству (25-17),

При дальнейшем увеличении г'₂ момент М_п будет снова уменьшаться. В то же время пусковое значение тока

Е-* 2JS-1 = ^2П

при увеличении г'₂, согласно выражению (25-5), беспрерывно уменьшается. Увеличение М_а, несмотря на уменьшение /^ при увеличении г'% до значения, определяемого равенством (25-27), объясняется тем, что при этом уменьшается угол сдвига г|)₂ между током Г* и э. д. с. £₂.

§ 25-2. Механическая характеристика асинхронного двигателя и эксплуатационные требования к ней

Полезный вращающий момент на валу двигателя М₂ меньше электромагнитного момента М на величину

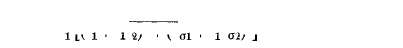
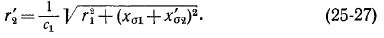
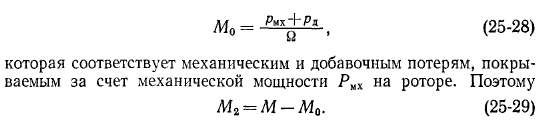
Механическая характеристика двигателя представляет собой зависимость скорости вращения п от развиваемого момента на валу М_г при U_x = const и f_x = const:

Так как при нагрузке момент М_о мал по сравнению с М и М₂, то можно положить М_о « 0 или включить М_о в величину статического тормозящего момента М_ст, который развивается рабочей машиной или механизмом, приводимым во вращение асинхронным двигателем. Поэтому ниже в качестве механической характеристики двигателя будем рассматривать зависимость между п (или s) и электромагнитным моментом М:

Изображенные на рис. 25-1 и 25-3 кривые момента М при указанных условиях и представляют собой механические характеристики асинхронного двигателя с постоянными параметрами.

I Очевидно, что вид механических характеристик существенно зависит от величины вторичного активного сопротивления.

Процесс пуска и установившийся режим работы асинхронного двигателя. Рассмотрим процесс пуска асинхронного двигателя с ко-роткозамкнутой вторичной обмоткой при его включении на полное напряжение сети. Так производится пуск подавляющего большинства находящихся в эксплуатации асинхронных двигателей. При рассмотрении процесса пуска не будем принимать во внимание электромагнитные переходные процессы, связанные с тем, что при включении любой электрической цепи электромагнитного механизма под напряжение и при изменении режима его работы токи достигают практически установившихся значений не сразу, а после истечения некоторого времени, величина которого пропорциональна электромагнитной постоянной времени Т, зависящей от индуктивности и активного сопротивления цепи. Обычно при пуске асинхронного двигателя время его разбега до нормальной скорости значительно больше длительности электромагнитных переходных процессов, и поэтому влияние этих процессов на процесс пуска невелико. Следовательно, процесс пуска можно рассматривать на основе полученных выше зависимостей для вращающего момента и токов в условиях работы двигателя при установившемся режиме с заданным скольжением.

На рис. 25-4 показана механическая характеристика М = f(n) асинхронного двигателя и механическая характеристика М_ст = f (n)

некоторого производственного механизма, приводимого во вращение двигателем.

Уравнение моментов агрегата «двигатель — производственный механизм» имеет вид

представляет собой динамический вращающий момент агрегата, пропорциональный моменту его инерции J. Если при п = О, как

При этом УИд_ИН = 0, ^ = 0 и наступает установившийся режим

работы двигателя под нагрузкой со скоростью вращения п' и скольжением s'. Величина s' будет тем больше, чем больше УИ_СТ и чем больше, следовательно, нагрузка двигателя. Если при работе двигателя его нагрузку (статический, момент производственного механизма М_ст) увеличить (кривая 2 на рис. 25-4), то s возрастет, а п уменьшится. При уменьшении нагрузки (кривая 3 на рис. 25-4), наоборот, s уменьшится, а я увеличится.

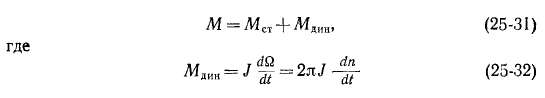
Переход двигателя к новому установившемуся режиму работы при изменении нагрузки физически происходит следующим образом. Если М^ возрастет, то будет М < М_ст, М_дин < 0, -£ < 0 и

движение ротора двигателя станет замедляться. При этом скольжение возрастает, в соответствии с чем увеличиваются также э. д. с. £_2S и ток /₂ вторичной цепи. В результате электромагнитный момент М увеличивается и уменьшение п (увеличение s) происходит до тех пор, пока снова не наступит равенство моментов М = М„. При уменьшении нагрузки процесс протекает в обратном направлении.

Как видно из рис. 25-4, при круто поднимающейся начальной (левой) части кривой момента М = f (s) асинхронный двигатель обладает жесткой механической характеристикой, т. е. при изменении нагрузки скорость вращения двигатедя изменяется мало. Все нормальные асинхронные двигатели строятся с жесткой механической характеристикой, когда г'_% и s_m относительно малы. При этом s и, следовательно, р_эл2 [см. равенство (24-72)] при работе также малы и двигатель имеет высокий к. п. д.

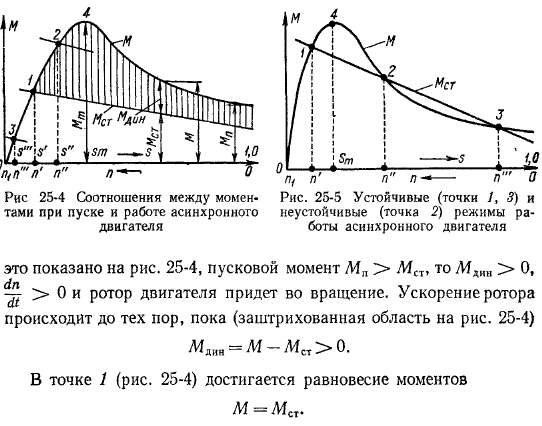
Условия устойчивой работы. В общем случае, как показано на

рис. 25-5, характеристики двигателя М = f (n) и производственного механизма М„ = / (п) могут иметь несколько точек пересечения.

В точках / и 3

А АЛ АЛЛ

(25-33)

и работа неустойчива.

При пуске из неподвижного состояния двигатель достигает устойчивой скорости вращения в точке п'" (рис. 25-5) и дальнейшее увеличение п невозможно, так как влево от этой точки М„ > М. Если бы двигатель работал в режиме; соответствующем точке 2 (рис. 25-5), то при малейших нарушениях режима и изменении п соотношения между М и М_сг стали бы такими, что двигатель перешел бы на работу в режиме, соответствующем одной из устойчивых точек / или 3. Режим работы в точке 3 на практике неприемлем, так как характеризуется малой скоростью вращения, плохим к. п. д. и наличием больших токов в обмотках, вследствие чего двигатель

быстро перегревается и выходит из строя. Поэтому нормальной устойчивой областью работы двигателя считается участок механической характеристики влево от точки 4 (рис. 25-4), когда 0 < s < <s_m.

Перегрузочная способность асинхронного двигателя. При работе двигателя на нормальном устойчивом участке механической характеристики (влево от точек 4 на рис. 25-4 и 25-5) его нагрузку, определяемую статическим моментом М„ рабочего механизма или машины, можно постепенно поднять до величины М_ст = М_т (точки 4 на рис. 25-4 и 25-5), причем устойчивая работа сохраняется вплоть до этой точки. При дальнейшем увеличении нагрузки, когда М_ст > > М_т, двигатель будет быстро затормаживаться и либо остановится, либо при характеристиках вида рис. 25-5 перейдет в устойчивый режим работы при малой скорости вращения. В обоих случаях, если двигатель не будет отключен, возникает опасный в отношении нагрева режим.

Таким образом, в принципе работа асинхронного двигателя возможна при 0 < М •< М_т. Однако продолжительная работа при М яа М_т в отношении нагрева также недопустима.

Кроме того, при работе двигателя необходимо иметь некоторый запас по моменту, так как возможны кратковременные перегрузки случайного характера, а также кратковременные или длительные понижения напряжения сети.

Так как М_т я» V\, то при уменьшении U_lt например, на 15% максимальный момент двигателя снизится до 0,85² = 0,72 или 72% от своего первоначального значения.

В связи с изложенным всегда должно быть М_т > М_я.

Отношение максимального момента при номинальном напряжении к номинальному

определяет перегрузочную способность двигателя и называется кратностью максимального момента. Согласно ГОСТ 186—52 и ГОСТ 9362—60, для двигателей разных мощностей и скоростей вращения требуется, чтобы k_m > 1,7 -г-2,2. Меньший предел относится к двигателям со скоростью вращения п ==с 750 об/мин.

Кратности начального пускового момента и пускового тока.

Часто асинхронные двигатели можно пускать в ход на холостом ходу или с малой нагрузкой на валу и нагружать их до номинальной или иной мощности после достижения нормальной скорости вращения. В других случаях рабочие механизмы и машины (например, вентиляторы) имеют механическую характеристику М_ст =

= / (п) такого вида, что при п = 0 статический момент М_ст мал и постепенно повышается с увеличением п. При этом не требуется, чтобы двигатель развивал большой пусковой момент. Однако иногда двигатели необходимо пускать в ход под значительной нагрузкой (например, крановые механизмы, подъемники, различные мельницы и т. д.), и в этих случаях требуется, чтобы двигатели имели большие пусковые моменты.

Асинхронные двигатели с фазным ротором можно пускать в ход с помощью реостата, включаемого на время пуска во вторичную цепь двигателя. Как следует из § 25-1 (см. рис. 25-3), при этом пусковой момент двигателя увеличивается, а пусковой ток уменьшается. Поэтому стандарты не регламентируют величин пусковых моментов и токов асинхронных двигателей с фазным ротором. В то же время выпускаемые электромашиностроительными заводами серийные асинхронные двигатели с короткозамкнутым ротором должны удовлетворять разнообразным условиям пуска производственных механизмов и их пусковые моменты должны быть достаточно велики.

Согласно ГОСТ 186—52 и ГОСТ 9362—60, короткозамкнутые асинхронные двигатели должны иметь при пуске под номинальным напряжением кратность начального пускового момента М„ (_S= 1, _п = 0)

не менее 0,7—1,8. Меньшие значения относятся к двигателям большей мощности. Кратность пускового тока

для двигателей с короткозамкнутым ротором разных мощностей и разных скоростей вращения при этом должна быть не больше 5,5-7,0.

Пригодность асинхронных двигателей с короткозамкнутым ротором и с постоянными параметрами в качестве двигателей общего назначения. Как уже указывалось, для получения хорошего к. п. д. асинхронные двигатели должны работать при номинальной нагрузке с малым скольжением (s = 0,02 ■*■ 0,05) и иметь, таким образом, жесткую механическую характеристику (s_m = 0,06 н- 0,15). Это требование для двигателей с короткозамкнутым ротором и с постоянными параметрами вступает в противоречие с требованием о достаточной величине пускового момента двигателя. Действительно, как видно из кривой / рис. 25-3, пусковой момент при этих условиях получается недостаточно большим. Это же можно установить по соотношению (25-25), если переписать его один раз для

режима пуска (s = 1, М = М„), другой раз — для номинального режима (s = s_H, M = М_н) и разделить получаемые соотношения друг на друга. При этом будем иметь

Таким образом, двигатели с постоянными параметрами развивают недостаточный пусковой момент. В связи с этим двигатели общего назначения с короткозамкнутым ротором строятся исключительно как двигатели с переменными параметрами. При этом для увеличения г'^ в период пуска и для увеличения тем самым М_п используется явление поверхностного эффекта или вытеснения тока £ обмотке ротора (см. гл. 27).

§ 25-3. Электромагнитные моменты и силы от высших гармоник магнитного поля

Выше рассматривался электромагнитный момент, создаваемый основной гармоникой поля. Наряду с основной гармоникой существуют также высшие и низшие гармоники поля, вызванные наличием гармоник н с. обмоток и зубчатым строением статора и ротора. Эти гармоники поля также создают вращающие моменты, которые можно подразделить на асинхронные и синхронные.

Вращающие моменты создаются тангенциальными электромагнитными силами. Кроме этих сил, действуют также радиальные электромагнитные силы, которые вызывают вибрацию и шум машины.

Указанные моменты и силы проявляются наиболее сильно при скольжениях, близких к единице, т. е. при пуске и торможении двигателя. Причина этого заключается, во-первых, в том, что при s = 1 токи велики. Во-вторых, высшие гармоники поля вращаются медленно и синхронная скорость вращения ротора для них мала, а моменты достигают максимальных значений вблизи их синхронной скорости.

Остановимся кратко на перечисленных явлениях.

Асинхронные моменты. Рассмотрим, например, седьмую гармонику поля статора(л> — 7), которая вращается в том же направлении, что и основная, со

скоростью щ = -=- п-у. При вращении этой гармоники относительно ротора в обмотке ротора индуктируются э-. д. с. и токи и создается вращающий момент M_lt так же как и в результате действия основной гармоники поля. В момент пуска, при s = 1, момент М₇ > 0 и действует согласно с моментом основной гармоники Mi (рис. 26-6). Когда ротор придет во вращение в сторону вращения основной гармоники (s < 1), относительная скорость поля седьмой гармоники и ротора начнет уменьшаться. При скорости ротора n = nj7 или s = 6/7 седьмая гармоника поля будет относительно него неподвижна и М_ч = 0 При дальнейшем увеличении п ротор вращается быстрее седьмой гармоники поля, по отношению к нему возникает генераторный режим работы и М₇ < 0 (рис. 25-6).

Пятая гармоника поля вращается в обратном направлении, и синхронное вращение ротора относительно нее наступает в тормозном режиме — при п =

= — nJ5 или s = 6/5. Кривая момента этой гармоники М_ъ также изображена на рис. 25-6.

Подобные же кривые моментов создаются другими гармониками поля, поэтому кривая результирующего момента

искажается (рис. 25-6) и в ней возникают провалы. При большой величине этих провалов и достаточно большом статическом моменте Л4_СТ на валу может наступить устойчивый режим работы при малой скорости вращения в процессе пуска двигателя (точка а на рис. 25-6) или при его торможении (точка б на рис. 25-6), в результате чего двигатель не достигает нормальной скорости вращения. При пуске опасным является действие прямых гармоник поля, а при торможении — обратных. Ввиду изложенного моменты от высших гармоник поля называются также паразитными.

Согласно ГОСТ 186—52, отношение минимального момента в процессе пуска к номинальному для двигателей мощностью 0,6—100 кет не должно быть меньше 0,8.

При фазной обмотке ротора искажение кривой моментов незначительно. Это, с одной стороны, объясняется тем, что ввиду малых значений обмоточных коэффициентов такой обмотки для высших гармоник поля индуктируемые гармоники э. д. с. невелики. С другой стороны, индуктивное сопротивление рассеяния такой обмотки для токов от высших гармоник поля велико. Это вызвано тем, что токи, индуктируемые v-й гармоникой поля статора в обмотке ротора, создают, кроме v-й Же гармоники, также гармонику v = 1 поля ротора, которая значительно больше гармоник и в данном случае по отношению к v-й индуктирующей гармонике составляет поле рассеяния.

Отметим, что высшие гармоники поля самого ротора в свою очередь индуктируют токи в обмотке статора и поэтому также создают паразитные моменты рассмотренного выше характера. Поскольку, однако, обмотка статора всегда является фазной, то эти моменты незначительны.

Реальную опасность моменты высших гармоник вызывают в случае коротко-замкнутой обмотки ротора, так как при этом для токов от высших гармоник поля могут создаваться короткие цепи, состоящие из соседних или близлежащих стержней и участков колец и обладающие весьма малым сопротивлением (рис. 25-7). Возможность образования таких цепей тем больше, чем больше число пазов ротора 1_%.

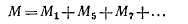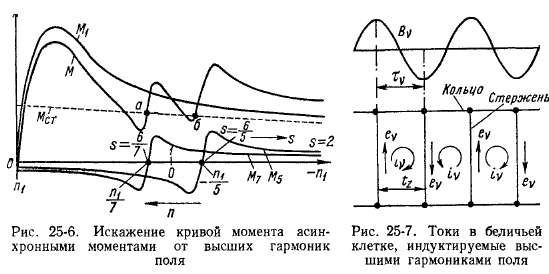
Наиболее сильными и опасными являются гармоники статора зубцового порядка (см. гл. 22 и § 23-1)

Поэтому отношение 1_г и 1^ не должно быть слишком большим. Более подробный анализ вопроса показывает, что во избежание значительного искажения кривой моментов необходимо брать

Кроме этого, эффективной мерой борьбы с вредным влиянием высших гармоник статора на кривую момента является скос пазов ротора на одно зубцовое деление статора, так как при этом э. д. с. в стержнях ротора от зубцовых гармоник статора снижаются почти до нуля (см. § 20-3). Однако при этом увеличиваются добавочные потери от поперечных токов, протекающих между соседними неизолированными стержнями через зубцы и спинку сердечника якоря. Поэтому в последние годы скоса пазов избегают и при крайней необходимости применяют скос до половины зубцового деления.

Как видно из рис. 25-6, в результате действия высших гармоник снижается, хотя и незначительно, также момент двигателя при нормальном режиме работы (s я; 0). Это отражается на к. п. д. двигателя.

Рассмотренные выше моменты высших гармоник называются асинхронными, так как они по своей природе совершенно одинаковы с основным электромагнитным моментом асинхронной машины, возникают в результате взаимодействия поля данной гармоники статора с токами (или магнитным полем) ротора, индуктированными (или созданным) этой же гармоникой поля статора, при любой данной скорости вращения ротора имеют определенную величину и направление действия, так как данная гармоника статора и вызванная ею такого же порядка гармоника-поля ротора вращаются всегда синхронно. Синхронные моменты возникают в результате взаимодействия таких гармоник полей статора и ротора, которые имеют одинаковый порядок v или одинаковые полюсные деления t_v, но созданы независимо друг от друга (как и магнитные поля статора и ротора синхронной машины), т. е. ни одна из них не является результатом действия другой. Такие гармоники поля вращаются относительно друг друга несинхронно и поэтому в зависимости от их взаимного положения в данный момент времени создают вращающий момент того или другого направления-или знака (см. рис. 25-8, где рассматриваемые гармоники статора и ротора условно изображены в виде магнитных полюсов и создают действующие на ротор силы F). При несинхронном вращении эти гармоники создают знакопеременный вращающий момент большой частоты, средняя величина которого равна нулю. Ввиду большой

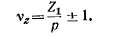
механической инерции ротора этот момент на движение ротора влияния не оказывает.

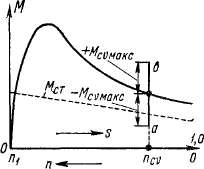
Однако при некоторой, вполне определенной скорости ротора п = n_cv такие гармоники могут вращаться синхронно, и при этом в зависимости от их взаимного положения создается положительный или отрицательный момент M_cv той или иной величины в пределах — M_cvmKc^ M_cv ^ + M_CVMaKz. Величина этого момента изобразится на кривой М = f(s) в виде определенной точки на вертикальном отрезке прямой аб (рис. 25-9). Из-за действия этого момента при пуске двигатель может «застрять» на скорости вращения «_cv и не «дойти» до нормальной скорости. Но в отличие от асинхронных моментов в данном случае имеется большая вероятность того, что ротор вследствие своей инерции перейдет через зону опасного действия синхронного момента. Поэтому, если синхронные моменты возникают при скорости п Ф О, то они менее опасны, чем асинхронные моменты.

Рассмотрим пример, когда синхронный момент создается гармониками зуб-цового порядка, которые являются наиболее сильными.

Пусть обмотка статора имеет т_х = 3, 1р = A, Z₁= 24, а короткозамкнутый ротор имеет Z₂ = 28. Тогда гармоники первого зуб-цового порядка, создаваемые током статора и током основной частоты f₂ = s/_t ротора, будут равны: прямая гармоника статора

Таким образом, одинаковый порядок имеют прямая гармоника статора и обратная гармоника ротора v'_zl = v"₂ = 13. Первая из них вращается относительно статора со скоростью nj\3, а вторая — относительно ротора со скоростью

Рис. 25-9. Искажение кривой

моментов синхронным моментом

от высших гармоник поля

откуда п = nj7, т. е. синхронный момент возникает в двигательном режиме во время пуска при скорости, равной одной седьмой синхронной скорости.

В рассматриваемом случае Z₂ — Ъ\ — 4 = 2р. Нетрудно видеть, что синхронные моменты возникают всегда в результате взаимодействия зубцовых гармоник первого порядка при вращении ротора при

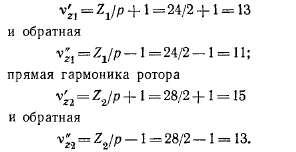
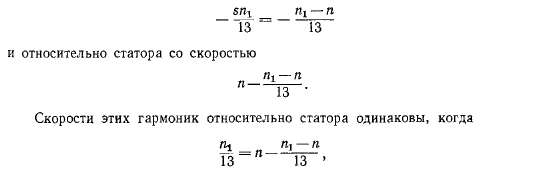
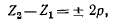
где знак минус соответствует возникновению синхронных моментов в тормозном режиме.

Если Z₂ =- Z_ly то порядки прямых зубцовых гармоник статора и ротора равны и гармоники вращаются синхронно в начальный момент пуска, при п = 0. Это же верно и для обратных зубцовых гармоник. Поэтому в данном случае образуются сильные синхронные моменты в неподвижном состоянии ротора и ротор не может сдвинуться с места.

Из сказанного следует, что во избежание значительных синхронных моментов необходимо, чтобы

О                                                                                                                                                                                                                      1,0

Рис 25-10 Опытная кривая моментов асинхронного двигателя с 2р = 4, Z_x= 24, Z₂ = 28

Несколько более слабые синхронные моменты возникают также при других соотношениях между Z_% и Z_t.

Синхронные моменты могут быть уменьшены во много раз также скосом пазов ротора на зубцовое деление ротора, так как это вызывает соответствующий сдвиг по фазе в пространстве взаимодействующий гармоник поля статора и ротора вдоль оси машины,8 Наконец, величина асинхронных и синхронных моментов уменьшается при увеличении воздушного зазора.. На рис. 25-10 приведена кривая моментов асинхронного двигателя nprf наличии значительных паразитных моментов, снятая опытным путем Меллерои для асинхронного двигателя с 2р = 4, 2_Х = 24 и 2₂ = 28.

Радиальные вибрационные силы возникают в случае, когда в воздушном за-о зоре машиньГсуществуют магнитные поля, числа пар полюсов pi и р₂ которых близки друг к другу. В качестве примера на рис. 25-11, а представлены кривые индукции В₄ и В_в двух синусоидально распределенных полей с 2р = 4 и 2р = 6, а также кривая результирующего поля J3₄ + В₆. Радиальные усилия притяжения F, действующие на участки статора и ротора, пропорциональны (В₄+ В₆)² (рис. 25-11, б). Как следует из рис. 25-11,6, сумма сил притяжения на одной половине окружности значительно больше, чем на другой. Вследствие этого возникает одностороннее притяжение ротора к статору. Если поля B_i и B_s вращаются относительно друг друга, то вращаются также вибрационные силы, вызывая вибрацию ротора. Эта вибрация тем больше, чем больше слабина

в подшипниках и чем меньше жесткость вала ротора. Одновременно при недостаточной жесткости статора возникают деформация и вибрация его.

На рис. 25-11, а показан случай, когда р_х и р_г не имеют общих делителей. При этом пространственный период радиальных сил равен окружности зазора. Если же р_х и р₂ имеют общий наибольший делитель t > 1, то образуется t периодов пространственного распределения сил F (например, при 2р = 8 и 2р = 12 две следующие друг за другом кривые на рис. 25-11, б). В этом случае односто-

Рис. 25-11. Образование неуравновешенных радиальных вибрационных сил

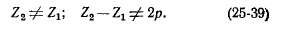
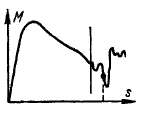
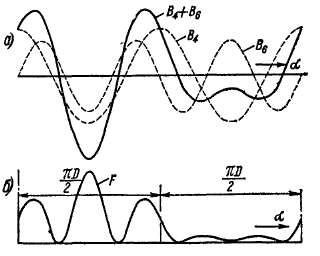
роннего притяжения ротора к статору не будет, так как силы уравновешиваются, однако возникает волнообразная деформация сердечников статора и ротора.

При пуске и работе асинхронного двигателя существует много разных гармонических полей, которые вращаются относительно друг друга и среди которых имеются поля с близкими числами пар полюсов. Однако наибольшие радиальные силы, деформации и вибрации вызываются полями с малыми числами полюсов, так как эти поля обычно наиболее сильные и распределение радиальных сил имеет при этом большой пространственный период, что вызывает увеличение деформации.

При изменении скорости вращения ротора в период пуска скорости вращения радиальных вибрационных сил и частоты вибрации также изменяются. При этом часто при некоторых значениях скорости ротора возникает явление резонанса с частотами собственных колебаний статора и ротора. Вибрация при этом становится значительной.

Вибрации, возникающие в результате действия электромагнитных сил, вызывают также шум машины. Этот шум обычно намного превосходит вентиляционный шум машины.

Электромагнитные вибрации и шум значительно снижаются при скосе пазов. Таким образом, скос пазов является эффективной мерой борьбы с вредным влиянием высших гармоник во всех его аспектах. Поэтому скос пазов иногда применяется в короткозамкнутых двигателях мощностью до 20 кет и более. Таблицы благоприятных чисел пазов статора и ротора короткозамкнутых асинхронных двигателей приводятся в руководствах по проектированию электрических машин.

§ 25-4. Гистерезисный, вихревой и реактивные моменты

Гистерезисный и вихревой моменты. Кроме рассмотренных выше вращающих моментов, возникающих вследствие взаимодействия токов в обмотке с магнитным полем, существуют моменты, вызванные явлением гистерезиса и вихревыми токами в сердечнике ротора.

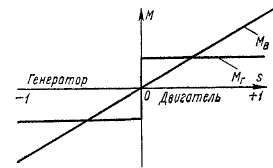
Момент от вихревых токов, или вихревой момент, М_в по своей природе совершенно аналогичен рассмотренному выше электромагнитному моменту машины, так как возникает в результате взаимодействия индуктированных в сердечнике ротора вихревых токов с магнитным- полем.

Возникновение гистерезисного момента М_г вызвано тем, что вследствие явления гистерезиса в стали сердечника ротора перемагничивание ротора магнитным полем статора совершается с некоторым запозданием по отношению к этому полю, движущемуся относительно ротора. При этом волны магнитной индукции на поверхностях статора и ротора оказываются сдвинутыми на некоторый угол <р_г, который называется углом гистерезиса и зависит от магнитных свойств материала сердечника ротора. Такой сдвиг будет существовать и при синхронном вращении ротора. В результате получается такое же взаимное расположение волн индукции или «полюсов» магнитного поля статора и ротора, какое изображено на рис. 25-8. Рис. 25-8, а соответствует двигательному режиму, когда ротор вращается медленнее поля статора и при этом возникает гистерезисный момент М_Т, действующий в сторону вращения ротора. Рис. 25-8, в соответствует генераторному режиму, когда ротор вращается быстрее поля и при этом M_t действует в противоположную сторону. При синхронной скорости вращения ротора взаимное расположение «полюсов» статора и ротора может соответствовать как положениям на рис. 25-8, айв, так и любому промежуточному положению, в частности изображенному на рис. 25-8, б, когда М_г = 0. Это зависит от направления и величины приложенного к валу машины внешнего вращающего момента или механической мощности. Таким образом, при синхронной скорости гистерезисный момент М_г может изменяться в пределах от некоторого М_тт до — М_тт,

Из сказанного следует, что гистерезисный и вихревой моменты в режимах двигателя и генератора производят полезную работу и развивают полезные

механические мощности Р_{г мх} и Р_{в мх}, как и основной электромагнитный момент машины

Рассмотрим зависимости М_г и М_в от скольжения

Потери на гистерезис в сердечнике ротора р_г2 пропорциональны частоте перемагничивания /₂ = sf_ly а потери на вихревые токи р_в2 пропорциональны /|. Поэтому при Ф = const

Prs = ^Ргао. Рва = s²Pb2o.                                  (25-40)

где Р_г20 и Р_в20 — соответствующие потери при п = 0 или s= 1.

Механические мощности Р_{г мх}, Р_{в мх} и потери р_2г, р_в2 развиваются за счет соответствующих электромагнитных мощностей Р_г. _эм и Р_{в эм}, передаваемых со

Рис 25-12 Зависимости гистерезис-

ного (М_г) и вихревого (М_в) моментов

от скольжения

Рис 25-13 Представление о возникновении реактивных моментов

статора на ротор через магнитное поле, и поэтому между ними существуют такие же соотношения, как и между Р_МХ) р_эл2 и Я_эм, рассмотренными в §24-5 Вследствие этого на основании выражений (24-78) и (25-40)

где р — число пар полюсов

На основании изложенного выше и соотношений (25-42) на рис 25-12 изображены зависимости М_г и М_в от скольжения при условии Ф = const.

В нормальных асинхронных машинах сердечники ротора изготовляются из изолированных друг от друга листов электротехнической стали, обладающей малым гистерезисом Поэтому М_т и М_в в этих машинах малы и при расчете машин не учитываются Однако действие некоторых специальных типов асинхронных и синхронных машин полностью основано на действии вихревых токов или явлений гистерезиса (см § 29-3, 41 6)

Реактивные моменты возникают в связи с тем, что на ферромагнитное тело, находящееся в магнитном поле (рис. 25-13), действуют электромагнитные силы F,

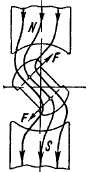
стремящиеся повернуть это тело в положение, соответствующее наименьшему магнитному сопротивлению магнитной цепи. Реактивные моменты могут возникать в электрических машинах, имеющих явновыраженные полюсы или зубчатое строение статора и ротора. В зависимости от различных обстоятельств эти моменты могут оказывать вредное влияние на работу машины или же быть использованы для получения полезного действия.

В асинхронных машинах сильные реактивные моменты возникают в случае, когда Z\ = Z₂. При этом под воздействием магнитного поля зубцы статора и ротора стремятся расположиться друг против друга.

друг друга на статор и ротор будет действовать М_г Ф 0 того или иного направления. Асинхронные двигатели с Zx~ Z₂ из-за действия таких реактивных моментов при пуске не способны сдвинуться с места (так называемое явление прилипания), а при вращении ротора возни-                                                                                                                                                                                                                                                           Ротор кают пульсирующие моменты. Рассматриваемые _{р 25}.,_{4 к обра3}о_Ванию здесь реактивные моменты при Z_x = Z₂ не еле- „ея "и „ных моментов в асин дует смешивать с рассмотренными в § 25-3 син- Р™_м ^"е с" ™ хронными моментами, так как последние возни- га                                                                                                                                                                                                             i z кают в результате взаимодействия магнитных

полей высших гармоник, созданных токами статора и ротора, в то время как реактивные моменты возникают даже при разомкнутой обмотке ротора и отсутствии в ней тока. Следует отметить, что результирующий реактивный момент при Z_x = Z₂ можно свести к нулю путем скоса пазов.

В нормальных асинхронных машинах Z^ и Z₂ представляют собой достаточно большие не равные и не кратные друг другу числа. Поэтому отдельные зубцы ротора занимают различные положения относительно зубцов статора и суммарный реактивный момент равен или близок нулю. В связи с этим в нормальных асинхронных машинах реактивные моменты не учитываются. Однако действие некоторых специальных типов электрических машин полностью основано на действии реактивных моментов (см. § 25-3, 41-4).

---

Содержание
Предыдущий § Следующий