Содержание
Предыдущий § Следующий

Глава двадцать третья МАГНИТНЫЕ ПОЛЯ И ИНДУКТИВНЫЕ СОПРОТИВЛЕНИЯ ОБМОТОК ПЕРЕМЕННОГО ТОКА

§ 21-1 Магнитные поля обмоток переменного тока

Общая характеристика магнитного поля обмотки. Магнитное поле* создаваемое током обмотки, подразделяется на три пространственные зоны: 1) поле воздушного зазора, 2) поле пазов и 3) поде лобовых частей обмотки.

Магнитные линии поля воздушного зазора пересекают воздушный зазор и замыкаются через сердечники статора и ротора. Это

поле создается рассмотренной главе намагни-силой обмотки. Магнитное поле пазов (рис. 23-1) создается токами проводников паза, и к нему относятся линии магнитной индукции, которые не пересекают воздушного зазора и замыкаются в пределах данной части машины. Магнитное поле лобовых частей обмотки (рис. 23-2) сосредоточено в области лобовых пространств обмотки.

В действительности существует единое магнитное поле обмотки, однако, пользуясь принципом наложения, можно рассматривать перечисленные выше поля по

отдельности. В частности, можно рассматривать отдельно поле тока каждого паза (см. рис. 23-1), хотя поля токов всех пазов складываются в общее поле более сложного характера.

Все магнитные линии поля зазора замыкаются через сердечники машины. Большая часть магнитных линий полей пазов и часть магнитных линий полей лобовых частей также замыкаются через сердечник. Однако эти поля, а также высшие гармоники поля зазора в нормальных режимах работы машины малы по сравнению с основной гармоникой поля зазора, и стегГень насыщения сердечников статора и ротора определяется практически магнитным потоком этой основной гармоники.

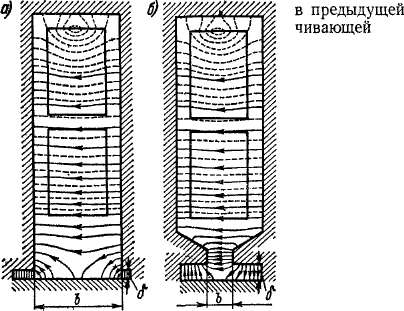Рис. 23-1. Магнитные поля пазов

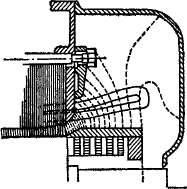Рис 23-2 Магнитное поле в лобовом пространстве турбогенератора

Полезное действие машины переменного тока, за редким исключением некоторых машин специального назначения, основано на действии магнитного поля основной гармоники воздушного зазора. Это поле поэтому является главным, или рабочим,

а поля пазов и лобовых частей — полями рассеяния. К последним относятся также поля высших гармоник воздушного зазора, которые называются полями рассеяния воздушного зазора или полями дифференциального рассеяния.

Второе название обусловлено тем, что эти поля представляют собой разность между полным полем воздушного зазора и его основной гармоникой.

Таким образом, магнитное поле рассеяния состоит из трех главных частей: 1) пазового, 2) лобового и 3) поля рассеяния воздушного зазора, или дифференциального.

Ниже в данном параграфе более подробно рассматривается поле воздушного зазора при симметричной нагрузке обмотки. При этом имеется в виду неявнополюсная машина.

Поле воздушного зазора при отсутствии зубчатости якоря и насыщения определяется при допущениях, перечисленных в начале § 22-1. При этих условиях пазов на поверхностях статора и ротора нет, воздушный зазор является равномерным по всей окружности и, следовательно, искажающее влияние пазов и насыщения магнитной цепи на распределение поля в зазоре отсутствует. Поэтому каждая гармоника н. с. создает только гармонику магнитного поля такого же порядка v. Амплитуда магнитной индукции этой гармоники B_mv вычисляется по формуле (22-5) как произведение магнитной проводимости зазора Л_б на амплитуду гармоники н. с. F_v. Учитывая выражения (22-3) и (22-31), для случая симметричной нагрузки m-фазной обмотки получим

При наличии пазов поле в зазоре искажается. В этом случае в магнитных потоках основной и высших гармоник поля воздушного зазора, создаваемых вычисленными в гл. 22 -намагничивающими силами обмоток, будем учитывать только те линии магнитной индукции, которые достигают противоположной стороны воздушного зазора, т. е. пересекают зазор от статора к ротору и наоборот (см. рис. 23-1).

Магнитная индукция поля, создаваемого основной гармоникой н. с. обмотки, уложенной в пазах, имеет на противоположной, гладкой стороне воздушного зазора распределение вида кривой 1 на рис.'23-З, а. Такая кривая содержит наряду с основной гармоникой (кривая 2) целый ряд высших гармоник. С вполне достаточной для большинства практических целей точностью можно считать, что

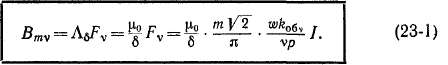
амплитуда основной гармоники поля при этом уменьшаете^ (см. рис. 23-3, а) в

раз, где k& — коэффициент воздушного зазора (см. § 2-2). Поэтому вместо выражения (22-3) следует писать

При наличии пазов также и на противоположной стороне зазора и радиальных вентиляционных каналов значение Лв нужно рассчи*

тывать с учетом всех этих неравномерно-* стей зазора. При этом определяется средней; по активной длине машины значение В_ть В действительности ц_с Ф оо и наеы« щение магнитной цепи приводит к умень> шению индукции в зазоре и к упрощению формы кривой (кривая ) на рис. 23-3, б), поскольку в области больших - индукций насыщение сказывается сильнее. Кривая (рис. 23-3, б) содержит поэтому как основ ную (кривая 2), так и высшие гармоники. Из высших гармоник наибольшее значений имеет третья гармоника (кривая 5), которая вращается синхронно с основной гармоникой и индуктирует в обмотке э. д. с. тройной частоты. Уплощение кривой индукции в большей мере проявляется в ма<< шинах с относительно малым зазором, как, например, в асинхронных машинах, и в этих, случаях учитывается при расчете магнит* ной цепи.

Степень насыщения магнитной цепи определяется видом магнитной характеристики Ф = / {F) и расположением на ней рабочей точки. Магнитная характеристика машин переменного тока рассчитывается так же, как и для машин постоянного тока, и определяется также экспе-риментально на основе характеристики холостого хода U — f (F) или U = / (/₀).

С достаточной точностью можно считать, что основная гармоника поля под влиянием насыщения уменьшается в ftp, раз (см. § 2-5). Поэтому вместо выражения (23-2) имеем

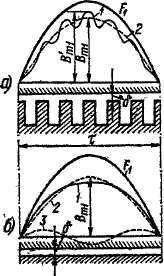Рис. 23-3. Распределение Munurraotиндукции воля, создаваемого ^f основной гармоникой н. с. при наличии пазов (а) и насыщения (б)

Величину

можно назвать эквивалентным воздушным зазором.

При наличии зубчатости якоря каждая высшая гармоника н. с. v создает, кроме гармоники v, ряд других гармоник поля. В первом приближении можно считать, что каждая гармоника н. с. создает юлько поле гармоники такого же порядка, и поэтому к этим гармоникам также применимо соотношение (23-3). При этих условиях как для основной, так и для высших гармоник поля вместо выражения (23-1) получим

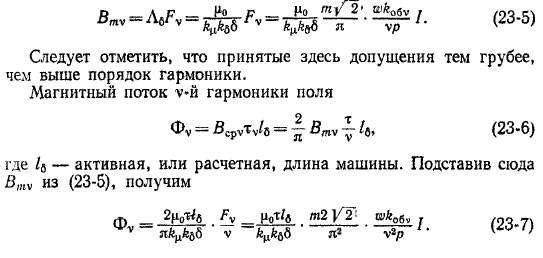§ 23-2. Главные индуктивные сопротивления обмоток переменного тока

Общие положения. Ниже будем иметь в виду машины неявно-полюсной конструкции, в частности асинхронные машины. Особенности, возникающие в явнополюсных машинах, будут рассмотрены в гл. 32.

Вращающиеся гармоники магнитного поля обмотки статора асинхронной машины, перемещаясь относительно этой обмотки, индуктируют в ней э. д. с. самоиндукции, частота которых при равномерном воздушном зазоре равна частоте тока в данной обмотке. Одинаковость частот этих э. д. с. гармоник поля объясняется тем, что, хотя гармоника порядка v вращается в v раз медленнее основной, она имеет в v раз больше полюсов. Можно доказать, что все эти э. д. с. совпадают по фазе. Сказанное относится также к э. д. с. самоиндукции, индуктируемым гармониками поля ротора в самой обмотке ротора.

При неподвижном роторе частоты всех э. д. с. взаимной индукции, индуктируемых гармониками поля статора в обмотке ротора и наоборот, т. е. гармониками поля ротора в обмотке статора, также одинаковы и равны основной частоте. Однако при вращающемся роторе частоты э. д. с. взаимной индукции от различных гармоник поля различны, так как в этом случае скорости вращения гармоник статора относительно ротора и наоборот, т. е. гармоник ротора относительно статора, уже не обратно пропорциональны числам их полюсов. Поэтому во вращающейся машине высшие гармоники поля не создают э. д. с. взаимной индукции основной частоты и их следует, отнести к полям рассеяния. Эффекты, которые могут вызвать токи, создаваемые э. д. с. взаимной индукции от высших гармоник поля, имеют в общем случае второстепенный характер, и их необходимо рассматривать отдельно. Ввиду наличия пазов на статоре и роторе при вращении ротора возникают также дополнительные гармоники, поля, которые индуктируют в обмотках э. д. с. различных, в том числе и относительно высоких, частот. При нормальной конструкции машины эти э. д. с. не имеют существенного значения и ниже не рассматриваются.

В теории электрических машин переменного тока, как и в других областях электротехники, э. д. с. переменного тока Е, которые индуктируются магнитными полями, созданными переменными токами /, учитываются с помощью индуктивных сопротивлений

В электрической машине переменного тока при этом каждой гармонике поля v соответствуют определенные значения индуктивных сопротивлений само- и взаимной индукции x_v.

Работа машин переменного тока основана на действии основных гармоник поля.

I Индуктивные сопротивления, соответствующие этим гармоникам, назовем главными.

Определим величины главных индуктивных сопротивлений, опуская при этом индексы, указывающие на порядок гармоники. Величины, относящиеся к статору и ротору, обозначим соответственно индексами 1 и 2.

Выражения для главных индуктивных сопротивлений. Э. д. с. самоиндукции Е_г, индуктируемую в обмотке статора потоком основной гармоники Ф_1; найдем, если подставим в (20-19) значение потока Ф = Ф_х из (23-7), полагая при этом v = 1 и обозначая величины, относящиеся к статору, индексами 1. Тогда получим

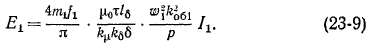
Главное собственное индуктивное сопротивление обмотки статора, согласно выражениям (23-8) и (23-9),

Далее будем полагать /₂ = f_lt что в асинхронной машине соответствует неподвижному ротору. В противном случае в соответствующих выражениях достаточно заменить f₁ на /₂. Тогда аналогичным образом для главного собственного индуктивного сопротивления обмотки ротора получим

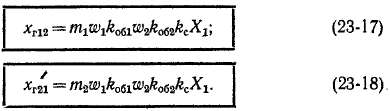
Э. д. с. взаимной индукции £₁₂, индуктируемую основной гармоникой поля статора в обмотке ротора, найдем аналогично Е_х по (23-9), если в (20-19) будем писать индексы ротора 2, а в (23-7) — индексы статора 1. Э. д. с. взаимной индукции Е₂ъ индуктируемую основной гармоникой поля ротора в обмотке статора, определим подобным же образом, однако в (20-19) нужно писать индексы статора, а в (23-7) — индексы ротора. При этом

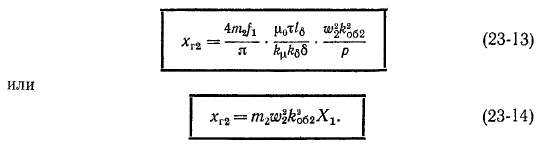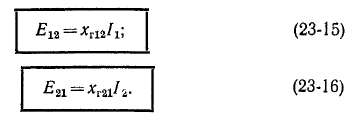
460                                                                                                                                                                                                                         Общие вопросы теории машин переменного тока [Разд. Ill

и для главных взаимных индуктивных сопротивлений получим выражения:

По выражениям (23-17) и (23-18) дг_г12 ф х_г21, что объясняется тем, что эти сопротивления являются эквивалентными и учитывают действие поля всех фаз одной обмотки на другую. Например, x_Tt2 учитывает э. д. с, индуктированную полем всех tn_x фаз первичной обмотки в фазе вторичной обмотки. В выражения (23-17) и (23-18) введены коэффициенты скоса k_c для основной гармоники поля [см. равенство (20-3)1, так как при наличии скоса пазов на одной из частей машины магнитное поле другой части машины будет скошено относительно проводников первой части машины, что вызовет уменьшение индуктированной э. д. с. В то же время в соотношения (23-10), (23-11), (23-13) й (23-14) этот коэффициент не входит, так как поле данной обмотки ориентировано всегда в направлении ее пазов и проводников. При отсутствии скоса в формулах (23-17) и (23-18), естественно, надо положить &_с = 1.

Как и всякие индуктивные сопротивления, x_tl, х_п, х_гП и а:_г21: пропорциональны частоте тока и квадрату чисел витков или произведению чисел витков двух обмоток, а также обратно пропорциональны величине эквивалентного воздушного зазора.

При пользовании полученными выражениями необходимо подставлять такое значение k^, которое соответствует насыщению машины в рассматриваемом режиме работы.

Относительная величина главного собственного индуктивного сопротивления. Номинальное сопротивление z_H выражается через номинальные фазные напряжения и ток:

Пусть Вьн означает амплитуду индукции основной гармоники поля воздушного зазора при условии, что основная гармоника э. д. с, обмотки статора E_t = U_s. Тогда на основании выражений (20-19) и (23-6) при v = 1

Полагая в равенстве (22-33) А = А_я и / = /_н, выразим с помощью этого равенства номинальный ток статора /_и через номинальную линейную нагрузку статора А_в:

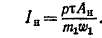
Так как величины А_п и Ва„ определяются главным образбм условиями охлаждения и качеством магнитных материалов, то в машинах данной конструкции они изменяются в сравнительно узких пределах. Поэтому величина дг_г1* зависит главным образом от отношения т/б. Для машины заданной мощности и скорости вращения х_кЫ зависит в основном от величины зазора б. В синхронных машинах относительная величина зазора всегда больше, чем в асинхронных, и поэтому у первых х_г1* всегда меньше, чем у вторых.

Из выражения (23-23) следует также, что в крупных турбогенераторах с внутренним охлаждением проводников обмоток, у которых Л_н достигает весьма больших значений, для ограничения величины л:_г1* нужно существенным образом увеличивать б.

В практике заводских расчетов относительные значения сопротивлений иногда выражают через величины потока Ф_н при Е = (/„ и н. с. якоря F_H при / = /_н. Такие выражения нетрудно получить, используя соотношения (20-9), (20-19) и (22-31), Для х_т1% вместо (23-23) при этом получим

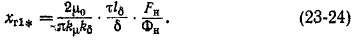
§ 23-3. Индуктивные сопротивления рассеяния обмоток переменного тока

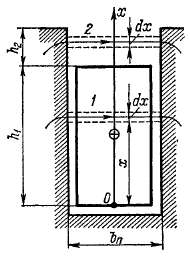
Краткая характеристика полей рассеяния была дана в § 23-1. Произведем здесь расчет индуктивных сопротивлений рассеяния. Пазовое рассеяние. Рассмотрим паз простейшей конфигурации с одной катушечной стороной в пазу (рис. 23-4) и предположим дли простоты, что линии магнитной индукции поля рассеяния паза пересекают паз прямолинейно, перпендикулярно его боковым стенкам. Такое предположение не слишком сильно отличается от действительности (см. рис. 23-1), и необходимые коррективы могут быть внесены отдельно. Вычислим потокосцепление проводников паза (w_K) с потоком, создаваемым током катушки i_K.

В нижней части паза высотой h_lt занятой катушкой (зона /), линия магнитной индукции В_х1 на высоте х создается током

Z- w_Ki_K и сцепляется с числом витков Д- w_K. «1                                                                               "1

Полагая для стали ц_с = оо по закону

полного тока имеем

Рис. 23-4. Поле рассеяния паза

В верхней части паза высотой h₂ (зона 2) индукция B_xi определяется полным током паза:

Можно принять приближенно, что поле рассеяния катушек в радиальных вентиляционных каналах в два раза слабее, чем в пазах. При этом расчетная длина поля рассеяния

где п_вент и Ь_вент — число и ширина вентиляционных каналов: 1_С — полная длина сердечника вместе с вентиляционными каналами. Сечения элементарных трубок магнитного потока высотой dx (рис. 23-4) составляют 1'₆ dx. Потоки этих трубок

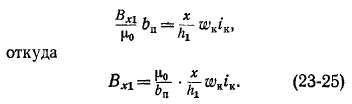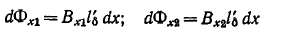
называется относительной магнитной проводимостью рассеяния паза и определяет потокосцепление рассеяния паза на единицу длины машины.

Параллельная ветвь однослойной обмотки имеет 2pq/a катушечных сторон и число витков, равное

Равенство (23-33) пригодно также для двухслойных обмоток и для пазов иной формы. Выражения для К_П при других формах пазов находятся аналогично, при тех же предположениях о характере поля рассеяния паза. В двухслойных обмотках с укороченным шагом в части пазов находятся катушечные стороны разных фаз, и поля рассеяния этих пазов будут слабее. При этом в выражение для %_а войдет также относительная величина шага. Формулы для К_а при различных формах пазов, также с учетом укорочения шага приводятся в руководствах по проектированию электрических машин,

Из выражения (23-30) следует, что пазовое рассеяние тем больше, чем выше и уже пазы. Обычно к_а =1,0-5- 4,0.

Рассеяние по коронкам зубцов. Принятое выше допущение о виде магнитных линий рассеяния паза заметно нарушается вблизи воздушного зазора (см. рис. 23-1). Вследствие этого при больших значениях ЫЬ (см. рис. 23-1, а) в связи с ослаблением поля паза вблизи зазора рассеяние уменьшается. При малых ЫЬ (см. рис. 23-1, 6) необходимо учесть магнитные линии, замыкающиеся вокруг паза от одного зубца к другому, но не доходящие до противоположной стороны зазора, и в результате рассеяние увеличивается. Эффект изменения рассеяния паза вследствие указанных явлений учтем в виде добавочной составляющей рассеяния, которую назовем рассеянием по коронкам зубцов. Для индуктивного сопротивления рассеяния по коронкам зубцов х_к можно получить формулу вида (23-33), с заменой Х„ на магнитную проводимость рассеяния по коронкам зубцов %_к. Формулу для К_к можно вывести, используя для анализа поля в рассматриваемой области соотношения, получаемые методом конформных отображений. Формула для %_к приобретает вид¹

где b — величина открытия паза.

Зависимость К_к = / (6/6) приведена на рис. 23-5. При больших воздушных зазорах рассеяние по коронкам зубцов составляет

¹ A. Ifc Вольдек. Рассеяние по коронкам зубцов в электрических машинах. — «Вестник электропромышленности», 1961, № 1, с. 60—62.

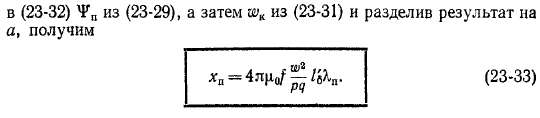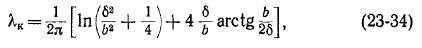
значительную положительную величину. Наоборот, при малых б рассеяние по коронкам зубцов отрицательно. При укороченном шаге А,_к нужно множить на такой же коэффициент, как и проводимость для верхней части паза.

Лобовое рассеяние. Основная и высшие гармоники пространственного распределения токов лобовых частей обмотки создают вращающиеся поля, как и в активной части машины. Однако ввиду сложной формы лобовых частей, а также по ряду других причин поле лобовых частей имеет весьма сложную структуру и не является плоскопараллельным. Главное значение имеет основная гармоника поля.

Поля лобовых частей статора сцепляются с лобовыми частями ротора и наоборрт. Поэтому эти поля индуктируют как э. д. с. самоиндукции так и э, д. с. взаимной индукции. Э.д. с. взаимной индукции лобовых частей по сравнению с э. д. с, взаимной индукции активной части машины малы и большей частью лежат в пределах „точности расчета последних. Поэтому при расчете э.д. с, всей обмотки э.д. с. взаимной индукции лобовых частей статора и ротора можно пренебречь. Однако ввиду наличия взаимной индукции поля лобовых частей нельзя относить полностью к

рассеянию и при расчете индуктивных сопротивлений рассеяния явление взаимной индукции должно быть принято во внимание.

Аналитическое исследование полей и индуктивных сопротивлений рассеяния лобовых частей при некоторых упрощающих предположениях можно выполнить с помощью методов теории электромагнитного поля. Однако получаемые при этом соотношения весьма сложны и малопригодны для повседневных инженерных расчетов. Поэтому на практике пользуются формулами эмпирического характера.

Формулам для индуктивного сопротивления рассеяния лобовых частей х_л во всех случаях можно придать вид, аналогичный равенству (23-33), с заменой Я,_п на магнитную проводимость лобового рассеяния Я_л. Для двухслойных обмоток многополюсных машин применяется формула

Рис 23-5. Магнитная проводимость рассеяния тю коронкам зубцов

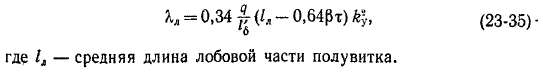
Формулы аналогичного характера для других видов обмоток приводятся в пособиях по проектированию электрических машин.

Дифференциальное рассеяние. Допустим сначала, что наличие пазов сказывается в том, что амплитуды индукции всех гармоник поля уменьшаются в k₈ раз [см. равенство (23-5)]. Тогда сопротивления самоиндукции всех гармоник поля выражаются равенством (23-10), если заменить в нем k_o6 на k_o6v и разделить результат на v², так как поток Ф_у гармоники v, согласно (23-7), обратно пропорционален V².

Индуктивное сопротивление дифференциального рассеяния обмотки х_д равно сумме сопротивлений самоиндукции всех гармоник, за исключением гармоники v = 1. Поэтому на основании выражения (23-10)

Отношение х_я к главному индуктивному сопротивлению обмотки называется коэффициентом дифференциального рассеяния k_A. На основании выражений (23-36) и (23-10)

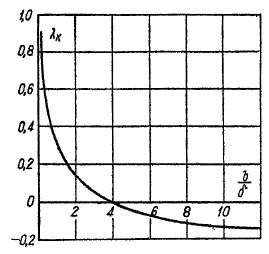
Значения k_A можно вычислить по формуле (23-37), введя в расчет достаточное число гармоник. Для разных типов обмоток получены также формулы для &_д в конечном виде. Зависимость £_д от относительного шага Р для двухслойной обмотки с фазной зоной а = 60° при разных q представлена на рис. 23-6.

Для беличьей клетки fe^j = kl^ = 1, и в этом случае, согласно выражениям (22-42), (22-43) и (23-37), получим

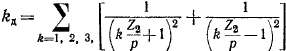Ряд в этом равенстве может быть суммирован в конечном виде, и при этом выражение к_д для беличьей клетки будет

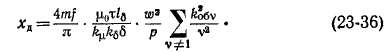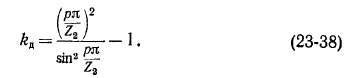
По известным значениям k_K величины х_А могут быть вычислены по формуле

Хотя И_я мало (см. рис. 23-6), в машинах с относительно малым воздушным зазором сопротивление х_л по сравнению с другими составляющими сопротивления рассеяния достаточно велико, так как лг_г по сравнению с ними велико.

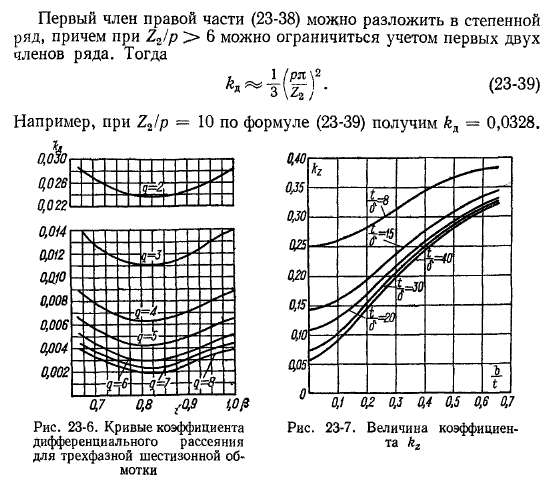
При более тщательном рассмотрении вопроса выясняется, что под влиянием пазов сопротивление х_л уменьшается на заметную величину. Для фазных обмоток с целым q и для беличьей клетки коэффициент &_д [см. равенство (23-37)] необходимо уменьшить на величину

где величина к_г определяется по графику рис. 23-7 (t — зубцовый шаг).

Необходимо иметь в виду, что высшие гармоники поля статора! индуктируют з, д. с. в обмотке ротора, а также в теле ротора, если? оно является массивным. Вызванные этими э. д. с. токи создают! свои магнитныеполя, которые ослабляют, или частично демпфируют* поля высших гармоник статора. В результате "сопротивление л» обмотки статора уменьшается. Ё случае если на роторе имеется фаз* ная обмотка и его сердечник шихтован (например, асинхронны^ двигатели с фазным ротором), демпфирование весьма незначительно; и формулы с поправкой Д&_д являются достаточно строгими. Наобо-^! рот, когда на роторе имеется беличья клетка, а также когда ротор или его полюсы массивные, демпфирование заметно, так как дли токов, вызываемых высшими гармониками, образуются контур^ с малым сопротивлением. Демпфирование может быть учтена уменьшением величины k_A посредством введения в качестве сомно* жителя соответствующего коэффициента демпфирования k_m < 1,

Формуле для х_д можно придать также вид формулы (23-33) путем замены К_а на соответствующую величину К_л, которая называете? магнитной проводимостью дифференци а ль ного рассеяния. При этом

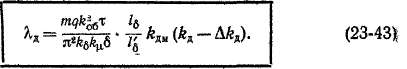Подставив сюда х_Д из (23-40) и затем х_г1 из (23-10), а также учитывая указанные поправки, получим

В практике заводских расчетов Я_д определяют обычно по раа? личным приближенным формулам.

Рассеяние скоса. При скосе пазов или полюсов статора и ротора относительно друг друга рассеяние увеличивается, так как э. д. ci и индуктивные сопротивления самоиндукции от основной гармоники поля при этом не изменяются, а э. д. с. и сопротивления взаимной" индукции уменьшаются. В этом случае рассеяние возникает за счет основной гармоники поля машины.

Определение рассеяния скоса связано с основами теории электрических машин и производится поэтому ниже (см. § 24-3). Выражению для индуктивного сопротивления рассеяния скоса х_с также можно придать вид формулы (23-33) яутем замены К определенной величиной Ji_c, которую можно назвать магнитной проводимостью рассеяния скоса.

Полное индуктивное сопротивление рассеяния обмотки х„ определяется путем суммирования всех перечисленных частичных сопротивлений рассеяния:

или

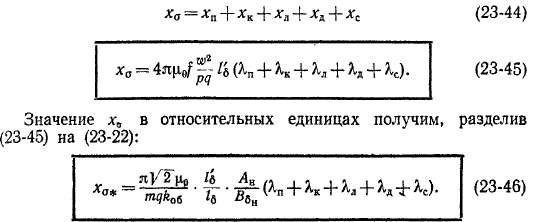В асинхронных машинах главные составляющие рассеяния: пазовое, лобовое и дифференциальное — имеют примерно одинаковый удельный вес. При наличии скоса пазов существенное значение приобретает также рассеяние скоса. В синхронных машинах вследствие большой величины зазора дифференциальное рассеяние меньше пазового и лобового. В турбогенераторах ввиду большого значения q [см. выражение (15-22)] дифференциальное рассеяние очень мало. Лобовое рассеяние от величины q практически не зависит, так как Х._л 1см. выражение (23-35)] пропорционально q и, кроме того, q входит в знаменатель формул (23-45) и (23-46). Величина Я_п также пропорциональна q, так как величина Ь_п в (23-30) при данном т обратно пропорциональна q. Поэтому пазовое рассеяние также практически не зависит от q.

В машинах с воздушным охлаждением обычно х_а* ~ 0,08 -*■ 0,15. Как видно из (23-46), при увеличении Л_н, что связано с интенсификацией способов охлаждения, величина х_ащ. возрастает. В турбогенераторах с внутренним охлаждением обмоток х_а% — 0,20 -f- 0,35.

В пределах до / « 1,5//_н сопротивление х_а практически постоянно, так" как магнитные потоки рассеяния замыкаются по воздуху и поэтому мало зависят от насыщения. Однако при больших токах (например, при коротких замыканиях синхронных генераторов и пуске асинхронных двигателей) потоки рассеяния сильно возрастают и вызывают насыщение зубцовой зоны. При этом Xf, уменьшается на 15—30%.

Сопротивление рассеяния х_а представляет собой часть полного собственного индуктивного сопротивления обмотки х. Второй, притом наибольшей составляющей этого сопротивления является главное индуктивное сопротивление обмотки х^, обусловленное основной гармоникой поля в зазоре (см. § 23-2).

§ 23-4. Расчет магнитного поля в воздушном зазоре с учетом его равномерности методом удельной магнитной проводимости зазора

Предварительные замечания. Наличие пазов на поверхностях статора и ротора электрических машин вызывает сильное искажение магнитного роля в зазоре и появление зубцовых пространственных гармоник этого поля. Эти гармоники вызывают добавочные потери в стали и в короткозамкнутых обмотках, искажение кривой вращающего момента (см. § 25-3), изменение индуктивных сопротивлений дифференциального рассеяния (см. § 23-3) и появление шума в машине. В то же время полезное действие некоторых специальных видов электрических машин малой мощности основано на указанных зубцовых гармониках поля (см. § 41-4 и 41-5). В явнополюсных синхронных машинах неравномерность зазора обусловлена также наличием явновыраженных полюсов и междуполюсных пространств между ними, которые аналогичны зубцам и пазам, сильно влияют на структуру поля в зазоре и тем самым оказывают большое влияние на рабочие свойства машины.

Все эти обстоятельства вызывают необходимость достаточно глубокого изучения влияния неравномерности зазора на магнитное поле. Ввиду слож-ной структуры магнитного поля в зазоре при зубчатом якоре этот вопрос трудно поддается исследованию. С достаточной для инженерных целей точностью поле в зазоре может быть исследовано по методу удельной магнитной проводимости зазора.

Магнитное поле в зазоре при односторонней зубчатости. Рассмотрим здесь неявнополюсную машину, например асинхронную, у которой пазы имеются только на одном сердечнике, например на сердечнике статора. Предположим также, что для стали \и,_с = со. Исследуем сначала магнитное поле, которое возникает в зазоре такой машины в случае, когда на каждом двойном полюсном делении расположена катушка с полным шагом (у = т) и полным током w_Ki (рис. 23-8, а). Распределение магнитной индукции В поля таких катушек на поверхности гладкого сердечника представлено в виде зубчатой кривой / на рис. 23-8, б. Прямоугольная волна н. с. F указанного ряда катушек изображена в виде кривой 1 на рис. 23-8, в.

В § 22-1 для случая равномерного зазора связь между В и F была установлена в виде соотношения

была названа удельной магнитной проводимостью зазора. Распространим соотношение (23-47) также на случай неравномерного зазора, определив для этого соответствующим образом величину Л_а.

Допустим сначала, что в области пазов, занятых катушечными сторонами, индукция В изменяется по такому же закону (кривая 2 на рис 23-8, б), как и в области пазов, где катушечных сторон нет (кривая 1 на рис. 23-8, б), и разделим ординаты кривой 2 рис. 23-8, б на ординаты кривой / рис. 23-8, в. Тогда получим волнистую кривую с периодом, равным зубцовому делению, изображенному на рис. 23-8, г. В соответствии с равенством (23-47) эта кривая представляет собой удельную проводимость зазора Ад при односторонней зубчатости. Однако теперь при пользовании равенством (23-47), подставив в него значения н. с. F по кривой / рис. 23-8, в и значения Ag по кривой рис. 23-8, г, получим не вполне точные значения В для области пазов занятых катушечными сторонами. Чтобы избежать этого, необходимо изменить форму кривой н. с. катушки для областей пазов с катушечными сторонами. Для этого в области этих пазов ординаты кривой /

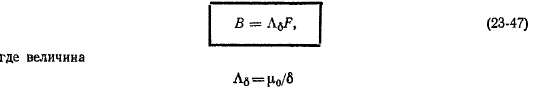
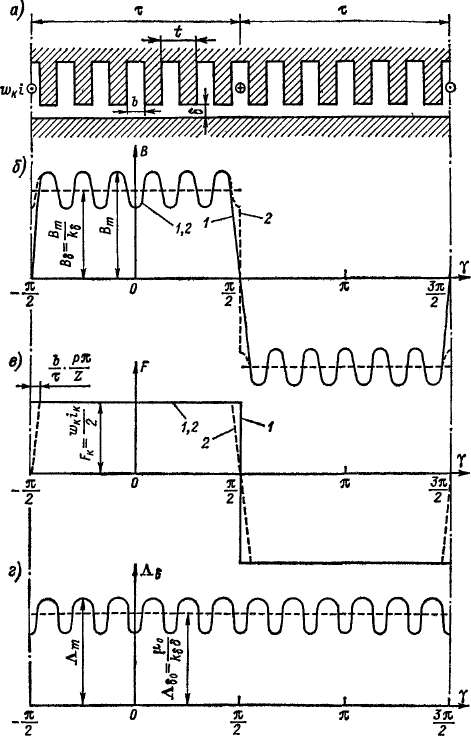Рис. 23-8. Определение удельной магнитной проводимости зазора неявнополюснои машины при односторонней зубчатости

рис. 23-8, в нужно умножить на отношение ординат кривых 1 к 2 рис. 23-8, в. Это отношение представляет собой сложную математическую функцию. Достаточно точные для практических целей результаты получаются, если принять, что на протяжении указанных пазов н. с. катушки изменяется линейно, в результате чего вместо прямоугольной кривой 1 рис 23-8, в получим трапецеидальную кривую 2, изображенную на этом же рисунке.

Если трапецеидальную кривую 2 рис. 23-8, в разложить в ряд Фурье подобно^ тому, как это было сделано для прямоугольной волны н. с. рис 22-1, то в выражение для амплитуды н с. v-й гармоники, определяемой равенством (22-7), войдет дополнительный множитель

который назовем обмоточным коэ фф иц центом открытия паза.

В формуле (23-48) t означает зубцовое деление, Ь — величину открытия паза и Z — число пазов.

Двухслойную обмотку с целым q и укороченным шагом можно представить себе состоящей из катушек с полным шагом. Поэтому, пользуясь принципом наложения, можно прийти к выводу, что формулу (23-47) можно применять и для расчета поЛя всей двухслойной, а также и однослойной обмотки, если под F понимать л. с. всей обмотки как функцию координаты, отсчитываемой по окружности, а под Лб — определяемую указанным выше образом функцию в виде кривой на, рис. 23-8, г. При этом в выражения для гармоник н. с, приведенных в гл. 22, необходимо только наряду с коэффициентами укорочения и распределения обмотки ввести в качестве множителя также коэффициент fej_v по (23-48). При этом полный обмоточный коэффициент

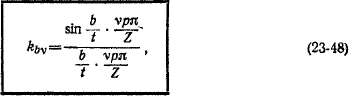Нетрудно убедиться а том, что указанным образом можно рассчитывать также поле дробных обмоток и обмоток в виде беличьей клетки.

Зависимость Ац = /(а) можно определить путем^ расчета поля в зазоре мето«-дами математической физики. Хотя при расчете поля по (23-47) можно пользоваться интегральными величинами Лд и F, во многих случаях целесообразно эти величины выражать в виде ряда Фурье.

Величину Ag по рис. 23-8, г можно выразить в виде ряда

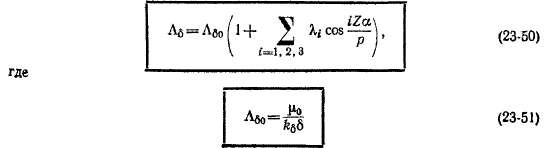
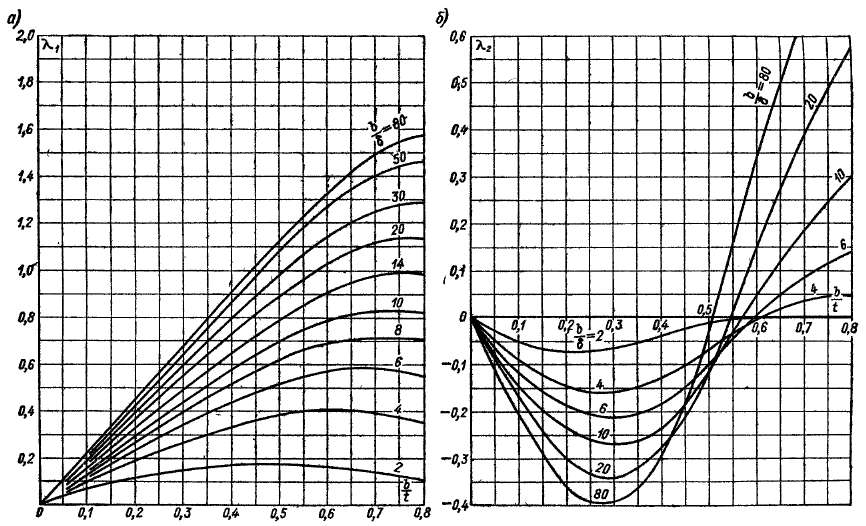Рис. 23-9. Зависимость первой (а) и второй (б) гармоник удельной магнитной проводимости зазора от геометрических

размеров зубцовой зоны

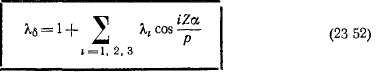представляет собой постоянную составляющую удельной проводимости зазора,

— относительную удельную проводимость зазора, а Я, — относительные величины гармоник проводимости, являющиеся функциями геометрических соотношений зубцовой зоны.

На рис 23 9 приведены графики Х_х и к₂ ^со знаками, действительными для случая, когда начало координаты а совпадает с центром зуба Если же начало

координаты а совпадает с центром паза, то знак Х_х нужно изменить на обратный

Изложенным способом магнитное поле при односторонней зубиа-тости якоря рассчитывается в принципе весьма точно.

Магнитное поле в зазоре при двусторонней зубчатости якоря является значительно более сложным, и для получения простых расчетных зависимостей необходимо пользоваться приближенными зависимостями. Анализ этого вопроса показывает, что' удовлетворительную для большинства целей точность можно получить, если положить, что в этом случае

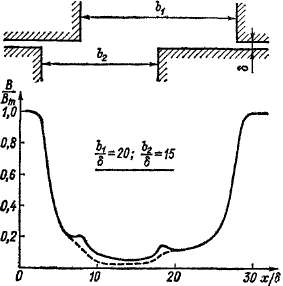Рис 23-10 Кривые удельной магнитной проводимости зазора нейвнополюсной машины при двусторонней зубчатости

где Х(ц и Ява — относительные удельные проводимости статора и ротора, причем каждая из них

рассчитана в предположении, что противоположная сторона зазора лишена пазов. Допускаемая при этом погрешность иллюстрируется кривыми рис. 23-10, где сплошная кривая представляет собой действительные значения В посередине зазора, а штриховая кривая — значения В, рассчитанные с использованием соотношения (23-53). Как видно из рисунка, расхождение этих кривых невелико.

Для Лб₀ ^в рассматриваемом случае также действительно выражение (23-51), где &а — общий коэффициент зазора, а Х^ и Xg₂ определяются равенствами вида (23-52), причем при пользовании графиками рис. 23-10 каждый раз учитываются геометрические соотношения на данной стороне зазора. В общем случае надо учитывать, что если начало координат совместить с одной из осей симметрии зубцовой зоны с одной стороны зазора, то эта ось может не совпадать с осью симметрии зубцовой зоны с другой стороны зазора.

Пусть в начальный момент времени t = 0 оси зубцов статора и ротора в начале координаты а = 0 совпадают и ротор вращается с электрической угловой скоростью

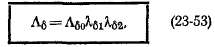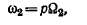
где Ог — механическая угловая скорость вращения ротора. Тогда относительные проводимости статора и ротора определяются выражениями:

Общая относительная удельная проводимость зазора на осноэании (23-54)

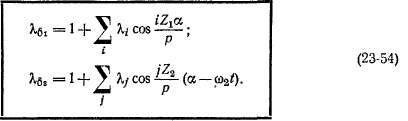Первый член правой части этого выражения определяет проводимость эквивалентного равномерного зазора б' = k(,6, второй член — гармоники проводимости статора, третий член — гармоники проводимости ротора и последний член — интерференционные гармоники проводимости, обусловленные взаимным влиянием пазов статора и ротора.

При умножении Лв по (23-53) и (23-55) на н. с. машины, выражаемую также рядом Фурье, получим бесконечные ряды разнообразных гармоник поля, с разными полюсными делениями и с разными скоростями вращения. Наибольшее влияние на работу машины оказывают лишь некоторые из них, наиболее сильные гармоники.

476                                                                                                                                                                                                                    Общие вопросы теории машин переменного тока [Разд. III

при этом, согласно {23-56) и (23-57), после замены произведения косинусов по известной тригонометрической формуле и подстановки ©а = (1 — s)a>i определяется соотношением

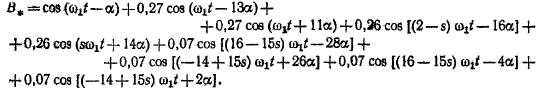Здесь каждая строка соответствует определенному члену равенства (23-56) в той же последовательности. Множитель переда определяет порядок гармоники относительно основной, а отношение коэффициента перед t к этому множителю опре* деляет скорость вращения гармоники. Последние две гармоники имеют малые числа полюсов и вращаются с большими скоростями:

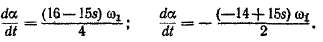Поэтому, несмотря на относительную малость амплитуд этих гармоник, они могут оказывать существенное влияние на работу машины.

Аналогичным образом можно исследовать влияние явнопс&юсной конструкции синхронной машины на ее магнитное поле. При этом можно исследовать такнк влияние низших гармоник н. с, создаваемых дробными обмотками, и свойства, синхронных машин с переключением числа полюсов.

Более подробно метод удельной магнитной проводимости рассмотрен в ряде* журнальных статей¹.

¹ Статьи А. И. Вольдека в журналах; «Электричество*, 1951, М12, с ^-^ «Труды Ленинградского политехйиче»ого^-института», 1953, №8, е. ЩуЩ «Труда Ленинградского политехнического института», 1969, № 301,_;£. 4СЦ-44 (совтяар Н. А. Солдатенкова); «ИзвестВД ъУзов- ЭпектромеханШЕ», 1964, ж % с. 638-^41', там же, 1968, № 6, с. 609—6& &6awop Р, А. Лахгметс); «Зяйктря-честада, 1966, № 7, с. 46-52; «Элек?рв*Й$«ка*, 1969, № 9, С 3-5 фоавтор Р. А. Лахт»етс).

Содержание
Предыдущий § Следующий