§5.8. Динамические характеристики исполнительных двигателей постоянного тока

У исполнительных микродвигателей постоянного тока время электромагнитных переходных процессов, связанных с индуктивностью обмоток, значительно меньше времени электромеханических переходных процессов, связанных с моментом инерции ротора. Поэтому на начальном этапе анализа динамических характеристик электромагнитными переходными процессами можно пренебречь и провести этот анализ как и у исполнительных асинхронных микродвигателей на основе уравнения равновесия моментов (2.29).
   Для упрощения анализа принимаем М_ст=0,тогда

М_эм=Jdω/dt

Уравнение прямой линии, проходящей через точки скорости холостого хода и пускового момента М_пα, соответствующие произвольному значению коэффициента сигнала, имеет вид

М_эм=М_пα(1-ω/ω_оα)

т.е. совпадает с (2.41).
    Следовательно, по аналогии можно утверждать, что дифференциальное уравнение движения ротора исполнительных микродвигателей постоянного тока будет совпадать с (2.42), переходные функции – с (2.43) и (2.49),передаточные функции – с (2.47) и (2.48).
    Электромеханическая постоянная времени (см.(2.44)) прямо пропорциональна моменту инерции ротора J, угловой скорости холостого хода ω ₀α и обратно пропорциональна пусковому моменту М_пα.
    При якорном способе управления, как отмечалось ранее, ω_0α=αω_0.мд; M_пα=αМ_п и постоянная времени

τ _м=Jω_0.ид/М_n, (5.57)

где в соответствии с (5.45) ω_0мд/М_n=R_я/(кФ)²
    Электромеханическая постоянная времени τ_м служит характеристикой быстродействия исполнительных двигателей постоянного тока. Чем меньше τ_м, тем двигатель ближе по своим свойствам к идеальному безынерционному звену. Как видно из (5.57), основные меры по уменьшению τ_м следующие:
    1) снижение момента инерции ротора; у микродвигателей с барабанным ротором τ_м лежит в диапазоне 0.035-0,15 с, у микродвигателей с полым немагнитным ротором она снижается до 0,015-0,02 с, а у микродвигателей с дисковым ротором – до 0,005-0,02 с;
    2) увеличение пускового момента за счет совершенствования конструкции, применения лучших магнитных материалов и повышения плотности тока в обмотках.
    Коэффициент передачи двигателя при якорном способе управления

К_дв=ω_0α/U_y=ω_оид/U_уном=1/кФ_ном .    (5.58)

Изложенный анализ динамики исполнительного двигателя постоянного тока проводился без учета статического момента сопротивления на валу двигателя и электромагнитных переходных процессов в обмотке управления. Однако, у некоторых двигателей времена протекания электромагнитных и электромеханических переходных процессов могут оказаться соизмеримыми.
    Кроме этого, в ряде систем автоматического управления электроприводами необходимо иметь возможность анализировать динамические свойства системы при воздействии статического момента сопротивления как внешнего возмущающего воздействия. В качестве математической модели двигателя, учитывающей оба этих фактора, может быть рассмотрена структурная схема двигателя.
    Как известно из теории автоматического управления, структурная схема конкретного устройства представляет собой определенную схему из типовых звеньев: усилительных, апериодических, дифференцирующих, интегрирующих и т.д. Составим такую схему для исполнительного двигателя постоянного тока с якорным управлением (Ф=const).
    При подаче напряжения U _я на обмотку якоря электромагнитные переходные процессы в обмотке определяются законом Кирхгофа:

U_я=e_я+i_яR_я+L_яdi_я/dt ,    (5.59)

где L _я - индуктивность обмотки якоря.
    Это уравнение в операторной форме может быть преобразовано к виду

i_яR_я=(U_я-e_я)/(τ_яp+1),    (5.60)

где τ_я=L_я/R_я.
    Электромеханические переходные процессы определяются уравнением равновесия моментов (2.29), откуда

М_эм-М_ст=Jdω/dt.    (5.61)

Умножим левые и правые части этого уравнения, записанного в операторной форме, на R _я/кФ и преобразуем его с учетом (5.6), (5.10) и (5.57). В результате получаем

i_яR_я-i_стR_я=τ_мре_я,    (5.62)

где i_ст=М_ст/кФ – ток, соответствующий статическому моменту сопротивления М _ст (величина условная, являющаяся частью тока якоря).
    Исходя из уравнений (5.60) и (5.62), составим структурную схему двигателя с выходом по скорости (рис.5.31).

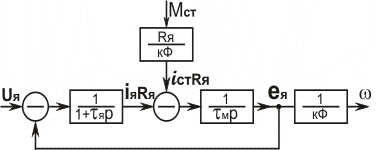
    Рис. 5.31

На входе схемы устанавливаем элемент сравнения, фиксирующий разность напряжения питания и ЭДС якоря. После апериодического звена с постоянной времени τ_я получаем падение напряжения на сопротивлении якоря i_яR_я (см.(5.60)). Разность между ним и падением напряжения от i_ст пропорциональна производной от е_я (см.(5.60)). Чтобы получить саму ЭДС e_я, устанавливаем интегрирующее звено с коэффициентом передачи (1/ τ_м). Сигнал e _я по линии обратной связи подаем на входной элемент сравнения. Для получения в качестве выходной величины угловой скорости ω на пути сигнала е _я в соответствии с (5.6) устанавливаем безынерционное звено с коэффициентом передачи 1/кФ. Возмущающее воздействие М_ст вводим через безынерционное звено с коэффициентом передачи R_я/кФ, получая на входе второго элемента сравнения требуемую величину i_стR_я. Если в качестве выходной величины электропривода используется угол поворота рабочего механизма, связанного с двигателем передаточным устройством с передаточным отношением i_пу, то на выходе структурной схемы должно быть последовательно включено интегрирующее звено с коэффициентом передачи 1/i _пу .

В соответствии с правилами преобразования структурных схем, излагаемыми в курсе "Теория автоматического управления", могут быть получены передаточные функции двигателя по управлению (скорость-напряжение) или возмущению (скорость-момент).
    Например, передаточная функция по управлению будет иметь вид

W(p)=ω(p)/u_я(p)=K_дв/τ_мτ_яp²+τ_мp+1 ,    (5.63),

где коэффициент передачи K_дв=1/кФ, т.е. определяется выражением (5.58).
    Передаточная функция двигателя (5.63) соответствует либо колебательному, либо апериодическому звену второго порядка. Поскольку у двигателей обычно τ_м>4τ_я, то корни характеристического квадратного уравнения знаменателя передаточной функции действительные и разные, и двигатель является апериодическим звеном второго порядка. Если τ_м>> τ_я,то выражение (5.63) может быть сведено к (2.47).
    Коротко остановимся на особенностях динамических характеристик двигателя при полюсном управлении. Дифференциальное уравнение (5.61) будет нелинейным, т.к. величина М_эм пропорциональна произведению переменных Ф и i_я, зависящих от времени. Применяя методы линеаризации, можно записать это уравнение в отклонениях, которое будет представлять собой линейное дифференциальное уравнение третьего порядка. Если пренебречь электромагнитными переходными процессами в якоре и цепи возбуждения, то передаточная функция будет иметь такой же вид, как и при якорном управлении (см.(2.47)). Однако, в отличие от якорного управления, при полюсном управлении значения τ_м и К_кв зависят от конкретного диапазона работы двигателя.