§5.3. Генераторы постоянного тока. Основные характеристики

Генераторы постоянного тока различных систем возбуждения можно объединить в две основные группы: генераторы с независимым возбуждением и генераторы с самовозбуждением, к которым относятся генераторы параллельного, последовательного и смешанного возбуждения.

Генератор независимого возбуждения.

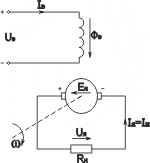
Рис.5.11

Основные статистические характеристики генераторов анализируются при постоянной угловой скорости приводного двигателя.
    Характеристика х.х. E_я= f(I_в)при I_я= 0 генератора независимого возбуждения (рис.5.11) изображена на рис.5.12, а.

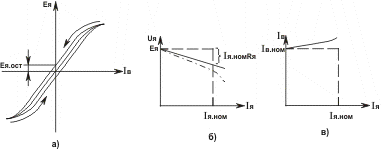
Рис.5.12

Вид такой характеристики можно наиболее просто объяснить на основе формулы (5.6), в которой зависимость потока Ф_вот тока возбуждения I_в определяется петлей намагничивания магнитопровода машины. Характеристика х.х. снимается путем уменьшения от значения примерно 1,25 I_в.ном до (-1,25 I_в.ном) (нисходящая ветвь) и затем увеличения до прежнего значения ( восходящая ветвь ). При I_в=0 в магнитопроводе сохраняется поток остаточного намагничивания и в якоре наводится остаточная ЭДС , составляющая 1–4% от номинальной. За расчетную характеристику х.х. принимается средняя линия.
    Внешняя характеристика строится на основании уравнения равновесия ЭДС и напряжений в цепи якоря, составленного по второму закону Кирхгофа в установившемся режиме:

U_я= E_я- I_яR_я,    (5.11)
где R_я - сопротивления обмотки якоря.

Эта характеристика, построенная без учета реакции якоря, изображена на рис.5.12,б сплошной линией. Характеристика жесткая, так как ток и поток возбуждения не зависят от тока якоря, а падение напряжения I_яR_я на обмотке якоря в номинальном режиме составляет 5–15% от ЭДС. Отклонение внешней характеристики от линейного закона ( штрих-пунктирная линия ) может быть вызвано реакцией якоря. При изменении от R_н до 0 ток якоря непрерывно возрастает.
    Регулировочная характеристика I_в = f(I_я)при U_я =const определяет тот закон, по которому нужно изменять ток возбуждения и соответственно ЭДС якоря, чтобы выходное напряжение сохранялось постоянным при любом токе якоря. Как следует из (5.11) и (5.6), для этого при увеличении тока I_я необходимо увеличивать ток I_в (рис.5.12,в).

Генератор параллельного возбуждения.
    Отличительной особенностью генераторов с самовозбуждением является то, что для возбуждения машины не требуется внешний источник. Принцип самовозбуждения рассмотрим на примере генератора параллельного возбуждения (рис.5.13, а) в режиме х.х.

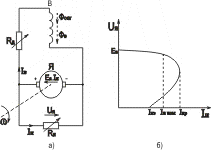
Рис.5.13

Самовозбуждение генератора начинается при выполнении двух условий:
а) в машине имеется поток остаточного намагничивания Ф_ост;
б) полярность включения обмотки возбуждения и направления вращения якоря таковы, что возникающий ток возбуждения создает магнитный поток, направленный согласно с Ф_ост.
    В реальных машинах постоянного тока, хотя бы раз намагниченных, длительное время сохраняется остаточный поток. При вращении якоря поток Ф_ост наводит ЭДС E_{я ост} в обмотке якоря, на обмотке возбуждения появляется напряжение х.х. U_{я ост},и по обмотке возбуждения начинает протекать небольшой ток . Этот ток создает магнитный поток , направленный согласно с Ф_ост и усиливающий Е_я. Усиливается ток возбуждения, и процесс возбуждения продолжается по описанному выше циклу.
     Внешняя характеристика генератора параллельного возбуждения
(рис.5.13, б) , где ток нагрузки I_н=I_я-I_в, отличается от характеристики генератора независимого возбуждения, так как уменьшение U_я при увеличении I_н приводит одновременно к уменьшению I_в и соответственно Е_я. Характеристика становится менее жесткой. Кроме того, в режиме к.з. напряжение U_в=U_я =0 и ЭДС и ток якоря должны быть равны нулю. Однако в реальном генераторе при U_в = 0 поток Ф ≠ 0 и равен потоку Ф_ост. Этот поток наводит ЭДС в якоре, и по нему протекает ток к.з. I_к.з., но значение этого тока к.з. невелико. Таким образом, при изменении R_н от ∞ до 0 токи I_н и I_z соответственно возрастают только до некоторого значения, называемого критическим I_кр., и затем убывают.
    Регулировочная характеристика и характеристика х.х. генератора параллельного возбуждения имеют такой же вид, как и у генератора независимого возбуждения.

Динамические характеристики.
    Динамические характеристики рассмотрим на примере анализа переходных процессов в генераторе независимого возбуждения при подаче на обмотку возбуждения напряжения постоянного тока U_в. При анализе примем допущения о линейности кривой намагничивания машины и отсутствии реакции якоря. Переходный процесс в цепи возбуждения описывается дифференциальным уравнением, составленным по второму закону Кирхгофа:

U_в= i_вR_в + L_в· di_в/dt,    (5.12)
где R_в и L_в - активное сопротивление и индуктивность обмотки возбуждения.

ЭДС якоря определяется в соответствии с ( 5.6 )

e_я=kk_фωi_в , (5.13)
где k_ф - коэффициент пропорциональности между потоком и током возбуждения: Ф= k_фi_в.

Определяем из (5.13) ток и подставляем полученное выражение в (5.12). В результате получаем дифференциальное уравнение, определяющее переходный процесс в генераторе в режиме х.х.:

de_я/dt ·(L_в /R_в) + е_я= kk_фωU_в /R_в.    (5.14)

Переходная функция, определяющая закон изменения во времени выходной величины при ступенчатом изменении входной величины, находится как решение дифференциального уравнения ( 5.14 ) при нулевых начальных условиях ( t = 0, e_я= 0).
   Это экспонента

e_я = E_я (1-e^[t/τв]),    (5.15)
где τ_в – электромагнитная постоянная времени обмотки возбуждения;
E_я = k_u0 U_в- установившееся значение ЭДС якоря.

Коэффициент передачи (усиления) генератора по напряжению в режиме х.х. k_u0 представляет собой отношение приращений ЭДС якоря и напряжения возбуждения в установившемся режиме:

k_u0 = kk_фω /R_в. (5.16)

Уравнение (5.14) в операторной форме с учетом (5.16) имеет вид

τ_вp e_я(p)+ e_я(p)= k_u0U_в(p).    (5.17)

На основании (5.17) записываем передаточную функцию генератора:

W(p) = e_я(p) /u_в(p) = k_u0 /(τ_вp+1).    (5.18)

Из выражения (5.18) видно, что генератор независимого возбуждения в режиме х.х. является апериодическим звеном.
Переходные процессы в режиме нагрузки естественно отличаются от процессов при х.х. При этом характер отличий существенно зависит от характера нагрузки. В качестве примера рассмотрим простейший случай: генератор работает на активную нагрузку Rн. Уравнения, составленные по второму закону Кирхгофа для цепи якоря и нагрузки, при записи в операторной форме имеют вид

e_я(p)= (R_я +L_яp)i_я(p)+u_н(p),   (5.19)

u_н(p) = R_нi_я(p),    (5.20)

где i_я(p) и u_н(p)- операторные изображения тока якоря и напряжения на нагрузке; R_я и L_я - индуктивность и активное сопротивление обмотки якоря. Подставляя i_я(p) из (5.20) в (5.19) и затем из (5.19) в (5.17), получим операторное уравнение

(τ_вp+1)(τ_янp+1)u_н(p) = k_uu_в(p),    (5.21)

где τ_ян = L_я /(R_я+R_н) – постоянная времени цепи якорь–нагрузка;
k_u= k_u0R_н /(R_я+R_н)– коэффициент передачи по напряжению при нагрузке.
На основании (5.21) получаем передаточную функцию

W(p) = u_н(p) /u_в(p) = k_u /(τ_вp+1)(τ_янp+1),    (5.22)

т.е. при активной нагрузке генератор можно представить двумя последовательно включенными апериодическими звеньями.