§2. Уравнения равновесия и схема замещения однофазного трансформатора

Уравнение равновесия МДС.
   Уравнение равновесия МДС составим по 2-му закону Кирхгофа для магнитной цепи трансформатора, изображенной на рис. 1.3. Примем, что положительные направления МДС первичной и вторичной обмоток совпадают с направлением потока Ф₀, тогда

F₁+F₂=U_м   (1.13)

Выражения для МДС F₁ и F₂, через токи в обмотках приведены в §1.1. Падение магнитного потенциала U_м в магнитопроводе трансформатора, работающего с нагрузкой, практически такое же, как при холостом ходе. Объясняется это тем, что магнитный поток Ф₀ при х.х. и нагрузке практически одинаков, практически одинаково и магнитное сопротивление R_м. Однако при х.х. в трансформаторе действует только одна МДС х.х. первичной обмотки F₀=i₀w₁, и можно записать

F₀=U_м   (1.14)

Приравнивая левые части выражений (1.13) и (1.14), получаем

i₁w₁+i₂w₂=i₀w₁. (1.15)

Если токи представляют собой синусоидальные функции времени, то уравнение равновесия МДС (1.15) можно записать в комплексной форме

Ì₁w₁+ Ì₂w₂= Ì₀w₁   (1.16)
или
Ì₁w₁=Ì₀ w₁+(- Ì₂w₂). (1.17)

Как видно из (1.17), первичная МДС имеет две составляющие: I₀w₀ - намагничивающую, необходимую для проведения основного магнитного потока Ф₀ по магнитопроводу; и (-I₂w₂) - необходимую для компенсации размагничивающего действия вторичной обмотки, т.е. передачи энергии с первичной на вторичную сторону трансформатора.

Уравнения равновесия ЭДС и напряжений.
   Уравнения равновесия ЭДС и напряжений в первичной и вторичной цепях трансформатора составим по 2-му закону Кирхгофа для электрических цепей (рис. 1.3)

u₁+e₁+e_σ1= i₁R₁, e₂+ e_σ2=i₂R₂ + i₂z_н   (1.18)

Для случая синусоидальных ЭДС, токов и напряжений можно перейти к комплексной форме записи:

Ù₁= – È₂ – È_σ1+I₁R₁,  Ù₂=È₂+È_σ2–I₂R₂,   (1.19)

где Ù₂= I₂z_н - выходное напряжение трансформатора. Входящие в (1.19) ЭДС самоиндукции E_σ1и E_σ1 на основании (1.2) и (1.3) можно записать в следующем виде:

È_σ1= –jÌ₁ x₁,    E_σ2= –jÌ₂ x₂   (1.20)

где x₁= ωL_σ1 и x₂= ωL_σ2 - индуктивные сопротивления рассеяния обмоток. Преобразуем (1.19) c учетом (1.20):

Ù₁= –È₁ + Ì₁z₁,   Ù₁= –È₂ + Ì₂z₂, (1.21)

где z₁=R₁+jx₁ и z₂=R₂+jx₂ - комплексные сопротивления обмоток.

   Величины I₁z₁ и I₂z₂ – падения напряжения в обмотках. Трансформаторы проектируют так, чтобы энергия передавалась при минимальных потерях в самом трансформаторе. Поэтому в пределах до номинальной нагрузки напряжение питания U₁ уравновешивается в основном ЭДС взаимоиндукции, которая соответствует передаваемой энергии; падение напряжения в обмотке порядка 3-10% от U₁, причем большие значения относятся к трансформаторам меньшей мощности.

Приведенный трансформатор.
   В общем случае в трансформаторе число витков в первичной и вторичной обмотках неодинаково (w₂≠w₁), что затрудняет количественный анализ трансформаторов посредством схем замещения и векторных диаграмм. Поэтому при анализе часто переходят от реального трансформатора к приведенному. Приведенным называют трансформатор, у которого w₂=w₁ и параметры вторичной обмотки пересчитаны таким образом, что мощность на каждом элементе вторичной цепи такая же, как и в реальном трансформаторе. Параметры вторичной обмотки, приведенные к числу витков первичной обмотки, имеют то же буквенное обозначение с верхним индексом “штрих”.
   Поскольку при приведении напряжение и число витков первичной обмотки не изменяются, то основной магнитный поток в приведенном и реальном трансформаторе одинаков. Следовательно, одинакова и ЭДС, приходящаяся на 1 виток вторичной обмотки. Значит:

E₂'=E₂w₁/w₂=K_тE₂=E₁   (1.22)

Полная мощность вторичной цепи I₂'E₂'=I₂E₂, откуда

I₂'=(E₂/E₂')I₂=I₂/K_т   (1.23)

Электрические потери во вторичной обмотке (I₂')²R₂=I₂²R₂, откуда

R₂'=K_т²R₂   (1.24)

По аналогии можно показать, что

x₂'=K_т²x₂,                       
z₂'=K_т²z₂,           (1.25)
z_н'=K_т²z_н.                       

Уравнение равновесия МДС для приведенного трансформатора Ì₁w₁+ Ì₂'w₁=Ì₀'w₁, после сокращения на w₁ преобразуется в уравнение равновесия токов

Ì₁+ Ì₂'=Ì₀   (1.26)

   Уравнения равновесия ЭДС и напряжений принимают вид:

Ù₁= –È₁ + Ì₁'z₁,    Ù₂'=È₂ – Ì₂'z₂'    (1.27)

Схема замещения.
   Представим ЭДС взаимоиндукции E₁ и E₂' в виде падения напряжения на некотором комплексном сопротивлении z_m при протекании тока х.х. (намагничивающего) I₀

È₁= È₂' = – Ì₀z_m   (1.28)

Тогда уравнения (1.26) и (1.27) принимают вид

Ù₁= Ì₀ z_m+ z₁,                             
0= – Ì₀ z_m –Ì₂'z₂' – Ì₂z_n, (1.29)
Ì₁ = Ì₀ + (- Ì₂').                             

Нетрудно показать, что уравнения (1.29) – это уравнения, записанные по 1-му и 2-му законам Кирхгофа для электрической схемы, представленной на рис. 1.6.

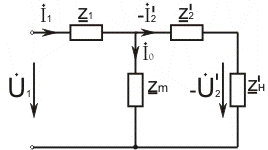
Рис. 1.6

Эта электрическая схема и называется Т-образной схемой замещения трансформатора. Определив расчетным или экспериментальным путем (из опытов холостого хода и короткого замыкания) параметры трансформатора z₁, z₂' и z_m, можно по схеме замещения проводить расчет основных величин и характеристик - токов, напряжений, мощности, КПД и коэффициента мощности.

Несколько слов следует добавить о сопротивлении z_m=R_m+ jx_m, которое называют сопротивлением намагничивающего контура схемы замещения. Действительная часть R_m - это условное активное сопротивление, на котором выделяется мощность, равная магнитным потерям, т.е. R_m= ΔP_м/I₀². Мнимая часть x_m - это индуктивное сопротивление взаимоиндукции обмоток приведенного трансформатора.