назад | ОГЛАВЛЕНИЕ | вперед
6. Электромеханический преобразователь постоянного тока
Рассмотрим
процесс электромеханического преобразования энергии в одном из видов
электрической машины постоянного тока, а именно: в двигателе постоянного тока с
независимым возбуждением.
6.1. Математическое описание процессов
преобразования энергии в двигателе постоянного тока с независимым возбуждением
Необходимым условием
процесса преобразования энергии является протекание переменных токов хотя бы по
части обмоток машины. В двигателе постоянного тока это условие выполняется
работой коллектора, коммутирующего постоянный ток, поступающий от источника
питания, с частотой ωэл, равный угловой скорости вращения ротора.
Таким образом, с точки зрения протекания внутренних процессов двигатель
постоянного тока является машиной переменного тока, а, следовательно, его
моделью является обобщенная электрическая машина (рис. 6.1а).
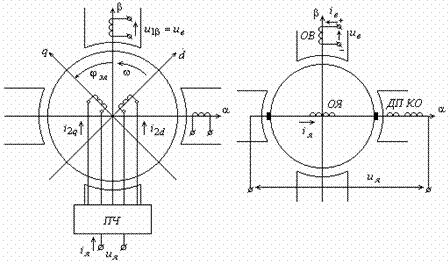
a) б)
Рис.6.1.
Двухфазная модель двигателя постоянного тока c независимым возбуждением в
осях 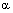 , , 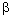 , d, q (а) и в осях , d, q (а) и в осях 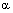 , , 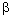
Обмотка статора по оси β включена на постоянное напряжение Uв. Обмотки ротора 2
d и 2q получают питание от
преобразователя частоты ПЧ, осуществляющего коммутацию токов i2d и
i2q в функции угла поворота φэл
с частотой ωэл. Если коммутация
осуществляется механическим коммутатором-коллектором, то мы имеем обобщенную
электрическую модель двигателя постоянного тока. В случае применения в качестве
ПЧ вентильного преобразователя частоты, мы имеем модель вентильного двигателя.
МДС
статора неподвижна в пространстве; она создается током возбуждения iв=
i1β, а ее направление соответствует направлению оси β.
Соответственно и МДС ротора при его вращении со скоростью ω
должна быть неподвижна относительно статора, что возможно лишь при условии
вращения МДС ротора против его вращения со скоростью ω. Это условие выполняется,
если обмотки ротора обтекаются токами, изменяющимися по законам:
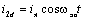 ; ; 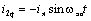 (6.1) (6.1)
МДС ротора в этом случае неподвижна относительно статора, поэтому для математического
описания динамических процессов преобразования энергии в двигателе постоянного
тока целесообразно использовать формулы прямого преобразования координат
обобщенной машины: α, β,
d, q -› α, β
(ωк=0). Для роторных переменных
они имеют вид:
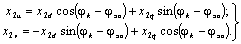 (6.2) (6.2)
Подставив u=α, v=β, 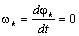 , получим: , получим:
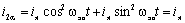 (6.3) (6.3)
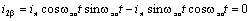 (6.4) (6.4)
Следовательно, в осях α, β действительным
переменным токам обмотки ротора эквивалентна одна якорная обмотка, ось которой
совпадает с осью α и которая обтекается
постоянным током iя. В реальной машине по оси α
расположены также обмотка дополнительных полюсов и компенсационная обмотка.
Поэтому модель двигателя постоянного тока в осях α,
β будет иметь вид (рис. 6.1б).
назад | ОГЛАВЛЕНИЕ | вперед
| 
