3.3. Двухфазно – трехфазное и обратное
преобразования переменных двухфазной модели
Математическое описание составляется для двухфазной модели реальной
машины. Реальные двигатели чаще всего имеют трёхфазную обмотку статора, поэтому
необходимо преобразовать переменные двухфазной модели к переменным трёхфазной
машины.
Один и тот же результирующий вектор МДС может быть создан как
двухфазной, так и трёхфазной обмоткой. Для получения формул
двухфазно-трёхфазных преобразований представим реальные переменные трёхфазной
машины в виде векторов и, будем считать, что преобразованные переменные в осях α и β не равны, а
пропорциональны сумме проекций реальных переменных x1a , x1b, x1c и β
(рис. 3.4).
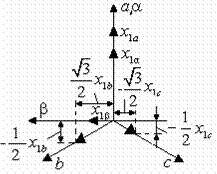
Рис. 3.4. Схема двухфазно – трехфазного преобразования.
Из рис. 3.4 получаем:
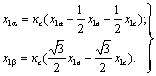 (3.10) (3.10)
где
kc
– согласующий коэффициент пропорциональности, величина которого определяется из
условия инвариантности мощности.
Для трёхфазной
машины, как правило, выполняется условие:
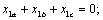
отсюда
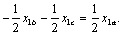
Следовательно,
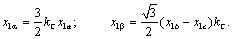 (3.11) (3.11)
Формулы обратного преобразования получим аналогично, воспользовавшись
схемой трехфазно – двухфазного преобразования (рис. 3.5):
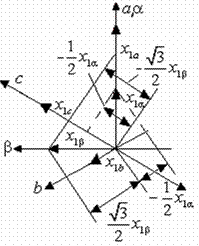
Рис.3.5. Схема трехфазно – двухфазного преобразования.
Из рис.3.5
имеем:
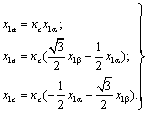 (3.12) (3.12)
Для определения согласующего
коэффициента найдём выражение для мгновенной мощности, потребляемой обмотками
статора из сети:
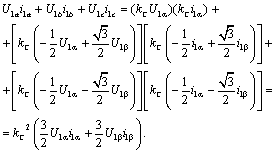
Для выполнения условия инвариантности мощности:
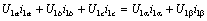
необходимо, чтобы:
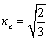 (3.13) (3.13)
Совместим изображающий вектор переменной 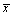 , с осью α модели и с совпадающей с ней осью a реальной машины. При этом , с осью α модели и с совпадающей с ней осью a реальной машины. При этом 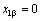 и связь между
амплитудами переменных определяется выражением, полученным при прямом двухфазно
- трёхфазном преобразовании: и связь между
амплитудами переменных определяется выражением, полученным при прямом двухфазно
- трёхфазном преобразовании:
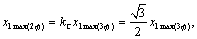 (3.14) (3.14)
где
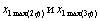 - амплитуды переменной двухфазной модели и трёхфазной
реальной машины. - амплитуды переменной двухфазной модели и трёхфазной
реальной машины.
назад | ОГЛАВЛЕНИЕ | вперед
| 
