назад | ОГЛАВЛЕНИЕ | вперед
2.3. Уравнения движения электропривода
Механическая часть электропривода представляет собой систему твёрдых
тел, движение которых определяется механическими связями между телами. Если
заданы соотношения между скоростями отдельных элементов, то уравнение движения
электропривода имеет дифференциальную форму. Наиболее общей формой записи
уравнений движения являются уравнения движения в обобщенных координатах
(уравнения Лагранжа):
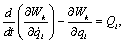 (2.19) (2.19)
где
Wk – запас кинетической энергии системы, выраженный
через обобщенные координаты qi и обобщенные скорости 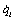 ; ;
Qi– обобщенная сила, определяемая
суммой работ δAiвсех действующих сил на
возможном перемещении 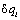 . .
Уравнение Лагранжа можно представить в другом виде:
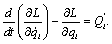 (2.20) (2.20)
Здесь L– функция Лагранжа, представляющая собой разность
кинетической и потенциальной энергий системы:
L=Wk – Wn.
Число уравнений равно числу степеней свободы системы и определяется
числом переменных – обобщенных координат, определяющих положение системы.
Запишем уравнения Лагранжа для <двухмассовой
упругой системы (рис. 2.9).
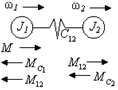
Рис. 2.9. Расчетная схема двухмассовой механической части.
Функция Лагранжа в этом случае имеет вид
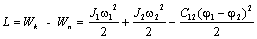
Для определения обобщенной силы 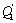 необходимо вычислить
элементарную работу всех приведённых к первой массе моментов на возможном
перемещении: необходимо вычислить
элементарную работу всех приведённых к первой массе моментов на возможном
перемещении:
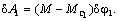
Следовательно, т.к. обобщенная сила 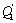 определяется суммой
элементарных работ δA1 на участке δφ1 , то для определения
величины определяется суммой
элементарных работ δA1 на участке δφ1 , то для определения
величины 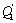 получим: получим:
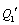 =
= 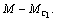
Аналогично, для определения 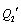 имеем: имеем:
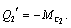
Подставив выражение для функции Лагранжа в (2.20), получим:
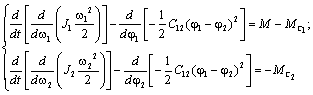
или
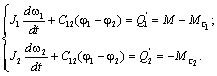
Обозначив 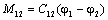 , получим: , получим:
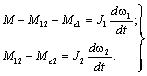 (2.21) (2.21)
Примем механическую связь между первой и второй
массами абсолютно жёсткой, т.е. 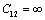 (рис. 2.10). (рис. 2.10).

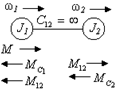
Рис. 2.10. Двухмассовая жесткая механическая система.
Тогда 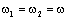 и второе уравнение
системы примет вид: и второе уравнение
системы примет вид:
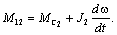
Подставив его в первое уравнение системы, получим:
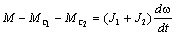
или
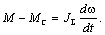 (2.22) (2.22)
Это уравнение иногда называют основным уравнением движения
электропривода. С его помощью можно по известному электромагнитному моменту
двигателя М, моменту сопротивления 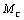 и суммарному моменту инерции и суммарному моменту инерции 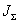 оценить среднее значение ускорения электропривода, рассчитать
время, за которое двигатель достигнет заданной скорости, и решить другие
задачи, если влияние упругих связей в механической системе существенно. оценить среднее значение ускорения электропривода, рассчитать
время, за которое двигатель достигнет заданной скорости, и решить другие
задачи, если влияние упругих связей в механической системе существенно.
Рассмотрим механическую систему с нелинейными кинематическими связями
типа кривошипно-шатунных, кулисных и других подобных механизмов (рис. 2.11).
Радиус приведения в них является переменной величиной, зависящей от положения
механизма: 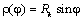 . .
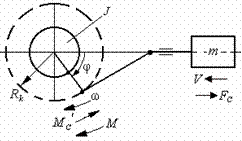
Рис. 2.11. Механическая система с нелинейными кинематическими связями
Представим рассматриваемую систему в виде двухмассовой,
первая масса вращается со скоростью ω и имеет
момент инерции 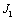 , а вторая движется с линейной скоростью V и
представляет суммарную массу m элементов, жёстко и линейно связанных с рабочим
органом механизма. , а вторая движется с линейной скоростью V и
представляет суммарную массу m элементов, жёстко и линейно связанных с рабочим
органом механизма.
Связь между линейными скоростями ω и V
нелинейная, причём 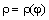 . Для получения уравнения движения такой системы без учёта
упругих связей воспользуемся уравнением Лагранжа (2.19), приняв в качестве
обобщенной координаты угол φ. Определим
обобщенную силу: . Для получения уравнения движения такой системы без учёта
упругих связей воспользуемся уравнением Лагранжа (2.19), приняв в качестве
обобщенной координаты угол φ. Определим
обобщенную силу:
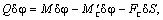
где
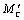 - суммарный момент сопротивления от сил, воздействующих на
линейно связанные с двигателем массы; приведённый к валу двигателя;
- суммарный момент сопротивления от сил, воздействующих на
линейно связанные с двигателем массы; приведённый к валу двигателя;
FC
– результирующая всех сил, приложенная к рабочему органу механизма и линейно
связанным с ним элементам;
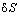 – возможное бесконечно
малое перемещение массы m. – возможное бесконечно
малое перемещение массы m.
Нетрудно видеть, что
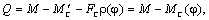
где
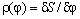 - радиус приведения. - радиус приведения.
Момент статической нагрузки механизма содержит пульсирующую
составляющую нагрузки, изменяющуюся в функции угла поворота φ:
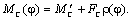
Запас кинетической энергии системы:
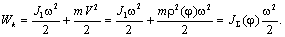
Здесь 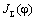 - суммарный приведённый к валу двигателя момент инерции
системы. - суммарный приведённый к валу двигателя момент инерции
системы.
Левую часть уравнения Лагранжа (2.19) можно записать в виде:
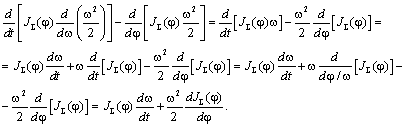
Таким образом, уравнение движения жёсткого приведённого звена имеет
вид:
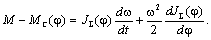 (2.23) (2.23)
Оно является нелинейным с переменными коэффициентами.
Для жёсткого линейного механического звена уравнение статического
режима работы электропривода соответствует 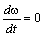 и имеет вид: и имеет вид:
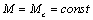 . .
Если при движении 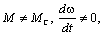 то имеет место или
динамический переходный процесс, или принуждённое движение системы с периодически
изменяющейся скоростью. то имеет место или
динамический переходный процесс, или принуждённое движение системы с периодически
изменяющейся скоростью.
В механических системах с нелинейными кинематическими связями
статические режимы работы отсутствуют. Если 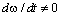 и ω=const, в таких системах имеет место установившийся
динамический процесс движения. Он обусловлен тем, что массы, движущиеся
линейно, совершают возвратно-поступательное движение, и их скорости и ускорения
являются переменными величинами. и ω=const, в таких системах имеет место установившийся
динамический процесс движения. Он обусловлен тем, что массы, движущиеся
линейно, совершают возвратно-поступательное движение, и их скорости и ускорения
являются переменными величинами.
С энергетической точки зрения различают двигательные и тормозные режимы
работы электропривода. Двигательный режим соответствует прямому направлению
передачи механической энергии к рабочему органу механизма. В электроприводах с
активной нагрузкой, а также в переходных процессах в электроприводе, когда
происходит замедление движения механической системы, происходит обратная
передача механической энергии от рабочего органа механизма к двигателю.
назад | ОГЛАВЛЕНИЕ | вперед
| 
