Содержание  Главная (библиотека)
Предыдущий § Следущий

3-16. Параметры асинхронной машины

Параметры рассмотренных схем замещения являются в то же время параметрами асинхронной машины. Они могут быть определены расчетным или опытным путем.

При определении их расчетным путем нужно иметь геометрические размеры машины (наружный и внутренний диаметры статора, то же для ротора, длину воздушного зазора δ между статором и ротором, их длины по оси, а также размеры пазов и зубцов статора и ротора) и ее обмоточные данные (числа витков, их средние длины, сечения проводников и шаги обмоток, числа пазов). Мы будем здесь рассматривать только основные методы расчета параметров, имея в виду установить их связь с геометрическими размерами машины и ее электромагнитными нагрузками.

Под последними понимаются индукции в отдельных участках магнитной цепи машины, линейная нагрузка (условная величина), равная

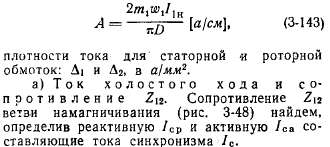Реактивная составляющая I_ср, которая может быть названа намагничивающим током, практически равна реактивной составляющей I_0р тока холостого хода. Для ее определения нужно произвести расчет магнитной цепи машины, т. е. рассчитать н. с. F₀^', могущую создать поток Ф, необходимый для наведения э. д. с. E₁≈0,97U_1н.

Поток Ф находим по (3-77). По потоку Ф, зная сечения зубцов и ярм статора и ротора, определяем индукции в соответствующих участках магнитной цепи. Затем, пользуясь кривыми намагничивания для стали, из которой выполняется статор и ротор, находим для рассчитанных индукций напряженности поля и, умножая их на длины участков, находим магнитные напряжения этих участков.

Наибольшее магнитное напряжение приходится на воздушный зазор, максимальная индукция в котором

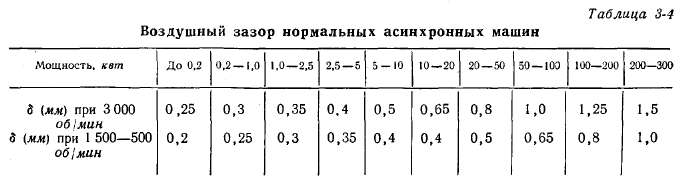зазора вследствие наличия пазов на статоре и роторе: его значение k_δ=l,l÷l,5 (при открытых пазах оно больше, чем при полузакрытых).

Магнитные напряжения стальных участков магнитной цепи при обычных насыщениях составляют в сумме примерно (0,2—0,5) F_δ Следовательно, мы можем написать:

Уравнение (3-149) показывает, что относительное значение тока I_0p зависит главным образом

от δ/τ, так как B_δ /A для нормальных машин

колеблется в сравнительно небольших пределах.

При рассмотрении круговой диаграммы асинхрнной машины (§ 3-17) мы увидим, что cos_φ1 двигателя зависит в основном от тока I_0р, Поэтому для улучшения cosφ₁ воздушный зазор δ выбирается по возможности небольшим; при этом приходится считаться с необходимостью получить механически надежную машину, изготовление и установка которой не вызывают больших затруднений. Значения δ для нормальных машин приведены в табл. 3-4.

Для тихоходных машин (при большом

числе полюсов) величина δ/τ [см. (3-149)] больше, чем для быстроходных (при малом числе полюсов). Этим и объясняется то, что тихоход-

При определении тока холостого хода I₀ нужно учесть еще его активную составляющую, соответствующую механическим потерям Р_меx (на трение вращающихся частей о воздух, в подшипниках и щеток о контактные кольца, если они имеются), а также пульсационным и поверхностным потерям в зубцах ротора и статора Р_с.д (при прохождении зубцов ротора под зубцами статора поле в них пульсирует с большой частотой, то же мы имеем для зубцов статора; кроме того, в сравнительно неглубоких поверхностных слоях зубцов ротора и статора получается неравномерное распределение поля из-за наличия пазов на противоположной части, из

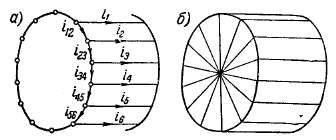Рис. 3-50. Беличья клетка и эквивалентная ей обмотка.

меняющееся при вращении ротора). Указанные потери покрываются за счет механической мощности, развиваемой ротором.

Таким образом, активная составляющая тока холостого хода

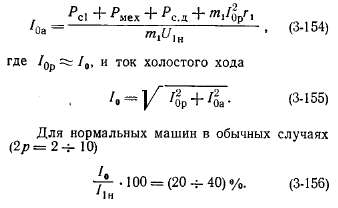б) Активные сопротивления обмоток. Сопротивление постоянному току фазы обмотки статора или фазного ротора рассчитывается по формуле

Активное сопротивление r₂ обмотки фазного ротора при нормальных режимах работы двигателя (при s<5÷10%) может быть принято равным сопротивлению постоянному току. При больших скольжениях для двигателей, имеющих на роторе двухслойную стержневую обмотку (при глубине паза примерно свыше 2 см), r₂ заметно возрастает.

Покажем, как рассчитывается сопротивление r₂ короткозамкнутой

обмотки, выполненной в виде беличьей клетки. Такую клетку можно рассматривать как многофазную обмотку, имеющую число фаз m₂, равное числу пазов ротора Z₂, причем здесь в каждую фазу входит один стержень. На рис. 3-50,а схематически изображена обмотка в виде клетки. Здесь показаны токи в стержнях и частях короткозамыкающего кольца, лежащих между серединами соседних стержней. Эти части следует считать за сопротивления, соединенные многоугольником. Поэтому токи в стержнях i₁, i₂, i₃,... должны рассматриваться как линейные, а токи в частях кольца i₁₂, i₂₃, i₃₄,.. как фазные. В соответствии с этим на рис. 3-51 построена векторная диаграмма токов в соседних частях кольца I_к и в стержне I_с. Сдвиг по фазе токов в соседних стержнях и частях кольца равен:

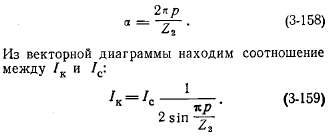Для расчета заменим сопротивления частей кольца, соединенные многоугольником, сопротивлениями, соединенными звездой, после чего получим эквивалентную обмотку, показанную на рис. 3-50,б. Сопротивление фазы r₂ такой обмотки принимается за сопротивление фазы беличьей клетки. Оно определяется из равенства

Рис. 3-51. Векторная диаграмма токов в стержне I_с и соседних частях кольца.

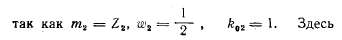также при малых скольжениях (s<5÷7°/₀)r₂ может быть принято равным сопротивлению постоянному току. При больших скольжениях оно заметно возрастает, особенно при глубоких пазах на роторе (§ 3-19,в).

В обычных случаях значение r'₂ близко к значению r₁

в) Индуктивные сопротивления рассеяния обмоток. Определение пото-косцеплений рассеяния, а следовательно, и индуктивных сопротивлений рассеяния х₁ и х₂ представляет собой сложную задачу, точное решение которой не представляется возможным. Поэтому при практических расчетах довольствуются приближенными методами, достаточная точность которых подтверждается опытом.

Индуктивное сопротивление может быть представлено в следующем виде:

Индукционные линии поля рассеяния, например. статора, условно делят на три группы: в соответствии с этим различают три вида рассеяния: пазовое, дифференциальное и лобовых частей обмотки. Если ввести коэффициенты проводимости - пазового рассеяния λ_П, дифференциального рассеяния λ_∂ и рассеяния лобовых частей λ_л, отнесенные к единице длины статора или ротора l, то выражение (3-165) после ряда преобразований примет следующий вид:

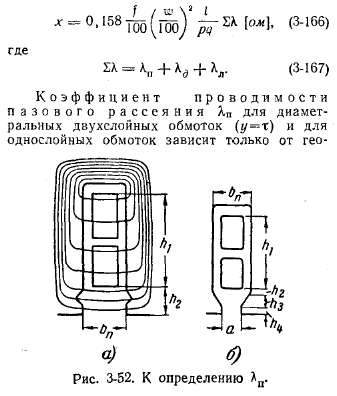метрических размеров паза. Его определяют по потокосцеплению индукционных линий, проходящих поперек паза, с проводниками, лежащими в пазу (рис. 3-52). При этом пренебрегают магнитным сопротивлением индукционных трубок пазового поля рассеяния вне паза и считают, что сопротивление для них определяется только расстояниями между стенками паза в той части, где лежат проводники, и в. части паза над проводниками. Очевидно, что это сопротивление будет тем меньше, чем больше глубина паза (h₁ + h₂ + h₃ + h₄) и чем меньше его ширина b_П.

Для хордовых двухслойных обмоток (у<τ) коэффициент λ_П зависит также и от значения β=у/τ, так как при β<1 в некоторых пазах находятся катушечные стороны, принадлежащие разным фазам (рис. 3-15), вследствие чего общее потокосцепление какой-либо катушечной стороны в этих пазах уменьшается. Следовательно, пазовое рассеяние при у<τ будет меньше, чем при у=τ.

Расчет λ_п производится по формулам:

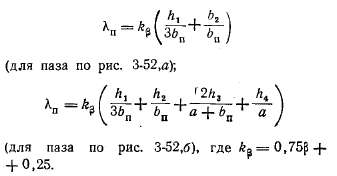Для нормальных машин λ_п = 0,8÷2.

Коэффициент проводимости дифференциального рассеянияλ_∂ в большой степени зависит от числа пазов q₁ (или q₂), шага обмотки. Рассматриваемое рассеяние определяется потокосцеплениями, которые создают высшие гармоники поля, например, статора с его обмоткой. Они наводят в обмотке э. д. с. той же частоты, что и 1-я гармоника поля (§ 3-4,б). Практически они зависят только от тока статора и от проводимости воздушного зазора. Просуммировав указанные э. д. с. и разделив полученную сумму на ток, мы найдем сопротивление х_∂, соответствующее дифференциальному рассеянию (или высшим гармоникам поля). От х_∂ мы можем перейти к коэффициенту λ_∂. Его значение λ_∂=1÷2,5. Оно тем меньше, чем больше число пазов q, длина воздушного зазора δ и чем ближе у к 0,83τ.

Для упрощения расчетов иногда составляют эмпирические формулы, рассматривая вместо дифференциального рассеяния поле рассеяния между соседними коронками (внешними поверхностями) зубцов. Индукционные трубки этого поля проходят через воздушные зазоры и частично через коронки зубцов про-тиволежашей части машины. Их магнитная проводимость определяется в основном длиной воздушного зазора δ.

Коэффициент проводимости рассеяния лобовых частей обмотки λ_л зависит от длины лобовой части.

Его значение λ_л = 0,6÷1,5.

Содержание  Главная (библиотека)
Предыдущий § Следущий