Содержание  Главная (библиотека)
Предыдущий § Следущий

2-19. Несимметричная нагрузка трехфазных трансформаторов

В обычных условиях эксплуатации трехфазной сети нагрузку удается распределить достаточно равномерно на все три фазы. Однако бывают случаи, когда нагрузки фаз сильно отличаются одна от другой, например при питании мощных однофазных печей. При этом системы токов и напряжений получаются несимметричными. Резко несимметричную систему токов получим, очевидно, при несимметричных коротких замыканиях: двухфазном и однофазном.

При исследовании работы трансформаторов, имеющих несимметричную нагрузку, применяется метод симметричных составляющих. Он также широко применяется при исследовании несимметричных режимов работы трехфазных генераторов и двигателей и позволяет наиболее просто и достаточно точно разрешить многие из возникающих при этом вопросов.

а) Метод симметричных составляющих.

Мы здесь сообщим краткие сведения о методе симметричных составляющих. Сущность этого метода состоит в том, что каждый фазный ток (или фазное напряжение) заменяется тремя его составляющими:

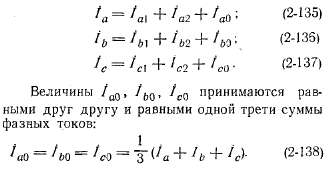Эти величины называются составляющими нулевой последовательности, так как они образуют три равных временных вектора с нулевым сдвигом между ними.

Если из каждого тока данной несимметричной системы вычесть его нулевую составляющую, то получим новую систему токов, сумма которых согласно (2-138) равна нулю:

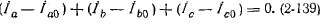Учитывая теперь (2-135) —(2-137), можем написать:

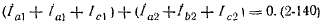Здесь системы токов, стоящих в скобках, будем считать трехфазными симметричными системами. Однако, если принять, что порядки чередования фаз той и другой систем одинаковы, то их сумма даст симметричную систему, что в общем случае не будет соответствовать системе токов уравнения (2-139). Следовательно, мы должны считать, что одна из систем токов (2-140) имеет порядок чередования фаз, обратный по отношению к порядку чередования фаз другой. В соответствии с этим система токов

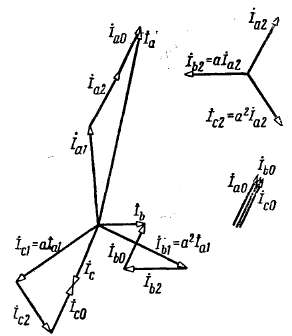
Фазные токи или напряжения в общем случае имеют составляющие всех трех последовательностей; линейные токи (при соединении треугольником) и напряжения могут иметь только составляющие прямой и обратной последовательностей.

В обычных случаях системы симметричных составляющих токов или напряжений можно рассматривать независимо одна от другой и при исследовании несимметричной нагрузки исходить из принципа наложения. Если, например, трехфазная система сопротивлений симметрична, то можно считать, что токи любой последовательности вызовут падения напряжения — активные и реактивные — только той же самой последовательности. В применении к трехфазным трансформаторам мы должны считать Z₁₂ = const, т. е. пренебречь изменением насыщения, или считать Z₁₂ = ∞, т. е. пренебречь током холостого хода.

б) Несимметричная нагрузка трехфазного трансформатора при соединении его обмоток Y/Y₀.

Будем пренебрегать током холостого хода при всех случаях несимметричной нагрузки трансформатора и при всех соединениях его обмоток и будем считать, что нам заданы линейные первичные напряжения и вторичные токи.

В трансформаторах сопротивления Z₁, Z₂ и Z_k для токов прямой последовательности разны тем же сопротивлениям для токов обратной последовательности. Это следует из того, что сопротивления трансформатора не изменятся, если мы при его симметричной на-

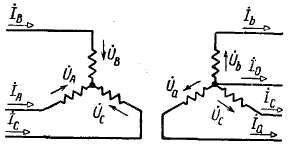Рис. 2-59. Несимметричная нагрузка трансформатора при соединении его обмоток Y/Y₀.

грузке поменяем местами два провода на его первичной стороне.

Рассматриваемому здесь случаю соответствует схема, показанная на рис. 2-59. Согласно этой схеме напишем уравнения токов:

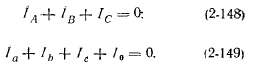Система вторичных токов согласно (2-138) имеет составляющие нулевой последовательности:

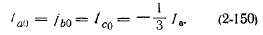Соотношения между первичными и вторичными токами определяются следующим образом.

Обратимся к рис. 2-60, где схематически изображен трансформатор с условными положительными направлениями токов в его обмотках. Так как мы пренебрегаем током холостого хода, то согласно закону полного тока полный ток сквозь любой магнитный контур по сердечнику (например, показанный пунктиром на рис. 2-60) равен нулю. Поэтому, считая ω₁ = ω₂, мы можем написать для контуров, образованных стержнями А—В и А—С и соответствующими ярмами, уравнения:

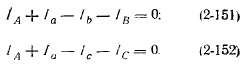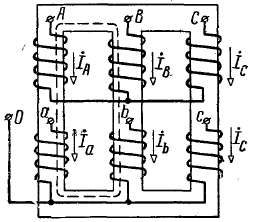
Рис. 2-60. К определению соотношений между первичными и вторичными токами.

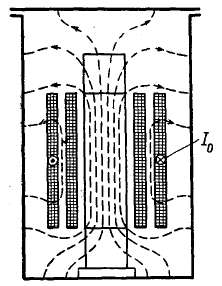Рис. 2-61. Приближенная картина поля, созданного токами нулевой последовательности.

Из этих уравнений и уравнений (2-148) и (2-149) получаем:

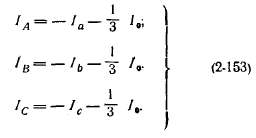Заменяя токи их симметричными составляющими и учитывая (2-150), будем иметь:

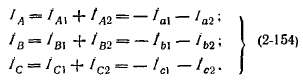Из (2-154) следует, что в трансформаторе при данном соединении его обмоток трансформируются только токи прямой и обратной последовательностей, токи же нулевой последовательности будут иметь место только во вторичной обмотке. Поэтому в магнитном контуре, проходящем по -любому из стержней сердечника и вне его, н. с. обмоток не будут уравновешены.

На рис. 2-62 представлена диаграмма э. д. с., наведенных в фазах обмоток указанными потоками.

Теперь уравнения напряжений для первичной обмотки напишутся следующим образом:

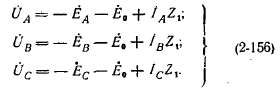Заменим

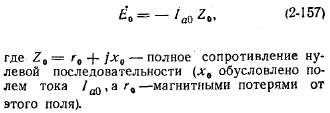Сложив уравнения (2-156) и учитывая при этом (2-155), (2-148) и (2-157), получим:

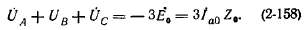Для линейных (междуфазных) напряжений можем написать.

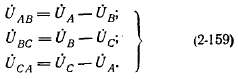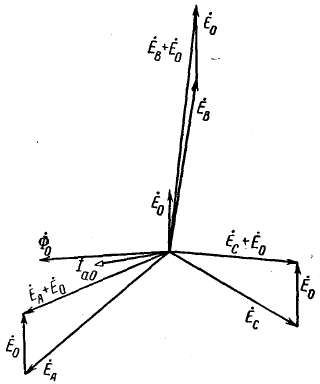
Рис. 2-62. Векторная диаграмма э. д. с. в обмотках трансформатора при несимметричной нагрузке.

Отсюда с учетом (2-158) получим:

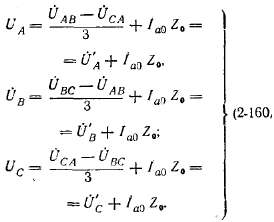
для двух других фаз уравнения напряжений напишутся аналогично:

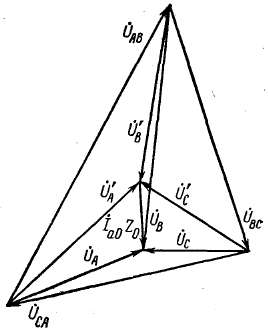
Рис. 2-63. Векторная диаграмма первичных напряжений.

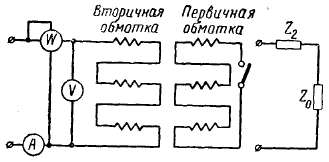Рис. 2-64. Схема для опытного определения сопротивления нулевой последовательности.

рис. 2-64 показана соответствующая схема замещения [см. (2-162)J.

В трехфазной группе, состоящей из трех однофазных трансформаторов, мы не имеем магнитной связи между фазами. В трехфазном броневом трансформаторе эта связь выражена очень слабо. Поэтому при соединении обмоток Y/Y₀ в таких трансформаторах мы имели бы незначительное магнитное сопротивление для потока Ф₀, который здесь полностью проходил бы по стальному сердечнику, и сопротивление r_н было бы очень велико: z_н ≈ z₁₂. Следовательно, даже при малом значении I_а0 мы получили бы значительные смещения потенциалов нулевых точек вторичной и первичной обмоток. Поэтому ни трехфазная группа, ни трехфазный броневой трансформатор с соединением обмоток Y/Y₀ на практике не применяются.

Рассмотрим крайний случай несимметричной нагрузки — однофазное короткое замыкание (рис. 2-65).

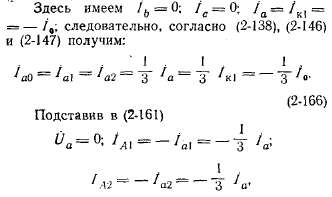получим формулу для тока однофазного короткого замыкания:

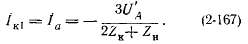Токи в первичной обмотке согласно (2-153) с учетом (2-166):

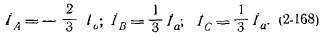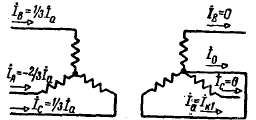
Рис. 2-65. Однофазное короткое замыкание.

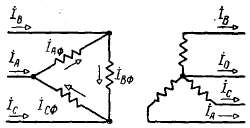Рис. 2-66. Несимметричная нагрузка трансформатора при соединении его обмоток Δ/Y₀.

в) Несимметричная нагрузка трехфазного трансформатора

при соединении обмоток Δ/Y₀.

Рассматриваемому случаю соответствует схема, представленная на рис. 2-66. На вторичной стороне мы имеем такие же токи, как в предыдущем случае (рис. 2-59). Для них действительно уравнение (2-149), т. е. в общем случае система вторичных токов имеет все три симметричные составляющие.

Линейные токи, конечно, не будут иметь составляющих нулевой последовательности:

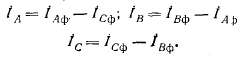
Соответствующая схема представлена на рис. 2-68. Мы здесь рассмотрим случай, когда со вторичной стороны нагружена только одна вторичная обмотка, соединенная звездой с выведенной нулевой точкой. Как и в предыдущем случае, в обмотке, соединенной треугольником, мы будем иметь токи нулевой последовательности; в первичной обмотке будут токи прямой и обратной последовательностей. Следовательно, н. с. обмоток каждой фазы взаимно уравновешиваются и потоки нулевой последовательности практически равны нулю.

Если третья обмотка, соединенная треугольником, используется только как компенсационная для компенсации третьей гармоники в кривой потока, то она должна быть рассчитана на наибольший ток нулевой последовательности с учетом длительности его протекания. Поэтому применение третьей обмотки только как компенсационной в большинстве случаев невыгодно.

д) Несимметричная нагрузка трансформаторов при соединении обмоток Y/Y, Y/Δ, Δ/Y.

Здесь мы не будем иметь во вторичной и в первичной обмотках токи нулевой последовательности; следовательно, не будем иметь для обмотки, соединенной звездой, смещения потенциала нулевой точки относительно центра тяжести треугольника линейных напряжений. При

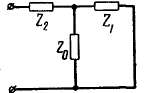Рис. 2-67. Схема замещения для Z_н трансформатора при соединении его обмоток Δ/Y₀.

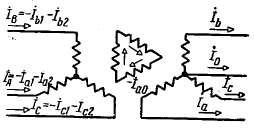Рис. 2-68. Несимметричная нагрузка трехобмоточного трансформатора при соединении обмоток Y/Δ/Y.

данных соединениях обмоток мы можем рассматривать первичную и вторичную обмотки каждой фазы как независимый однофазный трансформатор. Уравнения напряжений (2-161), (2-163) и (2-164), если в них взять I_α0 = 0, могут быть использованы при определении вторичных напряжений для заданных первичных напряжений, вторичных токов (при известных параметрах трансформатора Z_k = r_k+jx_k). При помощи тех же уравнений могут быть определены фазные и линейные токи при двух-' фазных коротких замыканиях.

Содержание  Главная (библиотека)
Предыдущий § Следущий