Содержание  Главная (библиотека)
Предыдущий § Следущий

2-9. Потери и коэффициент полезного действия

При работе трансформатора в нем возникают потери — магнитные и электрические.

Магнитные потери, или потери в стали Р_с, принимаются, как отмечалось, равными потерям холостого хода Р₀. Они зависят от частоты тока, от индукций В_с в стержне и В_я в ярме сердечника, а также от весов стержней и ярм. Для уменьшения магнитных потерь и реактивной составляющей тока холостого хода сечение ярма берут несколько больше (на 5—10%) сечения стержня. Потери Р₀ приблизительно пропорциональны квадрату индукции (В²) и частоте тока в степени 1.3 (f^1,3).

Электрические потери, или потери короткого замыкания, пропорциональны квадрату тока.

Коэффициент полезного действия (к. п. д.) трансформатора имеет высокие значения: от 0,96 при S ≈ 5 ква до 0,0995 при номинальной мощности, составляющей десятки тысяч киловольт-ампер. Поэтому определение его непосредственным методом по формуле

где Р₂ — полезная (вторичная) мощность; Р₁ — затраченная (первичная) мощность, практически не может дать точных результатов.

Так как потери в трансформаторе невелики, то следует определять к. п. д. трансформатора косвенным методом и пользоваться при этом формулой

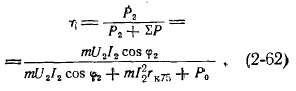
В правой части (2-63) переменной величиной является только β. Обычным путем можно найти максимум функции η = f(β). Для этого приравняем ее первую производную нулю:

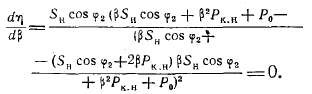В полученной дроби знаменатель при реальных значениях β не может быть равным бесконечности. Поэтому нужно приравнять нулю числитель. Отсюда найдем, что к. п. д. будет максимальным, когда потери короткого замыкания будут равны потерям холостого хода:

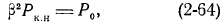т. е. при равенстве переменных потерь постоянным потерям (при изменении нагрузки практически изменяются только потери короткого замыкания).

Для трансформаторов, выпускаемых заводами Советского Союза, имеем:

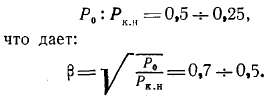Следовательно, к. п. д. получается максимальным при нагрузке, составляющей 50—70% от номинальной. Такая нагрузка обычно и соответствует средней нагрузке при эксплуатации трансформатора.

При вычислении к. п. д. пользуются формулой

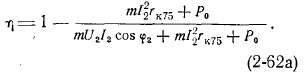
Содержание  Главная (библиотека)
Предыдущий § Следущий