Содержание
Предыдущий § Следующий

Глава шестнадцатая НЕСИММЕТРИЧНАЯ НАГРУЗКА ТРАНСФОРМАТОРОВ

§ 16-1. Применение метода симметричных составляющих

Общие положения. На практике встречаются случаи, когда отдельные фазы трансформатора нагружены несимметрично (неравномерное распределение осветительной нагрузки по фазам, приключение мощных однофазных приемников и т. д.). Кроме того, в электрических сетях, питающихся от трансформаторов, случаются несимметричные короткие замыкания (однофазные на землю или на нулевой провод и двухфазные). При анализе несимметричных режимов работы трансформатора будем предполагать, что трансформатор имеет симметричное устройство, т. е. все три фазы одинаковы в магнитном и электрическом отношении.

Как известно, общим методом анализа несимметричных режимов является метод симметричных составляющих. Согласно этому методу, трехфазная несимметричная система токов /_а, /_ь, /_с разлагается на системы токов прямой (/_а1, /_Ь1, /_с1), обратной (/_о2. Дг. Дг) и нулевой (/_а0, /_й0. /_с0) последовательностей (рис. 16-1). Векторы токов прямой последовательности /_а1, /_и, /_е1 равны по величине и чередуются со сдвигом по фазе на 120° в направлении движения часо-

вой стрелки. Векторы токов обратной последовательности /_аа, 1^, /_е2 также равны по величине, но чередуются со сдвигом по фазе на 120° в направлении, обратном движению часовой стрелки. Векторы

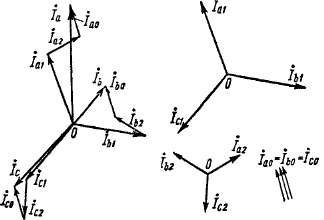Рис. 16-1. Симметричные составляющие трехфазных токов

токов нулевой последовательности /_а0, /_ьо, /_с0 равны по величине и совпадают по фазе. При этом

Симметричные составляющие фазы а можно брать за основные и тогда, согласно выражениям (16-1) и (16-2), можно также написать

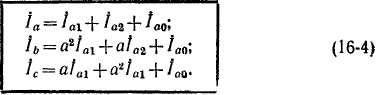
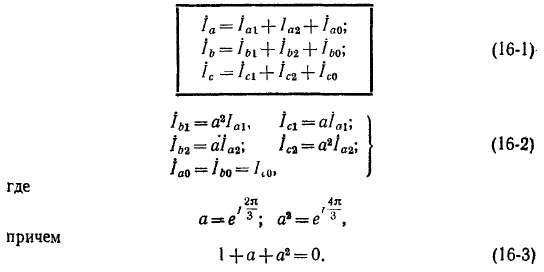
Решая уравнения (16-4) относительно /_а1, /_а2 и /_а0, получаем

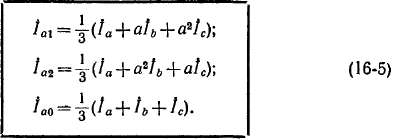На основании последнего равенства (1Б-5)

Таким образом, при наличии токов нулевой последовательности сумма токов трех фаз отлична от нуля.

Совершенно аналогичные соотношения действительны также для несимметричной системы напряжений фаз 0'„, Оь, О_е и их симметричных составляющих.

Очевидно, что применение метода симметричных составляющих основано на принципе наложения. Ниже предполагается, что для всех участков магнитной цепи трансформатора f* == const, чем и обусловлена возможность применения этого принципа.

Будем также предполагать, что числа витков первичной и вторичной обмоток равны \w_x = w₂) и поэтому нет надобности различать неприведенные и приведенные вторичные величины и обозначать последние штрихами. Общность получаемых при этом результатов не нарушается, так как всегда можно произвести соответствующие пересчеты. Первичные фазные величины будем обозначать индексами А, В, С, а вторичные — индексами а, Ь, с.

Схемы замещения и сопротивления трансформатора для токов прямой и обратной последовательности. В предыдущих главах рассматривалась работа трансформатора при симметричной нагрузке, когда токи фаз трансформатора составляли симметричную систему:

1_Ь = а²! _а; 1_С = at _а. Если подставить эти значения /_й и /_с в (16-5), то получим

» at — 'а\ ' ач. — 0; lao ~ 0»

т. е. в этом случае существуют только токи прямой последовательности. Поэтому все изложенное в предыдущих главах соответствовало работе трансформатора с токами прямой последовательности. Если у трансформатора, работающего с симметричной нагрузкой, переменить местами два зажима со стороны высшего напряжения

(например, В и С) и со стороны низшего напряжения (например, b и с), то режим работы потребителей и самого трансформатора не изменится. Однако чередование векторов токов фаз трансформатора при этом изменится на обратное, т. е. будет соответствовать токам обратной последовательности. Следовательно, токи обратной последовательности трансформируются из одной обмотки в другую так же, как и токи прямой последовательности.

Таким образом, поведение трансформатора по отношению к токам прямой и обратной последовательности одинаково. Поэтому схемы замещения рис. 14-5 и 14-6 действительны как для токов прямой, так и для токов обратной последовательности. Сопротивление трансформатора пс отношению к токам этих последовательностей также одинаково и равно сопротивлению короткого замыкания Z_K.

Можно отметить, что любое симметричное статическое (не имеющее вращающихся частей) трехфазное устройство (трансформатор,

линия передачи, электрическая печь и т. д.) имеет равные сопротивления для токов прямой и обратной последовательности.

Токи и потоки нулевой последовательности в трансформаторах. В обмотках, соединенных звездой,токи нулевой последовательности могу? возникать только при наличии нулевого провода (рис. 16-2, а)* так как /_о0, До. До равны по величине и по фазе, в каждый момент времени направлены во всех фазах одинаково и поэтому цепь этих токов может замыкаться только через нулевой провод. В нулевом проводе протекает ток

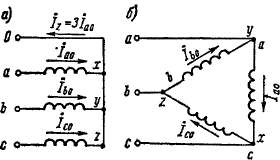Рис. 16-2. Токи нулевой последовательности в обмотках, соединенных в звезду с нулевым проводом (а) и в треугольник (б)

Роль нулевого провода может играть также земля, если нулевая точка трансформатора заземлена.

В обмотках, соединенных треугольником (рис. 16-2, б), тюки До ⁼ До ⁼ До составляют ток, циркулирующий по замкнутому контуру. Линейные токи, которые представляют собой разности токов смежных фаз, в данном случае не содержат токов нулевой последовательности. В этом можно убедиться, вычисляя, например, Д — Д по соотношениям (16-4). Поэтому токи нулевой последовательности в обмотке, соединенной треугольником, могут воз-

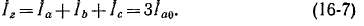
никать только в результате индуктирования их другой обмоткой трансформатора.

Токи нулевой последовательности создают во всех фазах потоки нулевой последовательности Ф_Оп, которые во времени совпадают по фазе. В этом отношении они аналогичны третьим гармоникам потока трехфазных трансформаторов, возникающим вследствие насыщения магнитной цепи (см. § 13-1), и проходят в сердечниках таким же образом (см. рис. 13-6). В трансформаторах броневой и бронестержневой конструкции, а также в трехфазной группе однофазных трансформаторов Ф_Оп замыкаются по замкнутым стальным сердечникам (см. рис. 13-6, а и б). Поэтому в данном случае магнитное сопротивление для потоков Ф_Оп мало и уже небольшие токи 1_а0 = До = /_с0 способны создавать большие потоки Ф_Оп. Действительно, если ток f_a0 равен току холостого хода трансформатора, то поток Ф<,„ равен нормальному рабочему потоку трансформатора. В трехстержневом трансформаторе потоки нулевой последовательности направлены в каждый момент времени во всех стержнях одинаково и поэтому замыкаются от одного ярма к другому через масло и бак трансформатора (см. рис. 13-6, $). В этом случае магнитное сопротивление для Ф_ви относительно велико, а в стенках бака индуктируются вихревые токи и возникают потери.

Из сказанного следует, что теки и потоки нулевой последовательности в трансформаторах различной конструкции и с различными соединениями обмоток проявляются и действуют аналогично третьим гармоникам намагничивающего тока и потока. Разница заключается лишь в том, что первые изменяются с основной, а вторые — с трехкратной частотой.

Схемы замещения и сопротивления трансформатора для токов нулевой последовательности. Потоки, создаваемые токами нулевой последовательности, индуктируют в первичной и вторичной обмотках э. д. с. само- и взаимной индукции, которым соответствуют собственные и взаимные индуктивные сопротивления обмоток. Если привести обмотки к одинаковому числу витков, то для токов нулевой последовательности можно составить подобную же Т-образную схему замещения (рис. 16-3), как и для токов прямой последовательности. Параметры отдельных элементов схемы замещения при этом зависят от устройства магнитной цепи и обмоток трансформатора, но не зависят от схемы соединения обмоток. От нее зарисит лишь вид схем замещения относительно выходных зажимов и сопротивление нулевой последоваяедйноети в целом.

В трансформаторе с соединением обмоток Y_Q/Y₀ токи нулевой последовательности могут существовать как в самих первичной и вторичной обмотках, так и во внешних первичной и вторичной цепях трансформатора, Поэтому в данном случае схема замещения

нулевой последовательности (рис. 16-3, а) по своему виду ничем не отличается от схемы замещения прямой последовательности. В случае соединения обмоток по схеме Y/Y_o токи нулевой последовательности в обмотке без нулевого провода существовать не могут, и поэтому схема замещения нулевой последовательности со стороны этой обмотки разомкнута (рис. 16-3, б). Однако на зажимах обмотки без нулевого провода существует фазное напряжение нулевой последовательности 0_Ао, индуктируемое током нулевой последователь-

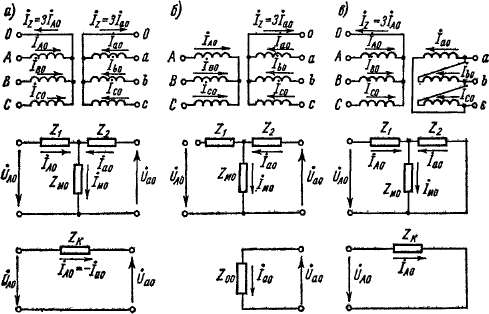Рис. 16-3. Схемы замещения трансформатора для токов нулевой последовательности

йости обмотки Y_o. У трансформатора с соединением обмоток A/Y_o токи нулевой последовательности также могут существовать в обеих обмотках, но обмотка, соединенная треугольником, замкнута относительно этих токов накоротко и токи нулевой последовательности в ее внешней цепи существовать не могут. Поэтому в данном случае зажимы схемы замещения нулевой последовательности (рис. 16-3, в) со стороны обмотки А замкнуты накоротко. Сопротивления

схем замещения рис. 16-3 содержат активные сопротивления г_ъ г₂ и индуктивные сопротивления рассеяния x_it x₂, которые практически не отличаются от значений этих сопротивлений для токов прямой и обратной последовательности.

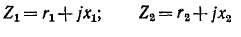
Сопротивление намагничивающей цепи Z_m0 в броневых, бронестержневых и групповых трансформаторах также практически не отличаются от сопротивления намагничивающей цепи 2_мдля токов прямой последовательности, так как в этих случаях потоки нулевой последовательности также замыкаются по замкнутым стальным сердечникам. Если токи нулевой последовательности протекают в обеих обмотках, то в этом случае намагничивающий ток составляет небольшую долю полного тока нулевой последова* тельности. Поэтому им можно пренебречь, и тогда получим упрощенные схемы замещения, изображенные в нижней части рис. 16-3, а и в. При этом Z_K = Z_x + Z₂. У трехстержневого трансформатора Z_m0 в десятки и сотни раз меньше Z_M, так как поток нулевой последовательности замыкается по воздуху. В этом случае обычно Z_m0 «^ ^(7т 15) Z_K и без большой погрешности также можно пользоваться упрощенными схемами замещения рис. 16-3, а и в.

Э. д. с. Е_а0, индуктируемая основным потоком нулевой последовательности, равна с обратным знаком напряжению на зажимах намагничивающей цепи схемы замещения:

Сопротивление нулевой последовательности Z_On трехфазного трансформатора в целом представляет собой сопротивление трансформатора токам нулевой последовательности, замеренное со стороны одной обмотки, когда все выходные зажимы второй обмотки замкнуты накоротко. Для схемы рис. 16-3, а при этом получаются два значения сопротивления нулевой последовательности, которые практически .равны (имеется в виду, что обмотки приведены к одинаковому числу витков). Для броневых и бронестержневых и групповых трансформаторов Z^ J> Z_x «=* Z₂, и поэтому

Однако и для стержневых трансформаторов соотношение (16-9) справедливо с достаточной для практических расчетов точностью. Таким образом, в этих случаях Z_On мало.

Для схемы рис. 16-3, б определение Z_On со стороны обмотки Y не имеет смысла, так как 1_Ао — О, а ео стороны обмотки Y_o

При этом для броневых, бронестержневых и групповых трансформаторов Z_m0 = Z_M, поэтому Z_On велико и равно сопротивлению холостого хода для токов прямой последовательности (см. § 14-5):

Для трехстержневого трансформатора в случае соединения обмоток по схеме рис. 16-3, б Z_K < Z_On <; Z_o.

Для рис. 16-3, в определение Z_On со стороны обмотки А также не имеет смысла, так как в линейных токах составляющей нулевой последовательности не содержится, а со стороны обмотки Y_o

Таким образом, для различных трансформаторов Z_On изменяется в пределах от сопротивления короткого замыкания Z_K до

сопротивления холостого хода Z_o.

При экспериментальном определении Z_On в обмотке необходимо создать токи

/«=/₆ = /_с = /оп. (16-14)

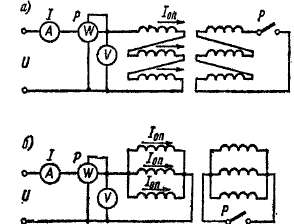
Для этого три фазы обмотки можно соединить последовательно (рис. 16-4, а) или параллельно (рис. 16-4, б). Первый случай • соответствует включению источника напряжения в рассечку треугольника, а второй — его включению в нулевой провод, когда обмотка соединена в

звезду. Схема соединений вторичной обмотки может иметь также два варианта. Последовательное соединение фаз (рис. 16-4, а) более предпочтительно, так как соблюдение равенства (16-14) при этом обеспечено при всех условиях. Рубильник Р на схемах рис. 16-4 должен быть замкнут в случае, когда во вторичной обмотке возможно существование токов нулевой последовательности (соединение Д или Y_o с незначительным сопротивлением нулевого провода), и разомкнут при соединении Y.

При схеме соединений рис. 16-4, а

Рис. 16-4. Схемы опытного определения сопротивлений нулевой последовательности

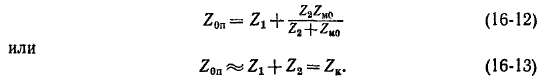
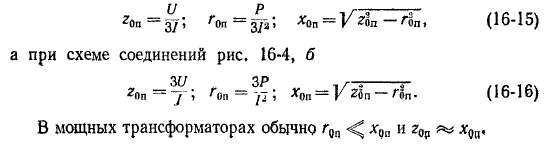
§ 16-2. Физические условия работы трансформаторов при несимметричной нагрузке

Несимметричная нагрузка при отсутствии токов нулевой последовательности. Токи нулевой последовательности отсутствуют в случае, когда сеть не имеет нулевого провода или когда этот провод не нагружен током. Так как токи прямой и обратной последовательности во всех случаях одинаковым образом трансформируются из одной обмотки в другую и сопротивления трансформатора для этих токов одинаковы, то их действие можно учитывать совместно. Поэтому при отсутствии токов нулевой последовательности необходимость разложения токов и напряжений на симметричные составляющие отпадает.

Если w_t = w₂ и намагничивающий ток принять равным нулю, то первичные и вторичные токи прямой последовательности в каждой фазе равны по величине и обратны по знаку. Это же справедливо и для токов обратной последовательности, а значит, и для суммы токов прямой и обратной последовательности. Поэтому при принятых предположениях в рассматриваемом случае полные токи фаз

Если учитывать также намагничивающие токи, то равенства (16-17) действительны для нагрузочных составляющих токов,

Из сказанного следует, что н. с. и токи первичных и вторичных обмоток уравновешиваются в каждой фазе и на каждом сердечнике по отдельности. Поэтому влияние одних фаз на другие отсутствует и каждую фазу можно рассматривать по отдельности, причем для каждой фазы действительны схемы замещения вида рис. 14-5 и 14-6 с одинаковыми параметрами, которые можно использовать для расчета соотношений между напряжениями, токами и другими величинами каждой фазы. Связи же между отдельными фазами трансформатора необходимо рассматривать только для установления соотношений между линейными и фазными величинами в зависимости от вида схем соединений обмоток.

При несимметричной нагрузке падения напряжения AU в отдельных фазах трансформатора различны. Но если токи отдельных фаз не превышают номинальных значений, то при /_0П| = 0 величины AU относительно малы, так как сопротивление Z_K трансформатора относительно мало. Отсюда можно сделать вывод, что несимметричная нагрузка трансформатора при /_Оп = 0 не вызывает значительного искажения симметрии фазных и линейных напряжений. Поэтому при /₀„ = 0 больших осложнений в работе трансформатора не возникает. Отметим, что, согласно ГОСТ 3484—65, трехфазная система напряжений или токов считается практически симметричной,

если составляющая обратной последовательности равна не более 5% составляющей прямой последовательности.

На рис. 16-5, а, б, в и г показано распределение токов в фазах трансформатора и линейных проводах в случае коротких замыканий между вторичными линейными зажимами трансформатора. Указанное распределение токов действительно также при различных характерах нагрузки, когда /_Оп = 0. Рис. 16-5, а соответствует симметричной нагрузке.

Несимметричная нагрузка при наличии токов нулевой последовательности. Токи нулевой последовательности возникают обычно

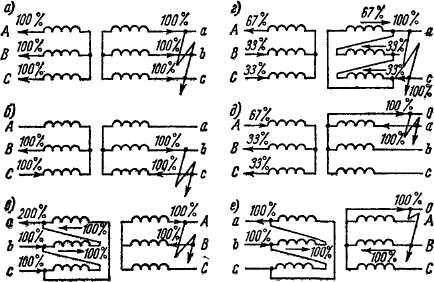Рис. 16-5. Токораспределение в обмотках трансформаторов с различными схемами соединений обмоток при различных видах коротких замыканий

тогда, когда вторичная обмотка соединена в звезду с нулевым проводом и между нулевым и линейным проводами включаются однофазные потребители, а также при однофазном коротком замыкании на вторичной стороне такого трансформатора.

Ниже будем предполагать, что система первичных напряжений Трансформатора остается симметричной.

Необходимо различать два случая: 1) токи нулевой последовательности возникают в обеих обмотках трансформатора и 2) они возникают только в одной обмотке,

В первом случае (трансформаторы с соединением обмоток Y₀/Y_D и Д/Yo) намагничивающим током нулевой последовательности можно пренебречь, так как он будет составлять небольшую долю полного тдка нулевой последовательности, и

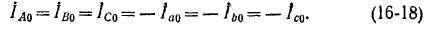
Поэтому н. с. токов нулевой последовательности взаимно уравновешиваются в каждой фазе трансформатора, сопротивление нулевой последовательности Z_On = Z_K и для этого случая применима упрощенная схема замещения (рис. 16-3, айв снизу). Поскольку вследствие этого токи всех последовательностей трансформируются одинаковым образом из одной обмотки в другую и для них существуют одинаковые схемы замещения с одинаковыми параметрами, то в данном случае также, вообще говоря, нет надобности раскладывать полные токи и напряжения фаз на симметричные составляющие. Нулевые составляющие вторичного напряжения £/_а0 в данном случае возникают только за счет относительно небольших падений напряжения Zj_Ao. Поэтому в трансформаторах с соединением обмоток A/Y_o при несимметричной нагрузке система трехфазных напряжений искажается относительно слабо.

Во втором случае (трансформаторы с соединением обмоток Y/Y_o) токи нулевой последовательности /_а0 протекают только

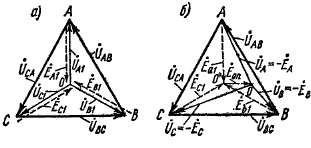во вторичной обмотке и являются чисто намагничивающими, так как они не уравновешены токами 1_Ао в первичной обмотке. Э. д. с, нулевой последовательности

Рис. 16-6. Искажение системы фазных напряжений в трансформаторе с соединением обмоток Y/Y_o при наличии токов нулевой последовательности

поэтому могут достичь больших значений. Например, для группового трансформатора, у которого Z_m0 = Z_a, уже при 1_а0 = /₀ да да (0,02 -s- 0,05) /_н э. д. с. Е_Оа да 0_в. В результате система фазных э. д. с. и напряжений сильно искажается, в чем можно убедиться из нижеследующего.

Пусть первичная обмотка (Y) трансформатора с соединением обмоток Y/Y_o приключена к сети, линейные напряжения которой Uab, Ubcj Uca симметричны и являются поэтому напряжениями прямой последовательности. Векторная диаграмма первичных линейных и фазных напряжений на холостом ходу при этом имеет вид, показанный .на рис. 16-6, а. Фазные э. д. с. Ё_Аг тш —О_АХ, Ёрг да ^ — &вь Ёа & —Оа также представляют собой симметричную систему прямой последовательности. Векторная диаграмма системы вторичных напряжении на холостом ходу будет иметь совершенно такой же вид.

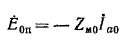
Пусть теперь вторичная обмотка (Y_o) нагружена несимметрично, с содержанием токов всех последовательностей. Вторичные токи прямой и обратной последовательности трансформируются на первичную обмотку, магнитно уравновешены и вызывают только относительно малые падения напряжения. Однако не уравновешенные со стороны первичной обмотки вторичные токи Нулевой последовательности индуктируют в обеих обмотках э. д. с Е_Оа, которые складываются с э. д. с. прямой последовательности, в результате чего полные фазы э. д. с. будут

Система первичных фазных напряжений при пренебрежении падениями напряжений определяется векторами:

и будет при этом сильно искажена, а нулевая точка на диаграмме сместится на величину Ёоа ^и не будет совпадать с центром тяжести треугольника линейных напряжений (рис. 16-6, б). Диаграмма вторичных напряжений будет иметь аналогичный вид. Направление векторов Ё_Оп зависит от фазы токов /_а0 и определяется условиями нагрузки. На величину линейных напряжений напряжения нулевой последовательности не влияют, так как в разностях 0_аЬ = О_а — —Оь и т. д. нулевые составляющие исчезают.

Таким образом, в трансформаторе с соединением обмоток Y/Y_o токи нулевой последовательности могут вызвать сильные искажения величин фазных напряжений, что неприемлемо и опасно для однофазных потребителей.

В групповых, броневых и бронестержневых трансформаторах с соединением обмоток Y/Y_o сильное искажение системы фазных напряжений возникает уже при незначительных по величине токах нулевой последовательности. Поэтому соединение Y/Y_o в этих транс* форматорах обычно не применяется, а если все же в отдельных случаях по каким-либо причинам обе обмотки желательно соединить в звезду, то на каждой фазе выполняется еще третья, или так назы» ваемая третичная, обмотка, которая соединяется в треугольник. Если эта обмотка предназначена только для уравновешивания токов нулевой последовательности, то концы ее наружу на выводятся. Если же она рассчитана также для нагрузки и ее концы выводятся наружу, то получается трехобмоточный трансформатор (см. § 18-1). Отметим, что наличие нулевого провода или заземления с обеих сторон трансформатора с соединением обмоток Y_o/Y_o не дает гарантии-уравновешивания токов нулевой последовательности, так как сопротивление первичного контура для этих токов может оказаться большим.

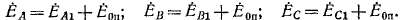
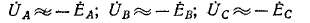
У трехстержневых трансформаторов с соединением обмоток Y/Y_o искажение системы фазных напряжений при наличии токов нулевой последовательности меньше, так как Z_m0 <; Z_u. В СССР такие трансформаторы строятся мощностью до 6000 кв -а. При этом, согласно ГОСТ 11677—67, требуется, чтобы ток в нулевом проводе не превышал 25% номинального тока. Тогда ток нулевой последовательности не будет превосходить 25:3 = 8,3% номинального тока.

Отметим, что трансформаторы с соединением обмоток «звезда — зигзаг с нулевым выводом» хорошо переносят нагрузки с содержанием токов нулевой последовательности, так как эти токи уравновешиваются во вторичных обмотках на каждом сердечнике, поскольку на каждом сердечнике имеются две половинки фаз вторичной обмотки, которые обтекаются токами нулевой последовательности в противоположных направлениях (см. рис. 12-22).

Распределение токов по фазам первичной и вторичной обмоток трансформаторов с соединением Y/Y_o и A/Y_o при однофазных коротких замыканиях и однофазных нагрузках представлено на рис. 16-5, д и е.

Содержание
Предыдущий § Следующий