§4.2.Вращающиеся (поворотные) трансформаторы

Вращающимися трансформаторами называют электрические микромашины переменного тока, предназначенные для преобразования угла поворота Θ в напряжение, пропорциональное некоторым функциям угла (например, sinΘ или cos Θ) или самому углу поворота ротора.
   Вращающиеся трансформаторы (ВТ) применяют в аналого-цифровых преобразователях «угол – амплитуда –код» и «угол – фаза – код» цифровых следящих систем и систем программного управления промышленными роботами и автоматами; в системах дистанционной передачи угла повышенной точности и в электромеханических вычислительных устройствах, предназначенных для решения тригонометрических задач и преобразования координат.
   Возможны несколько режимов работы вращающихся трансформаторов в зависимости от схемы включения их обмоток:
1) синусно – косинусные ВТ, у которых выходное напряжение одной обмотки пропорционально синусу угла поворота ротора, а другой обмотки – косинусу угла поворота ротора (СКВТ);
2) линейные ВТ, у которых выходное напряжение пропорционально углу поворота ротора (ЛВТ); получение линейной в определенном угловом диапазоне выходной характеристики сводится к аппроксимации прямой линии функцией типа f(Θ)=sinΘ/(1+C*cosΘ), где С – постоянный коэффициент;
3) масштабные ВТ, у которых выходное напряжение пропорционально входному, и коэффициент пропорциональности (масштаб) определяется углом поворота ротора;
4) датчики и приемники трансформаторных дистанционных передач угла (ВТДП), выполняющие функции, аналогичные трансформаторным сельсинам;
5) преобразователи координат, осуществляющие поворот осей декартовой системы координат или переход к полярной системе координат (построители);
6) индукционные фазовращатели, осуществляющие преобразование пространственного угла во временной.
   Основным требованием, предъявляемым к вращающимся трансформаторам, является максимальная точность преобразования угла в напряжение по заданному функциональному закону. В зависимости от условий применения к вращающимся трансформаторам может быть предъявлен ряд специальных требований (см. Введение). Большинство существующих ВТ рассчитано на номинальную частоту 400 Гц, но может работать в диапазоне частот до 4000 Гц.

Конструкция.
    Вращающиеся трансформаторы в основном являются двухполюсными машинами. Однако в аналого-цифровых преобразователях «угол – код» и системах дистанционной передачи угла повышенной точности применяют и многополюсные вращающиеся трансформаторы, которые будут рассмотрены далее в § 4.3.
   Двухполюсные вращающиеся трансформаторы по конструкции и наличию скользящего контакта можно разделить на контактные и бесконтактные.

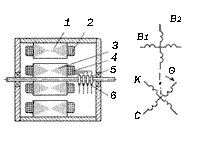
Рис 4.4 а,б

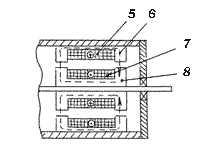
Рис 4.4 в

На рис. 4.4, а показана конструктивная схема контактного вращающегося трансформатора. Магнитопроводы статора 1 и ротора 3 собирают из листов электротехнической стали или пермаллоя, изолированных друг от друга лаком.
   В пазах магнитопроводов статора и ротора размещают по две распределенные обмотки, сдвинутые между собой на 90°. Обмотки статора 2 выполняют обычно одинаковыми, т.е. у них совпадает число витков, схема соединения витков и сечение обмоточного провода. Одинаковыми изготавливают и роторные обмотки 4. Пространственное расположение обмоток показано на рис. 4.4, б; В₁ – обмотка возбуждения, В₂ – квадратурная обмотка, С и К – синусная и косинусная обмотки. Возможны два варианта расположения обмоток: возбуждения и квадратурная (первичные) на статоре, синусная и косинусная (вторичные или выходные) на роторе; и наоборот. В дальнейшем при рассмотрении принципа работы и характеристик за основу принят первый вариант расположения обмоток.
   Выводы статорных обмоток подводят непосредственно к соединительным панелям, выводы роторных обмоток вращающихся трансформаторов контактного типа выводят через токосъемное устройство: четыре контактных кольца 5 и щетки 6.
   В бесконтактных вращающихся трансформаторах напряжения с обмоток ротора можно снимать (подавать) с помощью переходных кольцевых трансформаторов.
   В таком вращающемся трансформаторе на месте колец и щеток располагают переходные кольцевые трансформаторы. В общем случае их должно быть два, но при определенных схемах включения вращающихся трансформаторов удается обойтись одним переходным трансформатором. В двухобмоточном кольцевом трансформаторе (рис. 4.4, в) обмотки 5 и 7 расположены, соответственно, на кольцевых магнитопроводах 6 и 8.    Обмотки выполнены в виде сосредоточенных катушек, магнитные оси которых совпадают с направлением вала. Вследствие концентричного расположения при повороте ротора взаимоиндуктивность обмоток не меняется. При подаче на статорную обмотку кольцевого трансформатора переменного однофазного напряжения поток Ф_т наводит в его роторной обмотке неизменную по амплитуде вторичную ЭДС. Соединив проводами роторную обмотку кольцевого трансформатора с одной из основных роторных обмоток вращающегося трансформатора, можно подавать (или снимать) напряжение без колец и щеток. Длина бесконтактных вращающихся трансформаторов больше, чем контактных, в связи с необходимостью размещения переходных трансформаторов. Однако существенное повышение надежности окупает этот недостаток. Конструкция вращающихся трансформаторов и технология их изготовления должны обеспечивать при повороте ротора изменение взаимоиндуктивности М между обмотками статора и ротора по закону, наиболее близкому к идеальной синусоиде. Допустимое отклонение от идеального закона во многих случаях не должно превышать 0,005 %.

Синусно-косинусные ВТ. Принцип действия.
    Принцип работы вращающихся трансформаторов рассмотрим на примере получения синусной функции угла поворота ротора.

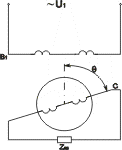
Рис 4.5 а

В этом режиме (рис. 4.5а) обмотка возбуждения В₁ присоединена к источнику переменного напряжения U₁. Выходная обмотка С подключена к внешней нагрузке, характеризуемой сопротивлением Z_нс =R_нс+jX_нс.    Квадратурная обмотка В₂ и выходная обмотка К разомкнуты и не принимают никакого участия в работе ВТ (на рис. 4.5 отсутствуют).
   Взаимоиндуктивность М_c между обмотками В₁ и С изменяется от угла поворота ротора Θ по закону

М_c= М_max sin Θ   (4.3)

где М_max – максимальная взаимоиндуктивность, соответствующая совпадению осей В₁ и С.
   Поскольку максимальная взаимоиндуктивность пропорциональна произведению чисел витков индуктивно связанных катушек, то уравнение (4.3) можно преобразовать

М_c= Λw_1эф.w_2эф.·sinΘ   (4.4)

где Λ-магнитная проводимость, значение которой не зависит от угла поворота вследствие равномерности воздушного зазора; w_1эф., w_2эф.- числа эффективных витков первичных и вторичных обмоток.

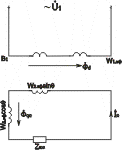
Рис 4.5 б

На основании уравнения (4.4) можно утверждать, что характер изменения взаимоиндуктивности Мс остается прежним, если число витков обмотки С рассматривать (рис. 4.5б) как геометрическую сумму “продольных витков” w_2эф.sin Θ, ось которых совпадает с осью обмотки В₁ и “поперечных витков” w_2эф.cosΘ, ось которых перпендикулярна оси обмотки В₁. Собственное сопротивление обмотки С, пропорциональное квадрату чисел витков, при этом также сохраняется неизменным, т.к. (w_2эф.sin Θ)2+(w_2эф.cosΘ)2=w_22эф.. Все это позволяет заменить схему рис. 4.5а эквивалентной схемой на рис. 4.5б.

1. Работа ВТ при холостом ходе (Z_нс = ∞ ; I_с = 0). ЭДС Ес обмотки С определяется только потоком взаимоиндукции между обмоткой В₁ и продольными витками w_2эф.sin Θ, т.е. только продольным потоком Ф_d. Тогда

Е_c/E_в1= w_2эф.sin Θ /w_1эф.   (4.5)

где E_в1 – ЭДС обмотки возбуждения; К_e=w_2эф./w_1эф. – коэффициент трансформации по ЭДС.
   Следовательно,

É_c=К_e É_в1·sinΘ   (4.6)

т.е. ЭДС обмотки С при холостом ходе ВТ в рассматриваемой схеме является синусоидальной функцией угла поворота ротора Θ.

2. Работа ВТ при нагрузке (Z_нс≠ ∞; I_с≠ 0). Продольный поток Ф_d создается совместным действием МДС обмотки возбуждения и МДС “продольных витков” синусной обмотки и примерно равен потоку в режиме холостого хода. Индуцируемая им в “продольных витках” ЭДС взаимоиндукции определяется как и в случае холостого хода

É_cM=К_e É_в1·sinΘ   (4.7)

Ток I_с, протекая по “поперечным виткам” w_2эф.sin Θ, создает поперечный поток Фqc, который не сцеплен с обмоткой возбуждения и значит не может быть скомпенсирован за счет увеличения тока в ней. Поток Ф_qc индуцирует в “поперечных витках” ЭДС самоиндукции

É_cL= -jωLÍ_c   (4.8)

где ω – угловая частота напряжения питания; L – индуктивность, пропорциональная квадрату числа витков и магнитной проводимости Λ:

L=(w_2эф.sin Θ)²Λ   (4.9)

Полная ЭДС, индуцируемая в обмотке С,

É_c= É_cM+É_cL    (4.10)

Ток ротора

Í_c= É_c/(Z_нс+Z_с)   (4.11)

где Z_с =R_с +jx_с- комплексное сопротивление синусной обмотки (R_с- активное сопротивление, x_с- индуктивное сопротивление рассеяния).
Подставляем (4.7) и (4.8) в (4.10) и с учетом (4.9) и (4.11) находим

É_c= К_e É_в1·sinΘ /(1+в·cos²Θ)   (4.12)

где в - комплексный множитель:

в = j·ωw²_2эф.Λ /(Z_нC+Z_C)   (4.13)

Из выражения (4.12) следует, что при нагрузке синусного ВТ происходит искажение синусоидального характера зависимости Ес от угла Θ (в знаменателе содержится в·cos²Θ), т.е. появляется погрешность отображения функциональной зависимости. Физически это искажение обусловлено появлением при нагрузке поперечного потока Ф_qc, т.е. поперечной реакцией выходной обмотки. Для уменьшения искажения необходимо уменьшить значение множителя в, что может быть достигнуто при больших значениях нагрузочного сопротивления. Поскольку множитель в является комплексным, то при изменении Θ изменяется и фаза выходной ЭДС.

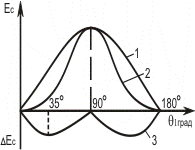
Рис 4.6

Погрешность отображения функциональной зависимости, вызванная реакцией, показана на рис. 4.6, где кривая 1- идеальная синусоида, кривая 2- выходная характеристика ВТ по (4.12) при в≠0, кривая 3 представляет собой зависимость погрешности ΔЕ_c от угла поворота ротора. Графически кривая 3 получается как разность кривых 1 и 2.
   Аналогичным образом можно рассуждать и в том случае, когда рабочей выходной обмоткой является обмотка К, а обмотка С разомкнута. При этом взаимоиндуктивность между обмотками В₁ и К изменяется по закону М_к=М_maxcos Θ и машина превращается в косинусный ВТ, для которого ЭДС при холостом ходе

É_к= К_e É_в1·sinΘ   (4.14)

и при нагрузке

É_к= К_e É_в1·sinΘ /(1+в·cos²Θ)   (4.15)

Симметрирование ВТ.
   Поскольку выходное напряжение вращающихся трансформаторов должно строго подчиняться закону синуса или косинуса угла поворота ротора, то приходится прибегать к так называемому симметрированию, т.е. устранению погрешности от поперечной реакции выходных обмоток путем компенсации этой реакции.

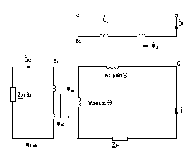
Рис 4.7 а

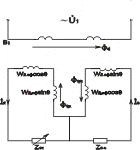
Рис 4.7 б

При первичном симметрировании вращающегося трансформатора используется квадратурная обмотка В₂, которая замыкается на внешнее сопротивление Z_внВ2. Витки этой обмотки на эквивалентной схеме (рис. 4.7а) и “поперечные витки” роторной обмотки С представляют собой трансформатор, первичной обмоткой которого является обмотка С, а вторичной – обмотка В₂. Ток I_с, протекая по “поперечным виткам” w_2эф.cosΘ обмотки С, создает магнитный поток Ф_В2, сцепленный с обмоткой В₂. В ней индуктируется трансформаторная ЭДС и течет ток I_В2. Значение результирующего поперечного потока Фq определяется геометрической суммой потоков Ф_В2 и Ф_qc обеих обмоток. При малом значении Z_внВ2 режим трансформатора близок к короткому замыканию и взаимное размагничивающее действие обеих обмоток настолько велико, что значение результирующего поперечного потока Фq стремится к нулю при любом значении сопротивления нагрузки Zнс. Можно доказать, что влияние поперечной реакции исчезает полностью, если включить в цепь обмотки В₂ сопротивление Z_внВ2= Z_внВ1, где Z_внВ1- внешнее сопротивление источника питания. Если ВТ подключен к выводам мощного источника питания, выходное сопротивление которого близко к нулю, то условием первичного симметрирования является Z_внВ2=0. Как видно, условие симметрирования от сопротивления нагрузки не зависит.
   Следует отметить, что при первичном симметрировании входное сопротивление вращающегося трансформатора зависит от угла поворота ротора. Это затрудняет применение ВТ с первичным симметрированием в многоступенчатых схемах.
   При вторичном симметрировании вращающегося трансформатора, обмотка С которого подключена к приемнику с входным сопротивлением Z_нс, включается соответствующее сопротивление Z_ик и в цепь второй выходной обмотки К. Из эквивалентной схемы (рис. 4.7б) видно, что токи I_c и I_к, протекая по “поперечным виткам” w_2эф.sinΘ, создают поперечные потоки Ф_qc и Ф_qк, направленные в противоположенные стороны, т.е. взаимно ослабляющие друг друга. Для полной компенсации поперечного потока (Ф_q=0) необходимо равенство поперечных потоков Ф_qc и Ф_qк, т.е. должно соблюдаться равенство ЭДС “поперечных витков” I_cw_2эф.cos Θ=I_кw_2эф.sin Θ.
   Нетрудно доказать, что это равенство справедливо только при

Z_нс + Z_с= Z_нк + Z_к   (4.16)

Выражение (4.16) является условием полной компенсации поперечной реакции при вторичном симметрировании вращающегося трансформатора. При выполнении условия вторичного симметрирования входное сопротивление вращающегося трансформатора не зависит от угла поворота ротора.
   Применение вторичного симметрирования затрудняется при переменной нагрузке вращающегося трансформатора, так как ее значение входит в условие симметрирования (4.16). Наименьшая степень искажения выходных характеристик синусно-косинусного вращающегося трансформатора достигается при совместном применении первичного и вторичного симметрирования.
   Итак, при выполнении условий симметрирования ЭДС выходных обмоток и при нагрузке будут изменяться строго по закону синуса и косинуса от угла поворота ротора Θ. Очевидно, по этому же закону будут изменяться и выходные напряжения; максимальное значение этих напряжений зависит от значения и характера нагрузочного сопротивления. Коэффициент трансформации ВТ по напряжению К_u, равный отношению наибольшего выходного напряжения к напряжению возбуждения, несколько отличается от отношения чисел витков К_c. Фаза выходного напряжения симметричного СКВТ отличается от фазы напряжения возбуждения U₁ на угол φ и дискретно меняется на 180° через 180° угла поворота ротора. При соблюдении условия симметрирования выходные напряжения на основании (4.5) и (4.6) можно записать в виде

Ú_c= К_uÚ₁sin Θ, Ú_к= К_u Ú₁cos Θ, (4.17)

где коэффициент трансформации по напряжению в комплексной форме К_u= К_uе^jφ.
   Точный расчет значения и фазы выходного напряжения может быть выполнен по эквивалентным схемам.

Погрешности и классы точности ВТ.
    Принципиальные погрешности СКВТ – это отклонение выходных характеристик от синусоидальной и косинусоидальной вследствие неточности симметрирования (см.(4.12)); у линейных – отклонение выходной характеристики от линейной вследствие неточности аппроксимации.
   Конструктивные погрешности вызываются в основном несинусоидальностью распределения МДС обмоток вдоль окружности машины, изменением магнитного сопротивления воздушного зазора вследствие наличия пазов на поверхности статора и ротора, нелинейностью кривой намагничивания и явлением гистерезиса. Уменьшение этих погрешностей достигается путем применения специальных “ синусных” схем обмоток, за счет скоса пазов статора и ротора, выполнения магнитопровода ВТ ненасыщенным из пермаллоя с узкой петлей намагничивания.
   Основными источниками технологических погрешностей являются эксцетриситет расточек статора и ротора, асимметрия магнитопровода, неточность расположения и скоса пазов, наличие короткозамкнутых витков в обмотках и листов в магнитопроводе, ошибки при выполнении обмотки. Для уменьшения этих погрешностей устанавливаются жесткие технологические допуски.
   Влияние технологических погрешностей можно представить как появление некоторой добавочной ЭДС Е_доб в выходных обмотках. ЭДС Едоб имеет в общем случае две составляющие: ЭДС (напряжение) ошибки Еош, совпадающую по фазе с выходной ЭДС, и остаточную ЭДС Еост, сдвинутую по фазе на 90°. При этом в расчетных точках с нулевым выходным напряжением (нулевых положениях) ЭДС становится отличной от нуля. ЭДС ошибки Еош может быть скомпенсирована основной выходной ЭДС путем дополнительного поворота ротора на угол, при котором Е_вых= -Е_ош, т.е. обуславливает асимметрию нулевых положений.
   Остаточная ЭДС Е_ост не компенсируется дополнительным поворотом ротора. Поэтому во вращающихся трансформаторах выходное напряжение не обращается в нуль в пределах оборота, а лишь приобретает некоторое минимальное значение. Остаточная ЭДС приводит к изменению фазы выходной ЭДС при изменении угла поворота ротора.
   Технологические погрешности приводят также к тому, что поток возбуждения наводит ЭДС в квадратурной обмотке ВТ.
   К эксплуатационным погрешностям относятся, например, температурная погрешность, связанная с изменением активных сопротивлений обмоток при изменении температуры. Колебание частоты напряжения питания вызывает изменение индуктивных сопротивлений.
   Класс точности вращающихся трансформаторов устанавливается для нормальных условий эксплуатации. При определении класса точности учитываются следующие показатели:
   1) погрешность отображения функциональной зависимости, определяемая по отношению к наибольшей выходной ЭДС; у СКВТ различных классов погрешность допускается от 0.005 до 0,2 %, у ЛВТ – от 0,02 до 0,2 %.
   2) асимметрия нулевых положений ротора ВТ, под которой понимается отклонение действительных нулевых положений ротора от теоретических 0°, 90°, 180° и 270°; у СКВТ различных классов асимметрия допускается от 10’’ до 6’ 40’’;
   3) ЭДС квадратурной обмотки, определяемая по отношению к напряжению возбуждения; у СКВТ различных классов допускается от 0,04 до 1,2%;
   4) остаточная ЭДС, определяемая по отношению к наибольшей выходной ЭДС; у СКВТ различных классов допускается от 0,03 до 0,1 %; у ЛВТ – от 0,02 до 0,3 %;
   5) разность коэффициентов трансформации выходных обмоток, определяемая по отношению к наибольшему из этих коэффициентов; у СКВТ различных классов допускается от 0,005 до 0,2 %.
   Класс точности устанавливается по наихудшему из параметров.
В заключении следует отметить, что в данном параграфе были рассмотрены только статические характеристики ВТ, поскольку в динамическом отношении в подавляющем большинстве случаев их можно считать усилительными звеньями.