§2.3. Асинхронный двигатель как обобщенный трансформатор

Можно показать, что физические процессы в асинхронном двигателе имеют много общего с процессами в трансформаторе, и асинхронный двигатель можно анализировать на основе системы уравнений и схемы замещения, полученных для трансформатора.
   Как и в трансформаторе, в двигателе имеется основной магнитный поток Ф₀, сцепленный с проводниками статора (первичной обмоткой) и ротора (вторичной обмоткой). Этот поток вращается c угловой скоростью ω₁ = 2πf /р_м, т.е. изменяется с частотой напряжения питания f₁. При этом в обмотках статора и ротора наводятся ЭДС взаимоиндукции e₁ и e₂.
   При замкнутой обмотке ротора поток Ф₀ создается в результате взаимодействия МДС статора и ротора, неподвижных друг относительно друга. Действительно, частота тока в обмотке ротора прямо пропорциональна разности угловых скоростей поля и ротора и числу пар полюсов, т.е.

f₂= (ω₁ - ω₂)p_м /2π   (2.9)

Обмотка ротора является многофазной, и токи ротора создают МДС, вращающуюся относительно ротора с угловой скоростью ω₂₂ = 2πf₂ /р_м = ω₁ -ω₂. Угловая скорость этой МДС относительно статора ω₂₁ =ω₂ +ω₂₂ = ω₁, т.е. МДС статора и ротора вращаются относительно статора с одной угловой скоростью. Воздействие МДС ротора на магнитное поде двигателя называется реакцией ротора. В асинхронных двигателях реакция ротора проявляется так же, как реакция вторичной обмотки в трансформаторах.
   МДС обмоток статора и ротора создают потоки рассеяния, сцепленные каждый со своей обмоткой и наводящие ЭДС самоиндукции е_σ1 и е_σ2.

Наряду с этими общими чертами, у асинхронного двигателя имеется и ряд отличий.
    1. При уменьшении угловой скорости ротора ω₂ увеличивается частота перемагничивания магнитопровода ротора и, соответственно, магнитные потери мощности в роторе на гистерезис и вихревые токи. Однако примерно в этой же пропорции уменьшаются механические потери на трение в подшипниках. В результате в двигателе можно условно выделить переменные, зависящие от нагрузки потери мощности - электрические потери ΔР_э в обмотках, и постоянные потери - сумму магнитных ΔР_м и механических ΔР_мех. потерь.
   2. Согласно (2.9) и (2.8) частота токов в роторе

f₂ = s·f₁,   (2.10)

т.е. она зависит от угловой скорости ротора и в двигательном диапазоне изменяется от f₂ = f₁ до f₂ = 0. Это делает невозможным прямое использование векторных диаграмм и схем замещения трансформатора для анализа асинхронного двигателя.
   Поступаем следующим образом.Выразим параметры вращающегося ротора через параметры неподвижного ротора ( s = 1 ), для которого согласно (2.10) f₂ = f₁ = const.
   Выражение ЭДС обмотки фазы вращающегося ротора, записанное по аналогии с (1.7),

Е_2вр = 4,44 f₂ Ф_м w_2эф = 4,44 s f₁ Ф_м w_2эф =s E₂   (2.11)

где ЭДС при неподвижном роторе

E₂ = 4,44 f₁Ф_м w_2эф   (2.12)

Ф_м - амплитуда потока Ф₀ , w_2эф - число эффективных витков обмотки фазы ротора.
   Индуктивное сопротивление ротора

x _2вр = 2πf₂·L_σ2 = s·x₂   (2.13)

где x _2вр = 2πf₂·L_σ2 - индуктивное сопротивление обмотки фазы неподвижного ротора; L_σ2 - индуктивность рассеяния.
   Пренебрегая поверхностным эффектом будем считать, что R₂ =const.
Ток во вращающемся роторе по закону Ома

I_2вр= E_2вр /√(R₂²- x_2вр²)   (2.14)

С учетом (2.11) и (2.13) формула (2.14) преобразуется следующим образом

I_2вр= sE₂ /√(R₂²+sx₂²) = E₂ /√((R₂/s) ²+x₂²)   (2.15)

Как видно, ток ротора определен непосредственно через параметры неподвижного ротора и имеет частоту ЭДС неподвижного ротора. Поэтому индекс "вр" у тока ротора в дальнейшем опускается.
   Фаза тока ротора, характеризуемая углом ψ₂ между E_2вр и I₂,может
быть определена из выражения (2.16).

cos ψ₂ = R₂ /√(R₂²+(sx₂)²)    (2.16)

3. У двигателя нагрузка механическая, а у трансформатора - электрическая. Для учета этого различия представим активное сопротивление R₂ /s в (2.15) как сумму R₂ +R₂(1-s) /s. Тогда R₂ соответствует электрическим потерям в обмотке ротора, а R₂(1-s) /s соответствует электрической мощности, преобразуемой в механическую. Поскольку s зависит от момента нагрузки, то сопротивление R₂(1-s) /s является эквивалентом механической нагрузки двигателя. Изменение этого сопротивления так же влияет на токи в обмотках и потребляемую мощность, как и изменение момента нагрузки на валу вращающегося ротора. Таким образом, короткозамкнутая обмотка вращающегося ротора асинхронного двигателя подобна вторичной обмотке трансформатора, включенной на условное сопротивление нагрузки:

R_ну = R₂(1-s) /s   (2.17)

Следовательно, асинхронный двигатель можно рассматривать как обобщенный трансформатор, у которого сопротивление R_ну является эквивалентом механической нагрузки двигателя.
   Как видно из (2.15), в двигательном диапазоне наибольший ток в роторе будет при пуске ( s=1). При идеальном холостом ходе двигателя, т.е. при s=0, ток I₂ = 0.

Схема замещения.
   Схема замещения строится для приведенного асинхронного двигателя, у которого число фаз, расположение обмоток фаз и число витков в обмотке фазы ротора такие же, как на статоре. Приведение параметров ротора к числу фаз и витков обмотки статора осуществляется, как и у трансформатора, исходя из условия инвариантности мощности. Нетрудно показать, что формулы приведения для двигателя примут вид:

E₂' = K_eE₂; I₂' = I₂ /K_i ; Х₂' = K_e K_i X₂; R₂' = K_e K_i R₂   (2.18)

где Ke = w_1эф / w_2эф – коэффицент трансформации ЭДС;
    K_i = m₁ w_1эф / m₂ w_2эф – коэффицeнт трансформации тока;
    m₁ и m₂ - число фаз статора и ротора.

В соответствии с выводами, сделанными в предыдущем разделе настоящего параграфа, в качестве схемы замещения приведенного асинхронного двигателя (в расчете на одну фазу) может использоваться схема замещения однофазного трансформатора (см. рис. 1.6) с заменой сопротивления ветви нагрузки на условное сопротивления R_ну по (2.17). Получающаяся схема замещения двигателя изображена на рис. 2.10.

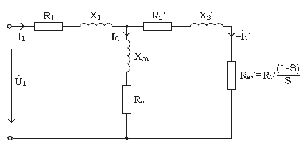
Рис. 2.10

Назад | Оглавление | Вперед