Содержание
< назад вперед >
§ 78. СОЕДИНЕНИЕ ЗВЕЗДОЙ
Если фазные
обмотки генератора или потребителя соединить так, чтобы концы обмоток были
соединены в одну общую точку, а начала обмоток присоединены к линейным
проводам, то такое соединение
называется соединением звездой и обозначается условным
знаком Y. На рис. 173 обмотки
генератора и потребителя соединены
звездой. Точки, в которых соединены концы фазных обмоток
генератора или потребителя, называются соответственно нулевыми точками генератора (0) и потребителя
(0'). Обе точки 0 и 0' соединены проводом, который называется
нулевым, или нейтральным, проводом. Остальные
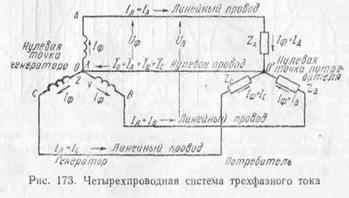
три провода
трехфазной системы, идущие от генератора к потребителю,
называются линейными проводами. Таким
образом, генератор соединен с потребителем четырьмя проводами. Поэтому эта система
называется четырех проводной системой трехфазного тока.
Сравнивая
несвязанную (см. рис. 172) и четырехпроходную
(см. рис. 173) системы
трехфазного тока, видим, что в первом случае
роль обратного провода выполняют три провода системы, а во втором
— один нулевой провод. По нулевому проводу протекает ток, равный геометрической
сумме трех токов:
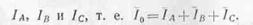
Напряжения, измеренные между
началами фаз генератора (или потребителя)
и нулевой точкой (или нулевым проводом), называются фазными напряжениями и
обозначаются Uа, Uв, Uс, или в общем виде Uф. Часто задаются величины э.
д. с. фазных обмоток генератора. Они обозначаются ЕА, Ев, Ее, или Еф. Если пренебречь
сопротивлениями обмоток генератора, то можно записать:
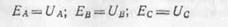
Напряжения, измеренные между началами двух фаз: А и В, В и С, С и А —
генератора или потребителя, называются линейными
напряжениями
и обозначаются Uab, Uвс, Uса, или в общем
виде Uл. Стрелки, поставленные на
рис. 173, показывают
выбранное положительное направление тока, которое в линейных
проводах принято от генератора к потребителю, а в нулевом проводе — от потребителя к
генератору.
Если
присоединить зажимы вольтметра к точкам А и В, то он покажет
линейное напряжение Uав. Так как положительные
направления фазных напряжений Ua, Uв и Uс выбраны от начал
фазных обмоток к их концам, то вектор линейного напряжения UАВ будет равен
геометрической разности векторов
фазных напряжений UA и UB:
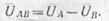
Аналогично можно записать:
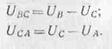
Иначе можно сказать, что
мгновенное значение линейного напряжения равно разности мгновенных значений
соответствующих фазных напряжений.
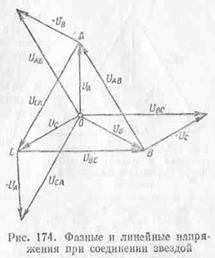
На рис. 174 вычитание
векторов заменено сложением векторов:
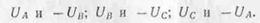
Из векторной
диаграммы видно, что векторы линейных напряжений составляют замкнутый
треугольник.
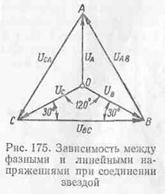
Зависимость между линейным и
фазным напряжениями показана на рис. 175:
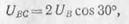
так как
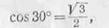
то
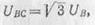
или в общем
виде
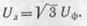
Следовательно,
при соединении звездой линейное напряжение в 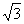 раз больше
фазного напряжения. раз больше
фазного напряжения.
В
дальнейшем, говоря о напряжении в цепях трехфазного переменного
тока, если не будет сделано оговорок, будем иметь в виду линейное напряжение.
Ток, протекающий по фазной
обмотке генератора или потребителя, называется фазным током и обозначается в общем виде Iф. Ток,
протекающий по линейному проводу,
называется
линейным током и обозначается
в общем виде Iл.
На рис. 173
видно, что при соединении звездой линейный ток
равен фазному току, т. е. Iл =Iф.
Рассмотрим
случай, когда нагрузка в фазах
потребителя одинакова как по величине, так и по характеру.
Такая нагрузка называется равно мерной, или симметричной. Это условие выражается равенством
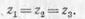
Нагрузка не
будет равномерной, если, например, z1 = r1 = 5 ом; z2 = wL2 =5 ом и z3 = 1/(wC3) = 5 ом, так как здесь выполнено лишь одно условие — равенство сопротивлений
фаз потребителя по величине, в то время как характер сопротивлений различен (r1 — активное сопротивление, х2 = wL2 —
индуктивное сопротивление, 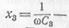 емкостное
сопротивление). емкостное
сопротивление).
При симметричной нагрузке
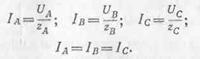
Фазные коэффициенты мощности
вследствие равенства сопротивлений и одинаковости их характера будут
одинаковы:
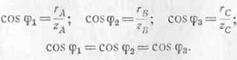
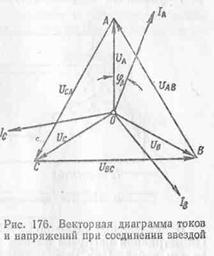
На рис. 176 дана векторная
диаграмма напряжений и токов при симметричной нагрузке,
соединенной звездой.
Нам уже
известно, что в нулевом проводе должна протекать геометрическая
сумма токов всех трех фаз. На рис. 177 даны кривые
изменения токов при симметричной нагрузке трехфазной системы. Так
как нагрузка симметрична, то максимальные значения для всех трех синусоид тока
одинаковы.
Рассмотрим момент а. Чтобы
получить ток в нулевом проводе, сложим мгновенные значения
токов всех трех фаз. В этот момент ток третьей фазы i3 равен нулю. Мгновенное
значение тока в первой фазе равно
i1, причем этот
ток направлен в одну сторону. Одновременно ток во второй фазе
равен i2, но этот ток направлен в
обратную сторону. Так как ток i1 равен току
i2, но оба
они имеют противоположные направления, а
ток 13 равен нулю, то сумма всех
токов также равна нулю.
Сумма трех токов будет равна нулю также в момент в.
В момент б ток первой
фазы имеет максимальное положительное
значение i1. В то же
время токи второй и третьей фаз i2 и i3, которые равны между собой,
имея отрицательное направление, в сумме равны току i1. Поэтому
сумма трех токов снова равна нулю.
При
рассмотрении любых других моментов мы также увидим, что при
симметричной нагрузке сумма мгновенных значений токов трехфазной
системы равна нулю. Следовательно, ток в нулевом про-
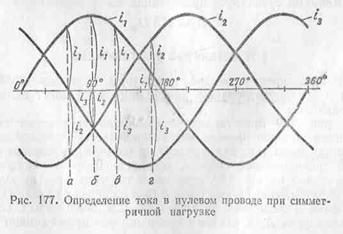
воде будет равен нулю.
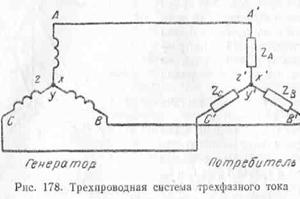
Отбрасывая нулевой провод в четырехпроводной
системе, переходим к трехпроводной системе трехфазного тока,
которая представлена схематически на рис. 178. Таким образом, если имеется
симметричная нагрузка, как, например, трехфаз  ные двигатели переменного тока, трехфазные
печи, трехфазные трансформаторы и т. п., то к
такой нагрузке подводятся только три провода. ные двигатели переменного тока, трехфазные
печи, трехфазные трансформаторы и т. п., то к
такой нагрузке подводятся только три провода.
Потребители, включенные
звездой с несимметричной нагрузкой фаз, нуждаются в нулевом
проводе.
В заключение необходимо
обратить внимание на то, что при Симметричной
нагрузке фазные напряжения отдельных фаз равны между собой. При несимметричной
нагрузке трехфазной системы симметрия
токов и напряжений нарушается. Однако в четырехпроводных цепях часто
пренебрегают незначительной несимметрией фазных
напряжений. В этих случаях между линейными и фазными напряжениями существует
приведенная выше зависимость
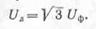
| 
