<< Предыдущая |
Содержание |
Следующая >>
Цепь переменного тока с параллельно соединенными сопротивлениями
§ 57. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С
ПАРАЛЛЕЛЬНО СОЕДИНЕННЫМИ СОПРОТИВЛЕНИЯМИ
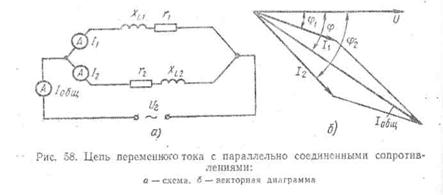
На рис. 58 изображена цепь переменного тока, в которую
включены параллельно две катушки. Каждая из этих катушек обладает
соответственно активным сопротивлением
r1 и
r2 и
индуктивным сопротивлением XL1 и XL2.
Полное сопротивление первой
катушки
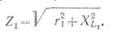
Полное сопротивление второй
катушки
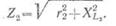
Напряжение на зажимах
катушек равно напряжению генератора.
Сила тока в каждой катушке
определяется согласно закону Ома:
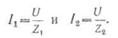
Из этих равенств можно
сделать вывод, что в такой цепи токи разветвляются обратно пропорционально
полным сопротивлениям ветвей.
Для определения угла сдвига
фаз между напряжением и током
в каждой катушке вычисляют 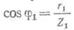 и и 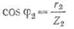 и по таблице тригонометрических
функций находят значения углов
j1 и
j2. и по таблице тригонометрических
функций находят значения углов
j1 и
j2.
Чем больше угол сдвига фаз
между напряжением и током, тем больше реактивный ток и меньше активный, тем
хуже используется электрический ток в данной установке, ниже ее коэффициент мощности
(cos
j).
Так как первый закон Кирхгофа
справедлив для цепей переменного тока, то в рассматриваемой цепи общий ток
определяется геометрическим сложением векторов (рис. 58,6).
По горизонтали в выбранном
масштабе отложим вектор напряжения
U. Так
как ток в цепи с индуктивностью отстает от напряжения, то вектор тока I1 выбранном масштабе отложим с помощью транспортира
под углом j1 к вектору напряжения
U, а вектор тока
I2 и
отложим под углом j2. Общий
ток в цепи будет равен сумме векторов тока
I1 и
I2, который
определяется с учетом выбранного масштаба.
Чтобы найти общий ток, нужно
воспользоваться тем, что активная составляющая общего тока — общий активный
ток равен сумме активных токов ветвей:
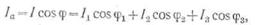
а общий реактивный ток —
сумме реактивных токов ветвей (если все эти реактивные токи, отстающие по фазе
или все опережающие):
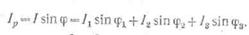
После чего определяют общий ток:

Угол сдвига фаз между общим
током и напряжением ср находят по векторной диаграмме.
Пример. Три
катушки соединены параллельно и к ним подключено переменное напряжение
U=100 в. Частота тока 50 гц.
Активное сопротивление катушки r1=2
ом; r2=3 ом;
r3=4 ом;
Индуктивность катушек L1=0,04 гн;
L2=0,03 гн; L3=0, 01 гн.
Вычислить силу тока в каждой катушке и общий ток в цепи, а
также угол сдвига фаз между током и напряжением.
Решение. Индуктивное сопротивление катушек:

Полное сопротивление катушек:
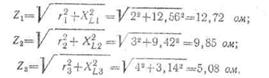
Сила
тока в катушках:
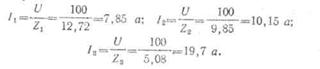
Общий ток в цепи равен
векторной сумме токов.
Для определения угла сдвига
фаз между током и напряжением каждой ветви вычисляют:
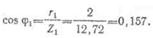
По таблице тригонометрических функций находят, что если
cos j1=0,157,
то угол сдвига фаз в первой ветви j1=80055’; если
cos j2=0,305,
то угол сдвига фаз j2=72015’;
если cos j3=0,79,
то угол сдвига фаз j3=37050’;
Зная угол сдвига фаз между током и напряжением для каждой
ветви, построим векторную диаграмму токов и напряжения и определим по ней общую
силу тока в цепи.
 Для
этого отложим по горизонтали в выбранном
масштабе вектор напряжения U. Для
этого отложим по горизонтали в выбранном
масштабе вектор напряжения U.
Под углом j1=80°66'
с помощью транспортира отложим
вектор тока I1=7,85 а. Под углом
j2=72°15'
(к горизонтали) отложим вектор
I2=
10,15 а как продолжение вектора I1. Под углом j3=37°50'
(к Горизонтали) отложим вектор I3=
19,7 а как продолжение вектора I2. Общий ток равен
длине вектора I
с учетом выбранного масштаба, который соединяет начало
вектора I1
и конец вектора I3. Для нашего примера он равен 36,5 а. Общий угол
сдвига фаз между током I и напряжением U измеряют с помощью транспортира, он равен 56°.
<< Предыдущая |
Содержание |
Следующая >>
| 
