Второй закон Киргофа

§ 21. ВТОРОЙ ЗАКОН КИРХГОФА

Второй закон Кирхгофа может быть сформулирован следующим образом: во всякой замкнутой электрической цепи алгебраическая сумма всех э. д. с. равна алгебраической сумме падений напряже­ния в сопротивлениях, включенных последовательно в эту цепь, т. е.

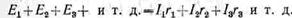
Если в электрической цепи включены два источника энергии, э. д. с. которых совпадают по направлению, т. е. согласно (рис. 20, а), то э. д. с. всей цепи равна сумме э. д. с. этих источников, т. е.

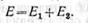
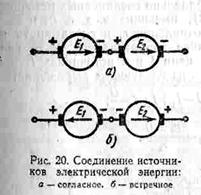
Если же в цепь включено два источника, э. д. с. которых имеют противоположные направления, т. е. включены встречно (рис. 20,6), то  общая   э. д. с.   цепи   равна   разности   э. д. с.   этих   источников,

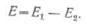
При последовательном включении в электрическую цепь не­скольких источников энергии с различным направлением э. д. с. общая э. д. с. равна алгебраической сумме э. д. с. всех источников. Суммирование э. д. с. одного направления берут со знаком плюс, а э. д. с. противоположного направления — со знаком минус. При составлении уравнений выбирают направление обхода цепи и про­извольно задаются направлениями токов.

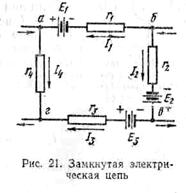
Обычно замкнутая цепь является частью сложной цепи, как показано, например, на рис. 21. Замкнутая цепь обозначена буква­ми а, б, в и г. Ввиду наличия ответвлений в точках а, б, в, г токи I₁, I₂, I₃  и I₄, отличаясь по силе, могут иметь и различные направле­ния. Для такой цепи в соответствии со вторым законом Кирхгофа можно написать:

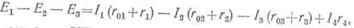
где r₀₁, r₀₂, r₀₃  — внутренние сопротивления источников энергии,

      r₁, r₂, r₃ — сопротивления приемников энергии.

В частном случае при отсутствии ответвлений и последователь­ном   соединении  проводников   общее  сопротивление равно сумме всех сопротивлений.

Если внешняя цепь источника энергии с внутренним сопротив­лением r₀ состоит, например, из трех последовательно соединенных резисторов с сопротивлениями, соответственно равными r₁, r₂, r₃, то на основании второго закона Кирхгофа можно написать следующее равенство:

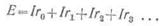
При  нескольких  источниках  тока   в левой части этого равенства была бы алгебраическая сумма

э. д. с. этих источников.

При параллельном включении двух или не­скольких источников энергии токи, протекающие в них, в общем случае неодинаковы.

Если два параллельно соединенных источника энергии (рис. 22), имеющих э. д. с. Е₁ и Е₂ и внутренние сопротивления r₁ и r₂,. замкнуть на какое-либо внешнее сопротивление r, то силу тока во внешней цепи I и в источниках I₁ и I₂ можно определить из следующих выражений:

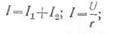
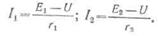
Отсюда сила тока во внешней цепи

Сила тока, протекающего через первый и второй источники энер­гии,:

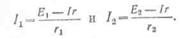
Пример 1.   В схеме, изображенной на рис. 21, э. д. с. источников энергии и сопротивления  приемников энергии имеют следующие значения: Е₁=6 в, Е₂=12 в, Е₃=9 в, r₁=8 ом, r₂=5 ом, r₃=4 ом и r₄=10 ом.
Решение. Алгебраическая сумма э.д.с. в цепи

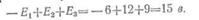
В этом выражении э. д. с. Е₁ взята со знаком минус потому, что первый источник энергии включен встречно второму и третьему.

Общее сопротивление цепи

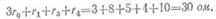
Сила тока в цепи

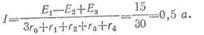
Напряжение между точками а и г

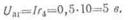
Пример 2. Два параллельно соединенных генератора (см. рис. 22), имеющие э. д. с. Е₁=Е₂=120 в и внутренние сопротивления r₁=3 ом и r₂=6 ом, замкнуты на сопротивление r=18 ом.

Определить силу тока во внешней цепи и токи в первом и во втором гене­раторах.

Решение. Внутреннее сопротивление двух параллельно соединенных гене­раторов.

Сила тока во внешней  цепи

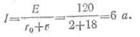
Токи в первом и во втором генераторах обратно пропорциональны внутрен­ним сопротивлениям этих генераторов, т. е.

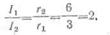
Таким образом, I₁ + I₂ =3I₂ = 6 a,  откуда  I₂  = 2 a, I₁  = 2I₂  = 4 a.