|
Министерство общего и профессионального образования
Российской Федерации
Санкт-Петербургский государственный институт точной
механики и оптики
(технический университет)
Кафедра электротехники
и прецизионных электромеханических систем
Усольцев А.А.
ВЕКТОРНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ
Учебное пособие
по дисциплинам электромеханического цикла
Санкт-Петербург
2002

Содержание
Развитие асинхронного электропривода с векторным управлением
1. ВЕКТОРНАЯ МОДЕЛЬ АСИНХРОННОГО ДВИГАТЕЛЯ
1.1. Понятие обобщенного вектора
1.2. Основные соотношения между токами и потокосцеплениями АД
1.3. Индуктивность составляющей нулевой последовательности
1.4. Уравнения статора и ротора в векторной форме
1.5. Обобщённая электрическая машина
1.5.1. Электромагнитный момент АД
1.6. Модель короткозамкнутого АД при частотном управлении
2. ВЕКТОРНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ
2.1. Общий принцип векторного управления АД
2.2. Модель АД, управляемого током статора, в системе координат, ориентированной по потокосцеплению ротора
2.3. Модель АД, управляемого напряжением статора, в системе координат, ориентированной по потокосцеплению ротора
2.4. Основные элементы систем векторного управления АД
2.4.1. Усилитель мощности релейного типа
2.4.2. Преобразователи числа фаз
2.4.3. Вектор-анализаторы и ротатор
2.5. Замкнутые системы векторного управления АД
2.5.1. Характеристики системы с П-регулятором скорости
2.5.2. Характеристики системы с ПИ-регулятором скорости
Список литературы

Развитие асинхронного электропривода с векторным управлением.
Современные
системы векторного управления прошли долгий путь развития и в настоящее
время являются наиболее распространенными среди систем электропривода
переменного тока. Они позволяют просто и эффективно управлять такими
сложными объектами как асинхронный двигатель с короткозамкнутым ротором
(АД), что в свою очередь, позволяет существенно расширить область его
применения, почти полностью вытесняя из автоматизированных управляемых
приводов двигатели постоянного тока. Это связано в первую очередь с
развитием силовой электроники, позволяющей создавать надежные и
относительно дешевые преобразователи, а также с развитием
быстродействующей микроэлектроники, способной реализовать алгоритмы
управления практически любой сложности. Поэтому высококачественный
асинхронный векторный электропривод (АВП) в настоящее время является по
существу техническим стандартом.
Первым этапом
процесса развития АВП была разработка универсальной векторно-матричной
математической модели, получившей название обобщенной электрической
машины, которая началась в конце 20-х годов и завершилась в конце 40-х
годов ХХ века. Эта модель позволяет описывать электромагнитные процессы в
идеализированной электрической машине с помощью аппарата линейной
алгебры. Практическое использование модели было отложено на несколько
десятилетий, т.к. при ручных расчетах она не давала каких-либо
преимуществ, но требовала существенных вычислительных затрат,
теоретически же ее успешно использовали для анализа переходных процессов
в электрических машинах.
В 1971 году F. Blaschke
предложил принцип построения системы управления асинхронным двигателем,
в котором использовалась векторная модель АД с ориентацией системы
координат по потокосцеплению ротора. Сущность предложенного метода,
получившего впоследствии название векторного, заключалась в
использовании в системе управления передаточных функций обратных по
отношению к передаточным функциям векторной модели АД, что позволяло
получить в качестве независимых входных переменных системы величины,
входящие в уравнение электромагнитного момента. Поэтому этот принцип
называется также прямым управлением моментом. Кроме того, для упрощения
задачи в векторной модели АД использовалась система координат,
ориентированная по одному из векторов, входящих в уравнение
электромагнитного момента, что существенно упрощало передаточные функции
системы и позволяло определить момент двумя независимыми переменными
аналогично тому, как это делается в двигателях постоянного тока.
За три
прошедшие десятилетия были разработаны десятки вариантов исходных
моделей АВП, реализованы сотни устройств на разной элементной базе,
опубликованы тысячи статей и монографий, но принцип и первая модель,
предложенная F. Blaschke, по-прежнему доминируют в технических реализациях.

1.1. Понятие обобщенного вектора.
Большинство
электрических машин переменного тока предназначено для работы в
трехфазных сетях, поэтому они строятся с симметричными трехфазными
обмотками на статоре, причем МДС этих обмоток распределены в
пространстве по закону близкому к синусоидальному, т.е. МДС, создаваемая
k-й обмоткой в точке, отстоящей от оси этой обмотке на угол a k равна –Fa k=Fk0cosa k, где Fk0 – МДС, соответствующая оси k-й обмотки. Синусоидальность
распределения позволяет представить МДС или пропорциональные им токи
обобщенным пространственным вектором на комплексной плоскости,
т.е. вектором, представляющим собой геометрическую сумму отрезков,
построенных на пространственных осях фазных обмоток и соответствующих
мгновенным значениям фазных МДС или токов. При этом проекции обобщенного
вектора на оси фазных обмоток в любой момент времени будут
соответствовать мгновенным значениям соответствующих величин.
При симметричной трехфазной системе обмоток обобщенный вектор тока можно представить в виде
|
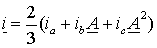
|
(1.1.1) |
где 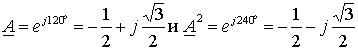 – операторы поворота, а ia, ib и ic
– мгновенные значения токов соответствующих обмоток. Обозначение
вектора строчным символом принято для указания на то, что его координаты
являются функциями времени аналогично тому, как строчные символы при
обозначении скалярных величин указывают на мгновенное значение. – операторы поворота, а ia, ib и ic
– мгновенные значения токов соответствующих обмоток. Обозначение
вектора строчным символом принято для указания на то, что его координаты
являются функциями времени аналогично тому, как строчные символы при
обозначении скалярных величин указывают на мгновенное значение. 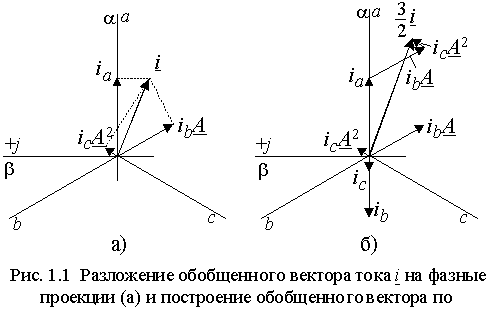
При таком представлении фазные токи ia, ib и ic можно рассматривать как проекции вектора i на соответствующие оси фазных обмоток (рис. 1.1 а)). Если произвести построение вектора i , откладывая значения фазных токов ia, ib и ic
на осях обмоток (рис. 1.1 б)), то суммарный вектор окажется в полтора
раза больше того вектора, проекции которого соответствуют фазным токам.
Поэтому в выражении (1.1.1)
присутствует коэффициент 2/3, приводящий модуль суммарного вектора к
такому значению, которое при проецировании на оси фазных обмоток даст
истинные значения фазных токов.
Если статор
машины имеет нулевой провод, то фазные токи могут содержать нулевую
составляющую и их значения можно представить в виде ia+io, ib+io и ic+io. Тогда вектор тока будет равен
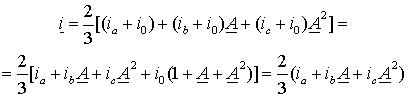
Таким образом, обобщенный вектор тока статора не содержит нулевой составляющей и ее при анализе следует учитывать особо.
Обобщенный
вектор, как и любой вектор на комплексной плоскости, можно представить
алгебраической формой записи комплексного числа. Обычно это делают,
совмещая вещественную ось с осью обмотки a (рис. 1.1), тогда
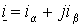 . .
Подставляя в выражение (1.1.1) значения операторов поворота, записанные в алгебраической форме, и разделяя вещественную и мнимую части получим
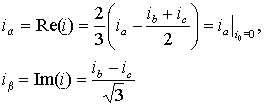
Если фазные токи содержат нулевую составляющую, то ее значение будет равно 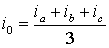 .
Переход от представления обобщенного вектора через проекции на оси
трехфазных обмоток к представлению через проекции на оси комплексной
плоскости эквивалентно преобразованию трехфазной системы обмоток в
эквивалентную двухфазную. В матричной форме это преобразование можно
записать в виде .
Переход от представления обобщенного вектора через проекции на оси
трехфазных обмоток к представлению через проекции на оси комплексной
плоскости эквивалентно преобразованию трехфазной системы обмоток в
эквивалентную двухфазную. В матричной форме это преобразование можно
записать в виде
|
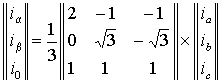 . .
|
(1.1.2) |
Отсюда обратное преобразование координат обобщенного вектора –
|
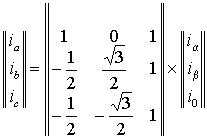
|
(1.1.3) |
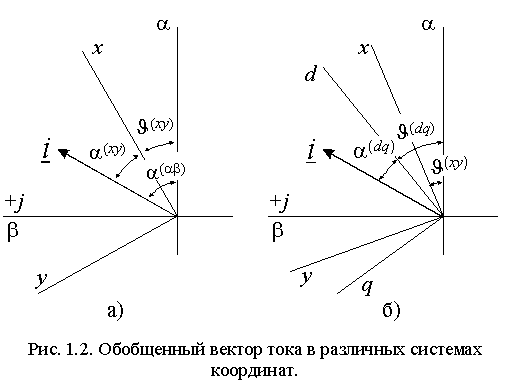
Обобщенный
вектор можно представить также во вращающейся системе координат. Если
вектор тока представлен в неподвижной системе координат a -b , то переход к новой системе координат x-y, развернутой относительно исходной на некоторый угол J (xy) (рис. 1.2 а)), осуществляется из очевидного соотношения аргументов комплексных чисел в виде
|

|
(1.1.4) |
При этом следует заметить, что на угол J (xy)
не накладывается никаких ограничений, т.е. он может иметь постоянное
значение, но может также изменяться произвольным образом. Для системы
координат вращающейся с постоянной угловой частотой w (xy) он равен – J (xy) = w (xy)t.
Преобразование координат можно записать в развернутом виде следующим образом
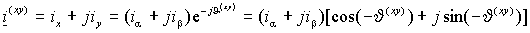 . .
Отсюда можно найти составляющие вектора ix и iy.или в матричной форме
|
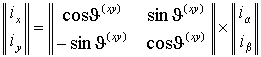 , ,
|
(1.1.5) |
а также обратное преобразование
|
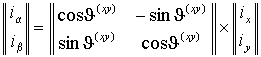 . .
|
(1.1.6) |
Преобразование
координат можно осуществить не только от неподвижной системы к
вращающейся, но и для двух систем координат, вращающихся с различными
угловыми частотами. Пусть вектор i представлен в системе координат d-q, текущий угол которой относительно неподвижных координат составляет J (dq) (рис. 1.2 б). Тогда из очевидных соотношений углов преобразование координат можно записать в виде
|
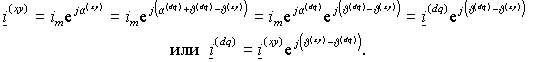
|
(1.1.7) |
Обобщенными векторами можно представить также напряжения u и потокосцепления y , при этом все свойства рассмотренного выше обобщенного вектора тока будут присущи и этим векторам.

1.2. Основные соотношения между токами и потокосцеплениями АД.
Если
пренебречь насыщением магнитопровода АД, то магнитные потоки,
сцепляющиеся с его обмотками, будут пропорциональны соответствующим МДС.
Рассмотрим основные соотношения между этими величинами. 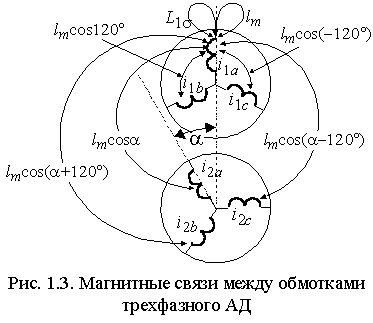
Допустим,
что статор и ротор трехфазного АД симметричны, параметры обмотки ротора
приведены к обмотке статора и рабочий зазор машины равномерный.
Схематически эти обмотки показаны на рис. 1.3.
С обмоткой фазы a
статора сцепляются магнитные потоки, создаваемые как ею самой, так и
всеми остальными обмотками. Часть магнитного потока, создаваемого самой
обмоткой сцепляется только с ее собственными витками и называется потоком рассеяния. Другая часть, помимо витков самой обмотки охватывает также витки других обмоток и называется главным или основным магнитным потоком. Индуктивность L1s , связывающая поток рассеяния обмотки с протекающим в ней током, называется индуктивностью рассеяния, а индуктивность lm, определяющая потокосцепление с основным потоком – взаимной индуктивностью или индуктивностью основного потока. Пользуясь этими величинами, можно представить потокосцепление фазы a при отсутствии токов в обмотках ротора в виде
|
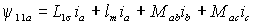 , ,
|
(1.2.1) |
где Mab и Mac – взаимные индуктивности статорных обмоток.
Если две
обмотки статора АД имеют одинаковые параметры, то магнитный поток,
создаваемый током второй обмоткой и сцепляющийся с витками первой, будет
полностью идентичен потоку, создаваемому первой обмоткой и сцепляющимся
с витками второй, при условии одинаковых токов и совпадения
расположения осей двух обмоток в пространстве. Очевидно, что при этих
условиях картина магнитного поля будет одинаковой независимо от того, по
какой из обмоток протекает ток. Следовательно, индуктивность
основного потока статорных обмоток будет равна их взаимной индуктивности
при условии совмещения геометрических осей.
Смещение осей обмоток в пространстве на угол q вызовет изменение их взаимной индуктивности, пропорциональное косинусу угла сдвига, т.е. M=M0cosq =lmcosq , где M0=lm – взаимная индуктивность обмоток при совмещении их осей. При отсутствии нулевого провода ia+ib+ic=0 Ю ib+ic=- ia и выражение (1.2.1) можно преобразовать с учетом того, что q b=120° и q c=- 120° к виду
|
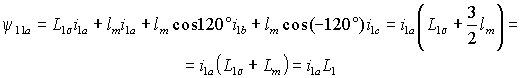 . .
|
(1.2.2) |
Индуктивность L1 соответствует полной индуктивности статорной обмотки, включающей ее индуктивность от потока рассеяния L1s , индуктивность от части основного магнитного потока, созданной самой обмоткой lm, и индуктивность от части основного потока, созданной двумя другими обмотками статора lm/2. Таким образом, полная индуктивность обмотки статора от основного магнитного потока Lm в 3/2 раза больше ее индуктивности lm, рассчитанной при отсутствии токов в других обмотках.
В силу симметрии статора, для других обмоток можно записать аналогичные выражения – 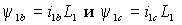 , а затем, аналогично выражению (1.1.1), объединить фазные проекции в обобщенный вектор потокосцепления статора при отсутствии токов ротора – , а затем, аналогично выражению (1.1.1), объединить фазные проекции в обобщенный вектор потокосцепления статора при отсутствии токов ротора –
|
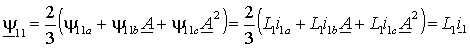 . .
|
(1.2.3) |
Следует
заметить, что при анализе индуктивностей не вводилось никаких
ограничений на пространственное распределение магнитного потока по
зазору машины, поэтому полученные выражения справедливы при любом характере распределения поля.
Наличие токов в обмотках ротора приведет к появлению дополнительных составляющих потокосцеплений обмоток статора. Если ось фазы a ротора смещена в пространстве на некоторый угол a (рис. 1.3), то взаимные индуктивности обмоток ротора и фазы a статора можно определить через соответствующие углы, образуемые их осями в виде –
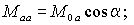
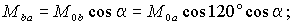
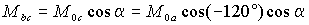
где M0a , M0b и M0c – взаимные индуктивности при a =0. Тогда полное потокосцепление обмотки фазы a статора при наличии токов ротора и с учетом того, что нулевой провод ротора отсутствует, будет
|
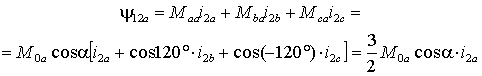
|
(1.2.4) |
Но взаимная индуктивность обмоток фазы a статора и ротора при нулевом смещении осей M0a равна lm
, т.к. параметры обмоток ротора приведены к статорным и приближенно
можно считать, что при совпадении их осей картина магнитного поля будет
такой же, как при совпадении осей статорных обмоток. Поэтому
|
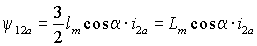
и по аналогии для двух других фаз: |
(1.2.5 а) |
|
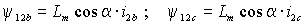
|
(1.2.5 б) |
Объединяя потокосцепления фазных обмоток в обобщенный вектор потокосцепления, получим
|
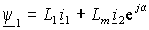 . .
|
(1.2.6) |
Аналогичное выражение, в силу симметрии связей между статором и ротором, можно записать для потокосцепления ротора –
|
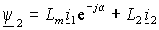 . .
|
(1.2.7) |
В
выражениях (1.2.6) и (1.2.7) векторы тока ротора и статора записаны в
различных системах координат. Так в первом выражении ток статора записан
в неподвижной системе координат a -b , связанной со статором, а ток ротора во вращающейся (смещенной на текущий угол a ) системе координат x-y, связанной с ротором, т.е. в полной записи с индексами систем координат –
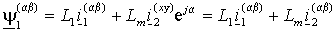
или, если обе части выражения (1.2.6) умножить на оператор поворота e- ja
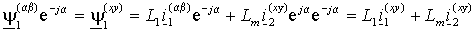 . .
Таким
образом, при записи обобщенных векторов в одинаковых системах координат
выражения для потокосцепления имеют одинаковую форму и индексы системы в
них можно опустить. Тогда
окончательно потокосцепления статора и ротора с учетом всех токов АД и
независимо от выбранной системы координат можно представить в виде
|
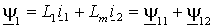 ; ;
|
(1.2.8 а) |
|
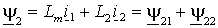 . .
|
(1.2.8 б) |
Из
выражений (1.2.8) следует, что потокосцепления статора и ротора
раскладываются на составляющие обусловленные собственным током (y 11 и y 22) и током другой части АД (y 12 и y 21).
Пользуясь тем, что сумма токов статора и ротора образует ток намагничивания АД, т.е. 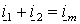 , потокоцепления статора и ротора можно также представить через основной магнитный поток , потокоцепления статора и ротора можно также представить через основной магнитный поток 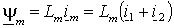 и потоки рассеяния статора и потоки рассеяния статора 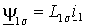 и ротора и ротора 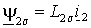 – –
|
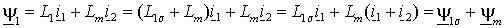 ; ;
|
(1.2.9 а) |
|
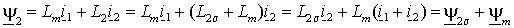 . .
|
(1.2.9 б) |

1.3. Индуктивность составляющей нулевой последовательности.
Различного
вида асимметрия параметров АД и/или источника питания вызывает при
наличии нулевого провода появления токов нулевой последовательности в
обмотках статора. Так как для нулевой составляющей справедливо ia0 = ib0 = ic0 = i0, то, подставляя эти значения в выражение (1.2.2) для потокосцепления обмотки фазы a статора, получим
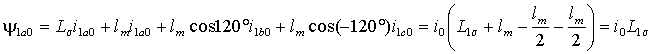 . .
Очевидно, что аналогичные выкладки для потокосцеплений обмоток фаз b и c приведут к такому же результату, т.е. y 1a0=y 1b0=y 1c0=L1s i0. Таким образом, потокосцепления составляющих нулевой последовательности для всех обмоток одинаковы и определяются индуктивностью рассеяния L1s .

1.4. Уравнения статора и ротора в векторной форме.
Уравнения Кирхгофа для фазных напряжений статора АД имею вид
|
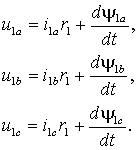
|
(1.4.1) |
При наличии нулевых составляющих к выражениям (1.4.1) следует добавить уравнение
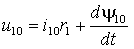 . .
Перейдем к векторной форме записи выражений (1.4.1), умножив второе уравнение на A, а третье на A2 , а затем складывая все три уравнения и умножая их правую и левую части на 2/3. В результате получим
|
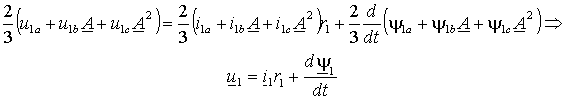
|
(1.4.2) |
Аналогичные преобразования можно выполнить с системе координат x–y и для фаз ротора, получив при этом
|
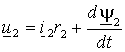 . .
|
(1.4.3) |
Уравнения (1.4.2) и (1.4.3) записаны в разных системах координат. Для перевода уравнения ротора в неподвижную систему координат a -b умножим обе его части на оператор поворота на текущий угол поворота системы координат J – ejJ и представим в производной вектор потокосцепления ротора в новой системе как 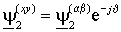 .
После преобразований, опуская индексы координатной системы, получим
уравнение ротора в векторной форме в системе координат статора .
После преобразований, опуская индексы координатной системы, получим
уравнение ротора в векторной форме в системе координат статора
|
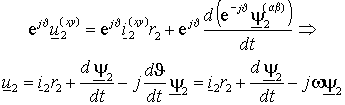 , ,
|
(1.4.4) |
где w =dJ /dt – текущая скорость вращения ротора.
Переход к
неподвижной системе координат в уравнении ротора привел к разложению
слагаемого, соответствующего ЭДС индукции, на две составляющие: первая
составляющая dy 2/dt связана с изменением потокосцепления во времени вследствие измерения во времени токов и называется ЭДС трансформации, по аналогии с процессами ее возбуждения в соответствующей электрической машине; вторая – w y 2 связана с изменением потокосцепления вследствие вращения ротора и называется ЭДС вращения.
Разложение ЭДС индукции на составляющие является математической
операцией, связанной с преобразованием системы координат при условии
инвариантности мощности и в некоторых случаях это разложение можно
истолковать, исходя из физических процессов в машине.
Уравнения (1.4.2) и (1.4.4)
записаны для неподвижной системы координат и их можно объединить в
общую систему для решения. Кроме того, оба этих уравнения можно
представить в некоторой произвольной системе координат m-n, вращающейся с произвольной угловой частотой w (mn). Для этого с ними нужно проделать преобразования аналогичные выражениям (1.4.4), в результате которых мы получим уравнения:
|
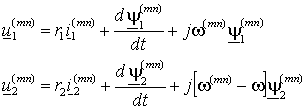 , ,
|
(1.4.5) |
из которых уравнения для любых других систем координат получаются подстановкой в (1.4.5) соответствующей частоты вращения w (mn).
Выражения (1.4.5) показывают, что выбором системы координат можно упростить задачу, исключив ЭДС вращения, но только в одном из уравнений.
В дальнейшем мы будем использовать следующие индексы систем координат:
|
a -b – |
неподвижная система координат (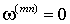 ) ориентированная по оси фазы a обмотки статора; ) ориентированная по оси фазы a обмотки статора; |
|
x-y – |
система координат, вращающаяся синхронно с ротором (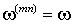 ) и ориентированная по оси фазы a его обмотки; ) и ориентированная по оси фазы a его обмотки; |
|
d-q – |
система координат, вращающаяся синхронно с потокосцеплением ротора (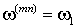 ) и ориентированная по его направлению; ) и ориентированная по его направлению; |
|
m-n – |
произвольно ориентированная система координат, вращающаяся с произвольной скоростью 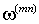 . . |
В любой электрической машине угловая частота вращения магнитного поля статора W 1 связана с угловой частотой вращения магнитного поля ротора W 2 и угловой частотой вращения ротора W следующим соотношением – 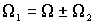 ,
где положительный знак соответствует согласному направлению вращения.
Но частоты вращения полей статора и ротора определяются частотами
соответствующих токов и числом пар полюсов обмоток zp, т.е. ,
где положительный знак соответствует согласному направлению вращения.
Но частоты вращения полей статора и ротора определяются частотами
соответствующих токов и числом пар полюсов обмоток zp, т.е. 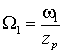 и и 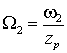 , где w 1 и w 2 – частоты токов статора и ротора. Отсюда , где w 1 и w 2 – частоты токов статора и ротора. Отсюда
|
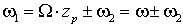
|
(1.4.6) |
где 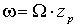 – угловая частота вращения ротора электрической машины с одной парой полюсов. – угловая частота вращения ротора электрической машины с одной парой полюсов.

1.5. Обобщенная электрическая машина.
Уравнения (1.4.3) и (1.4.4) , записанные в неподвижной системе координат a -b , можно разложить на составляющие, представив векторные величины в виде комплексных чисел
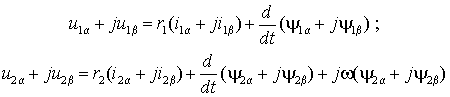
Отсюда
|
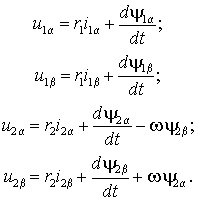
|
(1.5.1) |
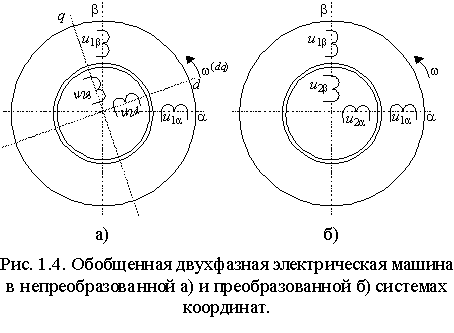
Уравнениям (1.5.1) соответствует электрическая
машина с одной парой полюсов и двумя обмотками на статоре и роторе,
расположенными на взаимно-перпендикулярных осях и неподвижными друг относительно друга (рис. 1.4). Такая электрическая машина называется обобщенной (ОЭМ).
При выводе уравнений (1.5.1) использовался ряд допущений, поэтому все они должны быть распространены и на модель обобщенной машины, т.е.:
- машина симметрична и имеет равномерный воздушный зазор;
- магнитопровод машины ненасыщен;
- МДС обмоток имеет синусоидальное распределение по рабочему зазору.
Модель
обобщенной электрической машины универсальна и при принятии
определенных условий, из нее можно получить все типы электрических машин
как частные случаи. Например, при питании обмоток статора от двух
источников переменного синусоидального тока, смещенных по фазе на 90°
, в рабочем зазоре создается круговое вращающееся магнитное поле. Если
одну из обмоток ротора подключить к источнику постоянного тока, то мы
получим модель синхронной машины. Если обе обмотки ротора замкнуть
накоротко, то образуется модель асинхронной короткозамкнутой машины.
Наконец, если одну из обмоток статора подключить к источнику постоянного
тока, а обмотки ротора подключить к двум источникам переменного синусоидального тока с частотой, равной частоте вращения ротора, и фазовым смещением в 90°
, таким образом, чтобы поле ротора вращалось в направлении
противоположном направлению вращения его вала, то мы получим модель
машины постоянного тока. В этой модели поле ротора формируется
источниками питания переменного тока с управляемой частотой, роль
которых в реальной машине играет источник постоянного тока и коллектор.
Уравнения (1.4.5) соответствуют модели обобщенной электрической машины в системе координат, вращающейся с произвольной угловой частой w (mn). Их также можно разложить на составляющие в виде
|
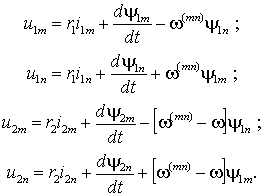
|
(1.5.2) |
Из
выражений (1.5.2) следует, что в произвольно вращающейся системе
координат ЭДС вращения существует как в статоре, так и в роторе. Наличие ЭДС вращения приводит к появлению перекрестных связей в структуре модели машины,
т.к. это слагаемое образуется проекцией потокосцепления на другую ось
координат, что существенно затрудняет построение систем управления.
Исключить ЭДС вращения можно надлежащим выбором угловой частоты вращения
системы координат, но только либо в уравнениях статора (w (mn)=0), либо в уравнениях ротора (w (mn)=w ).
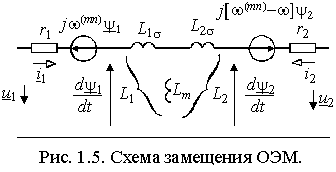
Уравнения (1.5.2) можно представить электрической схемой замещения рис. 1.5.
В короткозамкнутом АД 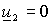 и уравнения (1.5.2) принимают вид и уравнения (1.5.2) принимают вид
|
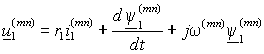 ; ;
|
(1.5.3 а) |
|
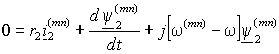 . .
|
(1.5.3 б) |
При
этом отсутствие внешнего источника электрической энергии, питающего
ротор короткозамкнутого АД, определяет следующее соотношение частот
статора и ротора в уравнениях (1.5.3) –
|
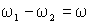 , ,
|
(1.5.4) |
1.5.1. Электромагнитный момент АД.
Основной
конечной величиной характеризующей электромеханическое преобразование
является электромагнитный момент на валу. Он образуется в результате
взаимодействия магнитного поля и тока, протекающего в обмотках статора
или ротора, и может быть представлен как векторное произведение
|
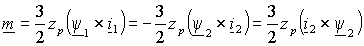 , ,
|
(1.5.5) |
где – zp число пар полюсов машины. Можно также, воспользовавшись выражениями (1.2.8), представить его в виде –
|
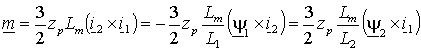 . .
|
(1.5.6) |
В
выражениях (1.5.5) и (1.5.6) физический смысл имеет только модуль
вектора электромагнитного момента и его можно определить через проекции
векторов сомножителей. Для произвольных векторов a и b модуль векторного произведения равен разности скалярных произведений проекций векторов на ортогональные оси координат, т.е. –
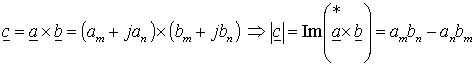
Поэтому любое из выражений (1.5.5) и (1.5.6) позволяет найти модуль электромагнитного момента |m|=m, выразив входящие в него векторы через их проекции на координатные оси m-n. Например, электромагнитный момент определяется через произведение потокосцепления ротора на ток ротора в виде
|
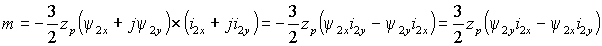 . .
|
(1.5.7) |

1.6. Модель короткозамкнутого АД при частотном управлении.
Асинхронный
привод с частотным управлением является в настоящее время наиболее
распространенным. Однако его динамика чаще всего исследуется с помощью
упрощенных моделей с отклонениями в малом. Векторная модель АД позволяет
получить точную структурную схему, которую затем можно исследовать
современными средствами компьютерного моделирования. Рассмотрим на этом
примере методику получения передаточных функций сложных объектов с
помощью векторных уравнений ОЭМ.
Пусть система
координат модели АД ориентирована по вектору напряжения статора. Тогда
ее угловая частота вращения будет определяться частотой сети 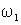 и из выражений (1.5.3) с учетом того, что и из выражений (1.5.3) с учетом того, что 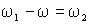 , мы получим – , мы получим –
|
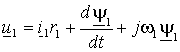 ; ;
|
(1.6.1) |
|
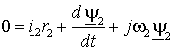 . .
|
(1.6.2) |
Для вычисления модуля электромагнитного момента АД m используем векторы потокосцепления статора 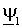 и тока ротора и тока ротора 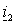 , подставляя в (1.5.6) выражение для тока статора , подставляя в (1.5.6) выражение для тока статора 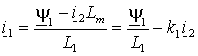 , полученное из выражения (1.2.8 а), т.е. , полученное из выражения (1.2.8 а), т.е.
|
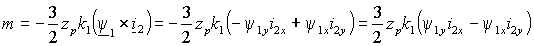 , ,
|
(1.6.3) |
где 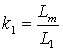 – коэффициент связи статора. – коэффициент связи статора.
При указанном выборе векторов, определяющих электромагнитный момент, нужно с помощью выражений (1.2.8) исключить в уравнениях (1.6.2) и (1.6.3) векторы 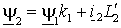 и и 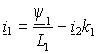 . Тогда, переходя к операторным функциям, получим . Тогда, переходя к операторным функциям, получим
|
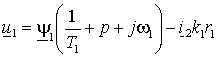 ; ;
|
(1.6.4) |
|
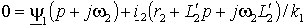
|
(1.6.5) |
где: 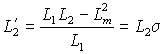 , , 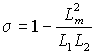 – коэффициент рассеяния, а – коэффициент рассеяния, а 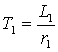 – электромагнитная постоянная времени статора. – электромагнитная постоянная времени статора.
Вычитая из уравнения (1.6.4) уравнение (1.6.5), можно понизить порядок уравнения –
|
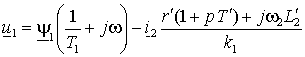
|
(1.6.6) |
где: 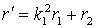 , а , а 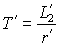 . .
Разделим векторы в выражении (1.6.6) на вещественные и мнимые составляющие и выразим проекции тока ротора
|
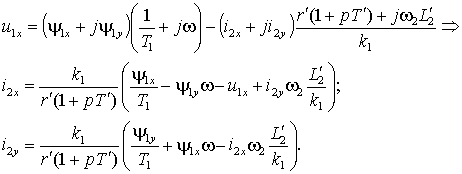
|
(1.6.7) |
Выражения (1.6.7) позволяют построить структурную схему преобразования напряжения 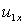 и частоты и частоты 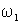 статора в фазные токи ротора статора в фазные токи ротора 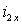 и и 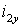 обобщенного АД при известных проекциях вектора потокосцепления статора обобщенного АД при известных проекциях вектора потокосцепления статора 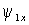 , , 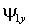 и частоты вращения ротора и частоты вращения ротора 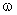 . Но потокосцепление статора можно выразить через ток ротора с помощью выражения (1.6.4) – . Но потокосцепление статора можно выразить через ток ротора с помощью выражения (1.6.4) –
|
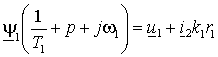 . .
|
(1.6.8) |
Разделяя вещественную и мнимую составляющие, получим
|
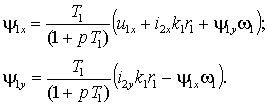
|
(1.6.9) |
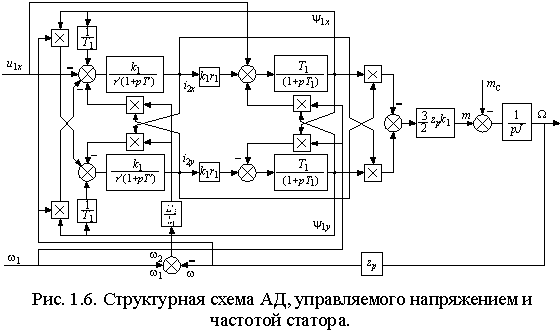
Тогда, с учетом основного уравнения привода 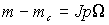 , мы получим структурную схему АД, приведенную на рис. 1.6. , мы получим структурную схему АД, приведенную на рис. 1.6.
Как
следует из рисунка, структура АД нелинейна и имеет четыре перекрестных
связи. Упростить ее для получения передаточных функций по каналам
управления напряжением и частотой крайне затруднительно, но не
представляет большого труда построить эту модель в системе MatLab/Simulink и получить требуемые характеристики привода при различных законах управления, связывающих какой-либо функцией U=F(w) входы управления частотой и напряжением статора.

2. ВЕКТОРНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМ ДВИГАТЕЛЕМ
2.1 Общий принцип векторного управления АД.
Как
известно, полная управляемость электропривода обеспечивается, если
обеспечивается управление электромагнитным моментом двигателя. В случае
АД для построения системы управления можно использовать выражения (1.5.5)–(1.5.6)
и другие производные от этих выражений. Для этого требуется независимо
управлять координатами векторов, входящих в выбранное уравнение
электромагнитного момента. Выбор уравнения для построения системы
управления играет большую роль, т.к. многие величины, в особенности у короткозамкнутых
АД, не могут быть измерены. Кроме того, этот выбор существенно влияет
на сложность передаточных функций системы, иногда в несколько раз
увеличивая порядок уравнений. Однако при любом выборе структура
выражения электромагнитного момента будет аналогичной (1.5.7) и общий принцип моделирования и построения системы управления АД заключается
в том, что для этого используется система координат, постоянно
ориентированная по направлению какого-либо вектора, определяющего
электромагнитный момент. Тогда проекция этого вектора на другую ось
координат и соответствующее ей слагаемое в выражении для
электромагнитного момента будут равны нулю, и формально оно принимает
вид, идентичный выражению для электромагнитного момента двигателя
постоянного тока, который пропорционален по величине току якоря и основному магнитному потоку.
Выбор вектора,
по направлению которого ориентируется координатная система, произволен и
определяется только простотой и возможностью реализации модели АД.
Например, в случае ориентации по потокосцеплению ротора (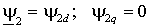 ) момент можно представить как ) момент можно представить как
|
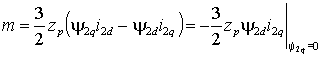 или или
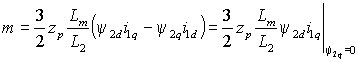 . .
|
(2.1.1) |
Очевидно,
что первое выражение для управления короткозамкнутым АД не представляет
интереса, т.к. включает практически неподдающийся измерению и
управлению ток ротора, в то время как второе, позволяет при
условии постоянства потокосцепления ротора управлять электромагнитным
моментом изменением проекции тока статора на поперечную ось i1q.
Таким
образом, для построения системы векторного управления АД нужно выбрать
вектор, относительно которого будет ориентирована система координат, и
соответствующее выражение для электромагнитного момента, а затем
определить, входящие в него величины из уравнений (1.5.3) для цепи статора и/или ротора.

2.2. Модель АД, управляемого током статора, в системе координат, ориентированной по потокосцеплению ротора.
Если
в качестве опорного вектора выбрать потокосцепление ротора и
ориентировать по нему координатную систему так, чтобы ее вещественная
ось совпадала с направлением y 2,то угловая частота вращения системы координат w (mn)= w (dq) будет равна угловой частоте питания статора w 1, т.к. векторы потокосцеплений статора и ротора вращаются с одинаковой частотой. Тогда из уравнения (1.5.3) для цепи ротора и с учетом того, что w 1- w =w 2, уравнение ротора имеет вид
|
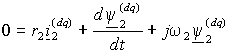 . .
|
(2.2.1) |
В это уравнение в качестве переменной входит неконтролируемый ток ротора. Поэтому из выражения (1.2.8 б) для потокосцепления y 2 найдем 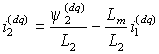 и заменим его в выражении (2.2.1). Тогда, опуская далее индексы системы координат, получим и заменим его в выражении (2.2.1). Тогда, опуская далее индексы системы координат, получим
|
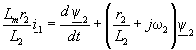 . .
|
(2.2.2) |
Преобразуем уравнение (2.2.2) по Лапласу и введем в него электромагнитную постоянную времени ротора 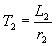 , ,
|
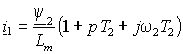 . .
|
(2.2.3) |
Отсюда найдем проекции вектора тока статора с учетом того, что y 2q=0
|
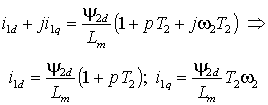
|
(2.2.4) |
а также потокосцепление и угловую частоту ротора
|
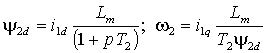
|
(2.2.5) |
Таким образом, с помощью проекции тока статора i1d можно управлять потокосцеплением ротора и передаточная функция этого канала соответствует апериодическому звену с постоянной времени равной постоянной времени ротора; а с помощью проекции i1q можно независимо и безинерционно управлять частотой ротора w 2.
Подставляя i1q в выражение (2.1.1), получим
|
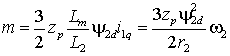 , ,
|
(2.2.6) |
т.е. частота токов ротора при заданном потокосцеплении определяет электромагнитный момент АД. 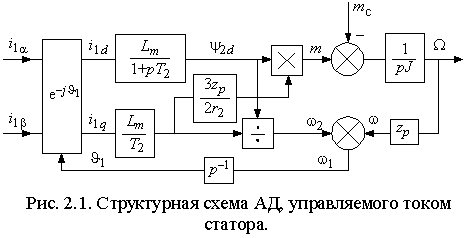
Выражения
(2.2.5) и (2.2.6) совместно с уравнением движения электропривода
позволяют построить структурную схему АД (рис. 2.1). Входными величинами
структурной схемы являются проекции вектора тока статора i1d и i1q в координатной системе ориентированной по потокосцеплению ротора, а также момент сопротивления на валу АД mc. Выходными величинами – угловая частота токов ротора w 2 и вращения вала w , а также соответствующая им частота статора w 1=w +w 2.
Из выражения (2.2.6) следует, что при постоянном потокосцеплении и частоте ротора электромагнитный момент АД также является константой и не зависит от частоты вращения, т.е. при изменении частоты вращения w в любых пределах частота статора w 1 изменяется таким образом, чтобы выполнялось условие – w 1–w =w 2=const. При этом АД обладает абсолютно мягкой механической характеристикой. 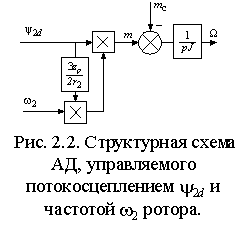
В
реальном АД ток статора формируется в неподвижной системе координат,
поэтому его модель содержит внутренний блок вращения вектора тока или ротатор (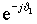 рис. 2.1), с помощью которого осуществляется переход от неподвижной системы координат a -b к системе d-q, ориентированной по потокосцеплению. Текущий угол поворота вектора тока определяется частотой статора рис. 2.1), с помощью которого осуществляется переход от неподвижной системы координат a -b к системе d-q, ориентированной по потокосцеплению. Текущий угол поворота вектора тока определяется частотой статора 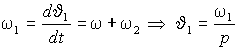 . .
Выражения (2.2.4)–(2.2.6)
определяют связь между проекциями тока статора на оси координат,
потокосцеплением, частотой ротора и электромагнитным моментом АД. Из
выражения (2.2.6) и уравнения движения следует, что управление моментом может осуществляться безинерционно
двумя входными сигналами: потокосцеплением и частотой ротора в
соответствии со структурной схемой рис. 2.2. Но эти сигналы связаны с
проекциями вектора тока статора выражениями (2.2.5). Поэтому, если построить блок управления, реализующий передаточные функции в соответствии с выражениями (2.2.4),
и называемый блоком развязки координат (РК), а также ротатор, вращающий
вектор тока статора в направлении противоположном действию внутреннего
ротатора АД (рис. 2.3), то входными сигналами для этого устройства
управления будут потокосцепление и частота ротора. Название блока
развязки координат происходит от выполняемой им функции формирования
сигналов, соответствующих независимым (развязанным, разделённым) проекциям вектора тока статора. 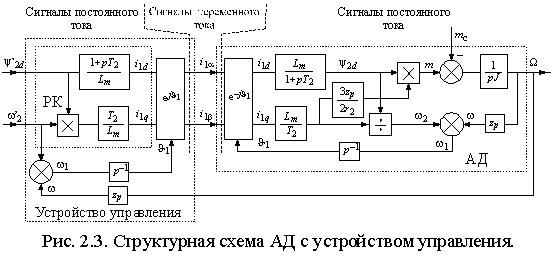
По
структурной схеме нетрудно проследить, что передаточная функция блоков,
включенных между точками схемы соответствующими сигналам поотоксцепления
и частоты ротора равна единице (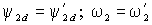 ), т.е. устройство управления по существу является частью модели АД с обратными передаточными функциями. Поэтому формально структура рис. 2.3 полностью идентична структуре рис. 2.2,
однако с помощью моделирования легко убедиться, что переходные процессы
в этих структурах существенно различаются. Это связано с тем, что в
структуре рис. 2.2 исключены инерционные звенья, присутствующие в
реальной машине и в устройстве управления, которые реализуют операции
интегрирования и дифференцирования за конечный промежуток времени. ), т.е. устройство управления по существу является частью модели АД с обратными передаточными функциями. Поэтому формально структура рис. 2.3 полностью идентична структуре рис. 2.2,
однако с помощью моделирования легко убедиться, что переходные процессы
в этих структурах существенно различаются. Это связано с тем, что в
структуре рис. 2.2 исключены инерционные звенья, присутствующие в
реальной машине и в устройстве управления, которые реализуют операции
интегрирования и дифференцирования за конечный промежуток времени.
Из выражения для электромагнитного момента (2.2.6) и общего уравнения движения можно получить передаточную функцию АД по каналу управления частотой ротора
|
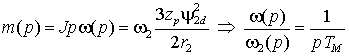 , ,
|
(2.2.7) |
где 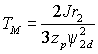 – механическая постоянная времени. Эта передаточная
функция полностью соответствует двигателю постоянного тока, поэтому
построение систем электропривода с векторным управлением АД ничем не
отличается от приводов постоянного тока. – механическая постоянная времени. Эта передаточная
функция полностью соответствует двигателю постоянного тока, поэтому
построение систем электропривода с векторным управлением АД ничем не
отличается от приводов постоянного тока.
Следует отметить, что устройство управления рис. 2.3
может выполнять свои функции только при условии, что параметры АД,
входящие в передаточные функции его звеньев соответствуют истинным
значениям, в противном случае потокосцепление и частота ротора в АД и в
устройстве управления будут отличаться друг от друга. Это обстоятельство
создает значительные трудности при реализации систем векторного
управления на практике, т.к. параметры АД изменяются в процессе работы. В
особенности это относится к значениям активных сопротивлений.

2.3. Модель АД, управляемого напряжением статора, в системе координат, ориентированной по потокосцеплению ротора.
Управление АД можно осуществлять также с помощью проекций вектора напряжения статора на оси d-q. Для этого нужно получить модель АД, в которой входными величинами являются u1d и u1q.
Если координатная система вращается вместе с потокосцеплением ротора, то ее угловая частота равна w 1, поэтому, полагая в (1.5.3 а) w (xy) =w 1, получим уравнение статора в системе координат d-q:
|
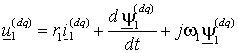 , ,
|
(2.3.1) |
а затем, выразив ток ротора 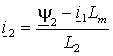 из (1.2.8б) и подставив его в (1.2.8 а), мы получим выражение для потокосцепления статора в виде: из (1.2.8б) и подставив его в (1.2.8 а), мы получим выражение для потокосцепления статора в виде:
|
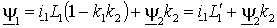 , ,
|
(2.3.2) |
где: 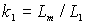 и и 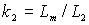 – коэффициенты связи статора и ротора; – коэффициенты связи статора и ротора; 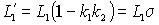 – общая индуктивность рассеяния со стороны статора. – общая индуктивность рассеяния со стороны статора.
Подставляя (2.3.2) в (2.3.1) и преобразуя это уравнение по Лапласу, получим
|
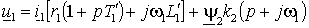 , где: , где: 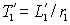 . .
|
(2.3.3) |
Разделив проекции векторов на оси d и q в уравнении (2.3.3), мы получим с учетом того, что y 2q=0, выражения для проекций напряжений статора, представленные через проекции токов статора –
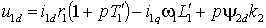 ; ;
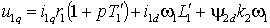 . .
Отсюда найдем выражения для проекций тока статора i1d и i1q
|
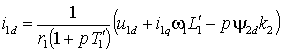 ; ;
|
(2.3.4а) |
|
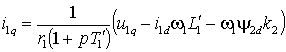 . .
|
(2.3.4б) |
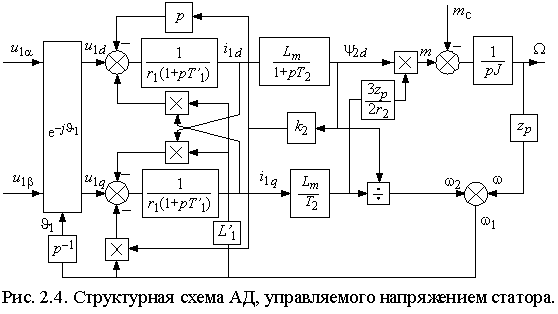
и,
используя структуру АД, управляемого током статора, построим
структурную схему АД, управляемого напряжением (рис. 2.4). Она нелинейна
и содержим перекрестные связи. Входными величинами являются проекции
напряжений статора на оси d и q – u1d и u1q.
Для приведения ее структуры к структуре рис. 2.2
нужно построить устройство управления с функциями аналогичными
устройству управления привода с заданием тока статора. С этой целью
можно использовать выражения (2.2.4), подставляя, которые в (2.3.4) получим передаточные функции блока развязки координат в виде:
|
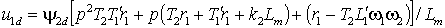 ; ;
|
(2.3.5а) |
|
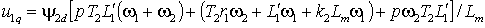
|
(2.3.5б) |
Очевидно, что
реализация этих функций затруднительна и на практике ошибки выполнения
математических операций и отклонения параметров АД от значений
включенных в передаточные функции звеньев приведут к полной
неработоспособности устройства. Облегчить задачу можно, если учесть, что
ротор АД обладает очень большой электромагнитной постоянной времени и
его потокосцепление может изменяться только относительно медленно, т.е.
|
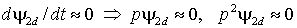 . .
|
(2.3.6) |
Тогда выражения (2.3.5) преобразуются к виду:
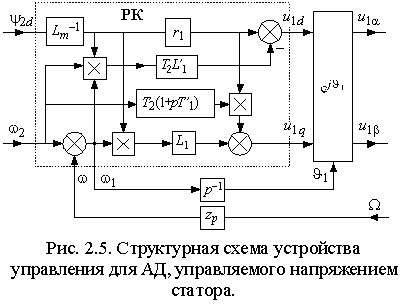
Структурная
схема устройства управления, в котором реализованы эти функции
приведена на рис. 2.5. Оно существенно сложнее, чем устройство
управления для системы c формированием тока статора АД (см. рис. 2.3).
Кроме того, в нем использованы приближенные выражения (2.3.7), вносящие
ошибку в динамических режимах, если не выполняются условия (2.3.6).

2.4. Основные элементы систем векторного управления АД.
2.4.1. Усилитель мощности релейного типа. 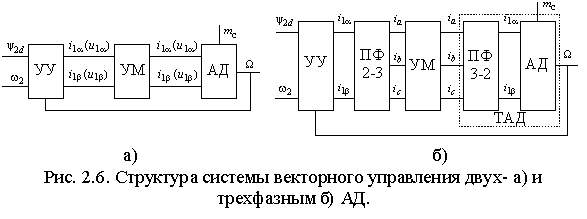
Независимо
от того, какой вектор используется для управления АД (тока или
напряжения), на выходе устройства управления формируются синусоидальные
сигналы с переменой амплитудой, частотой и фазой, соответствующие
мгновенным значениям проекций вектора тока или напряжения статора на
неподвижные оси координат. Эти сигналы должны быть усилены по мощности с
минимальными искажениями. Поэтому между выходом устройства управления
(УУ) и статором АД необходимо включить усилитель мощности (УМ) (рис.
2.6). В качестве УМ могут использоваться устройства непрерывного и
дискретного типов. Очевидно, что при мощностях выше нескольких сотен
Ватт аналоговые усилители мощности не могут применяться, поэтому в
приводе с векторным управлением в основном используются транзисторные и
тиристорные инверторы с различными законами управления и
непосредственные преобразователи частоты.
Для правильной
работы системы векторного управления УМ должны обладать единичной
передаточной функцией, т.к. ошибка формирования тока или напряжения
вызывает нарушение ориентации соответствующего вектора. На практике
достаточно, чтобы частота коммутации УМ при всех режимах работы системы
приблизительно на порядок превосходила частоту основной гармоники. 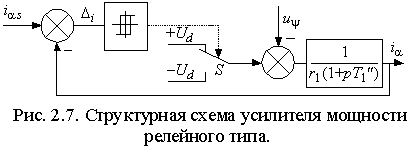
При
рассмотрении структурных схем векторного управления было отмечено, что
системы с формированием тока статора существенно проще в реализации. В
свою очередь, в дискретном УМ формирование тока
статора проще всего выполнить с помощью релейной системы управления,
показанной на рис. 2.7. В ней управление силовым ключом S
осуществляется двухпозиционным релейным элементом с гистерезисом таким
образом, что на статорную обмотку подается положительное или
отрицательное постоянное напряжение 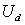 в соответствии с условиями: в соответствии с условиями:
|
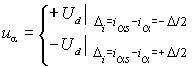 , ,
|
(2.4.1) |
где 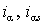 – соответственно реальный и заданный ток обмотки; D – ширина петли гистерезиса релейного элемента. – соответственно реальный и заданный ток обмотки; D – ширина петли гистерезиса релейного элемента.
В интервалах между коммутациями S
УМ представляет собой линейную систему, передаточную функцию которой
можно получить из уравнения статора в неподвижной системе координат (1.4.2) 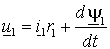 , если в нем исключить потокосцепление статора, пользуясь выражениями (1.2.9)– , если в нем исключить потокосцепление статора, пользуясь выражениями (1.2.9)–
|
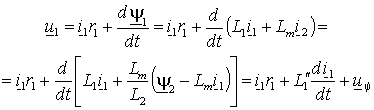 , ,
|
(2.4.2) |
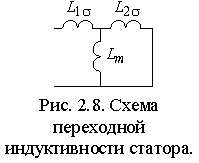
где: 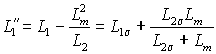 – переходная индуктивность статора; – переходная индуктивность статора; 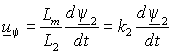 – падение напряжения создаваемое в обмотках статора магнитным потоком ротора. – падение напряжения создаваемое в обмотках статора магнитным потоком ротора.
Из выражения для переходной индуктивности статора 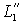 следует, что она соответствует электрической цепи рис. 2.8. Так как взаимная индуктивность Lm существенно больше индуктивности рассеяния ротора ( следует, что она соответствует электрической цепи рис. 2.8. Так как взаимная индуктивность Lm существенно больше индуктивности рассеяния ротора (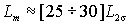 ), то с погрешность не более 2% можно считать, что ), то с погрешность не более 2% можно считать, что 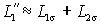 . .
Перейдем в векторном уравнении (2.4.2) к проекциям на оси координат a - b , совместив вектор напряжения статора с осью a , тогда:
|
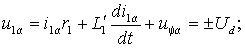
|
(2.4.3 а) |
|
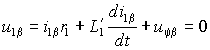
|
(2.4.3 б) |
Проекции векторов на ось a , совмещенную с осью фазной обмотки a статора, являются реальными величинами. При достаточно малом значении гистерезиса реле (D)
коммутация ключей будет происходить с высокой частотой, поэтому можно
считать, что в интервале между коммутациями напряжение, создаваемое
потоком ротора остается неизменным, т.е. 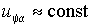 . Тогда, преобразуя выражение (2.4.3 а) по Лапласу, получим для (k+1)-го интервала между коммутациями . Тогда, преобразуя выражение (2.4.3 а) по Лапласу, получим для (k+1)-го интервала между коммутациями
|
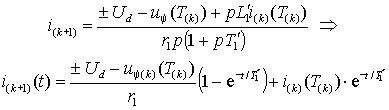 , ,
|
(2.4.4) |
где 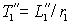 – постоянная времени переходного процесса; – постоянная времени переходного процесса; 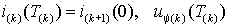 – ток статора и напряжение – ток статора и напряжение 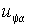 в конце k-го межкоммутационного интервала длительностью в конце k-го межкоммутационного интервала длительностью 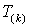 . .
Выражение
(2.4.4) можно упростить с учетом того, что длительности
межкоммутационных интервалов существенно меньше постоянной времени.
Поэтому экспоненту в первом слагаемом можно заменить касательной к ней в
начальной точке, а второе слагаемое считать константой, пренебрегая его
изменением за время 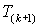 . Тогда – . Тогда –
|
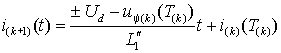 . .
|
(2.4.5) |
Знаки перед 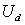 в выражениях (2.4.3ё 2.4.5) следует выбирать в соответствии с условиями (2.4.1). Для обеспечения возрастания тока необходимо выбрать значение напряжения питания в выражениях (2.4.3ё 2.4.5) следует выбирать в соответствии с условиями (2.4.1). Для обеспечения возрастания тока необходимо выбрать значение напряжения питания 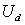 таким образом, чтобы во всех интервалах с положительными значениями таким образом, чтобы во всех интервалах с положительными значениями 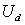 соблюдалось условие соблюдалось условие 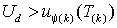 . На практике это значение выбирают из соотношения . На практике это значение выбирают из соотношения 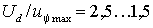 . .
Временные диаграммы работы УМ в соответствии с (2.4.5) приведены на рис. 2.9. 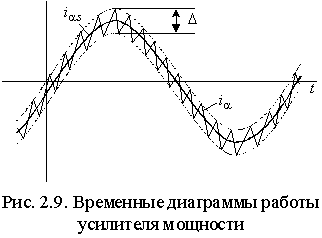
Изменение напряжения 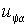 приводит к тому, что коммутация ключа S (рис. 2.7) происходит с переменной частотой. Длительность межкоммутационного интервала можно определить из выражения (2.4.5) с учетом того, что разность значений тока в начале и конце интервала равна гистерезису релейного элемента приводит к тому, что коммутация ключа S (рис. 2.7) происходит с переменной частотой. Длительность межкоммутационного интервала можно определить из выражения (2.4.5) с учетом того, что разность значений тока в начале и конце интервала равна гистерезису релейного элемента 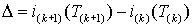 – –
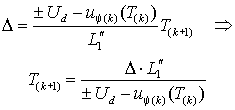
Усилитель
мощности с релейным элементом можно считать безинерционным звеном с
единичной передаточной функцией, если число коммутаций за период
формируемого тока не менее 20ё 30, а гистерезис релейного элемента не более 5ё 7% максимального значения тока.
2.4.2. Преобразователи числа фаз. 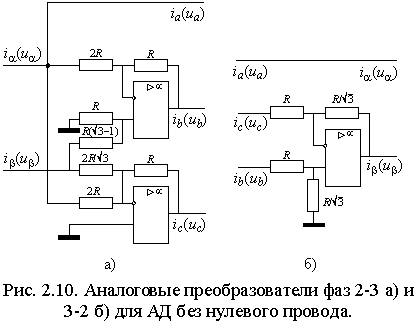
Если
АД имеет трехфазную обмотку статора, то его структурная схема содержит
внутренний преобразователь числа фаз (ПФ 3-2 на рис. 2.6), реализующий
преобразование в соответствии с выражениями (1.1.3) для токов или напряжений статора. В этом случае УМ также должен быть трехфазным, а его вход должен подключаться к выходу УУ через преобразователь (ПФ 2-3 на рис. 2.6) с обратной передаточной функцией, т.е. соответствующей выражениям (1.1.2). Пример реализации такого преобразователя на основе операционных усилителей показан на рис. 2.10 а).
В цифровых системах управления преобразование числа фаз осуществляется реализацией функций (1.1.2) и (1.1.3) .
2.4.3. Вектор-анализаторы и ротатор.
Для
ориентации системы координат векторной системы управления необходимо
определить текущее положение опорного вектора. Устройства реализующие
эти функции обычно называются вектор-анализаторами.
Если в системе
векторного управления требуется стабилизация потокосцепления, то его
текущее значение нужно либо измерить, либо вычислить по другим
величинам. Измерение потокосцепления не всегда возможно или желательно,
т.к. требует установки в АД соответствующих датчиков и, кроме того, при
снижении частоты вращения отношение полезного сигнала к шуму на выходе
датчиков снижается настолько, что их использование становится
невозможным.
В случае
потокосцепления ротора его измерение практически невозможно и обычно
производится вычисление. Проще всего оно осуществляется, если исходными
величинами являются основное потокосцепление и ток статора. Из выражений
(1.2.8 б) и (1.2.9) потокосцепление и ток ротора равны
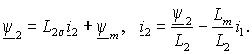
Отсюда
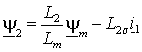
или после разложения на составляющие в неподвижной системе координат, связанной со статором
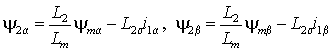 . .
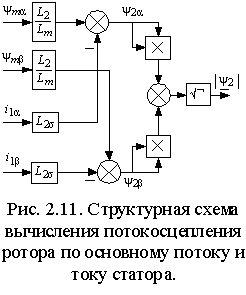
Искомый модуль вектора потокосцепления ротора затем находится по теореме Пифагора 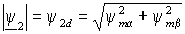 . Структурная схема соответствующего блока вычисления приведена на рис. 2.11. . Структурная схема соответствующего блока вычисления приведена на рис. 2.11.
Основное потокосцепление y 0 можно измерить, установив два датчика Холла так, чтобы один находился на оси обмотки фазы a, а другой на перпендикулярной оси. Тогда выходные сигналы датчиков будут пропорциональны y ma и y mb . Составляющие тока статора i1a и i1b получаются из фазных токов преобразованием 3-2 в соответствии с выражениями (1.1.2). 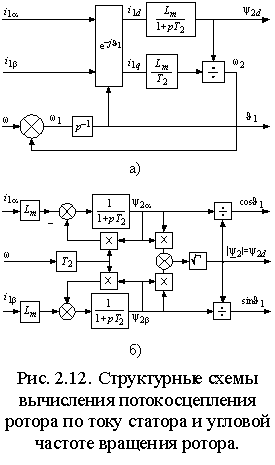
Потокосцепление
можно определить и не прибегая к измерению магнитного потока.
Достаточно измерить токи статора и угловую частоту вращения ротора. При
этом вычисление можно производить во вращающейся или в неподвижной
системе координат. Входными величинами в обоих случаях являются токи
статора в неподвижной системе координат i1a и i1b и угловая частота вращения ротора w . Выходными – модуль вектора потокосцепления ротора |y 2|=y 2d и, если требуется, текущее значение его аргумента J 1. Для вращающейся системы их связь с потокосцеплением ротора определяется выражением (2.2.5), а соответствующая ей структурная схема приведена на рис. 2.12 а).
Векторное уравнение ротора в неподвижной системе координат можно получить из выражения (1.4.5), положив w (mn) =0. Тогда
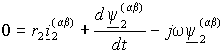 . .
Отсюда, подставив 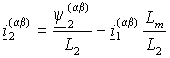 , перейдя к изображениям и опуская индексы системы координат, получим , перейдя к изображениям и опуская индексы системы координат, получим
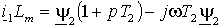 . .
Раскладывая
векторы тока статора и потокосцепления ротора на вещественную и мнимую
составляющие, получим выражения для проекций потокосцепления в
неподвижной системе координат
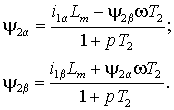
Этим выражениям соответствует структурная схема рис. 2.12 б), в которой затем по проекциям определяются модуль вектора, а также косинус и синус его аргумента –
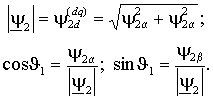
Очевидно,
что вычисление потокосцепления без использования датчиков магнитного
потока требует построения значительно более сложных устройств, однако в
некоторых случаях такое решение оправдано, т.к. установка датчиков и
формирование в них выходного сигнала также является достаточно сложной
задачей. Кроме того, устройства подобные изображенным на рис. 2.12
могут использоваться в системах асинхронного привода для создания
контуров стабилизации магнитного потока ротора, т.е. стабилизации его
модуля, что позволяет получить при частотном управлении механические
характеристики с одинаковой жесткостью рабочих участков при всех
частотах питания, что существенно расширяет диапазон регулирования АД. 
Необходимым
элементом системы векторного управления АД является ротатор,
осуществляющий преобразование координат векторов в соответствии с
выражениями (1.1.5) и (1.1.6). Если сигналы синуса и косинуса угла поворота J 1
формируются другим блоком, то ротатор легко реализуется по схеме рис.
2.13. Для вращения в положительном направлении, т.е. для реализации
функции 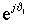 , на синусный вход ротатора подается сигнал , на синусный вход ротатора подается сигнал 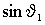 . Изменение направления вращения осуществляется либо инвертированием сигнала . Изменение направления вращения осуществляется либо инвертированием сигнала 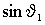 , либо инвертированием сигнала J 1. , либо инвертированием сигнала J 1.
В случае, если входным сигналом ротатора является угол J 1,
то схема рис. 2.13 должна быть дополнена блоками вычисления функций
синуса и косинуса, что очень сложно реализовать практически в аналоговой
форме, но легко выполнить в цифровой с помощью соответствующей
программы процессора или аппаратно с помощью тригонометрической таблицы,
хранящейся в ПЗУ.

2.5. Замкнутые системы векторного управления АД. 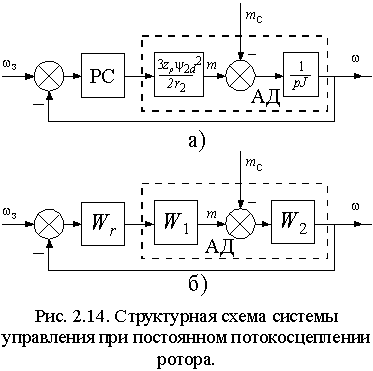
Рассмотренная
выше модель АД с векторным управлением, в которой входными сигналами
являются потокосцепление и частота ротора, является наиболее простой и
распространенной на практике. Она позволяет создавать высокоэффективные
системы управляемого асинхронного электропривода аналогичные системам
привода постоянного тока. Рассмотрим вопросы построения векторной
системы управления скоростью вращения АД.
В соответствии с выражением (2.2.7)
передаточная функция канала управления частотой ротора или, что тоже
самое, электромагнитным моментом при условии стабилизации
потокосцепления ротора соответствует интегрирующему
звену, что позволяет представить его структурную схему в замкнутой
системе управления скоростью вращения с виде рис. 2.14 а) или в общем
виде, как показано на рис. 2.14 б), где wз– заданная угловая частота вращения ротора, а Wr – передаточная функция регулятора скорости.
Передаточные функции по управлению и по возмущению можно представить в общем виде как
|
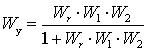 , ,
|
(2.5.1) |
|
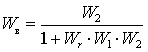 . .
|
(2.5.2) |
Для получения статической системы используют пропорциональный (П) регулятор с передаточной функций
|
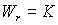 . .
|
(2.5.3) |
Если
требуется получить астатическую систему, используют
пропорционально-интегральный (ПИ) регулятор скорости с передаточной
функцией
|
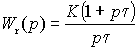 . .
|
(2.5.4) |

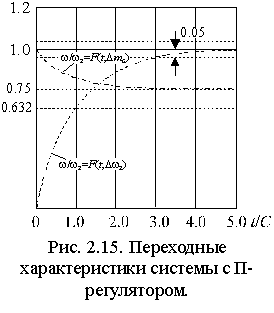
2.5.1. Характеристики системы с П-регулятором скорости.
 В случае П-регулятора передаточные функции по управлению и возмущению приобретают вид В случае П-регулятора передаточные функции по управлению и возмущению приобретают вид
|
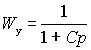 ; ;
|
(2.5.5) |
|
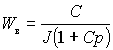 , ,
|
(2.5.6) |
где 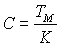 ; ; 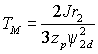 . .
Переходные характеристики привода соответствуют экспоненте с постоянной времени C, значение которой обратно пропорционально коэффициенту усиления регулятора K (рис. 2.15). Длительность переходного процесса равна 3Ч C.
Общая передаточная функция системы с П-регулятором имеет вид
|
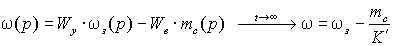
|
(2.5.7) |
и переходит в уравнение регулировочной и механической характеристик при  , где , где 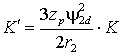 . . 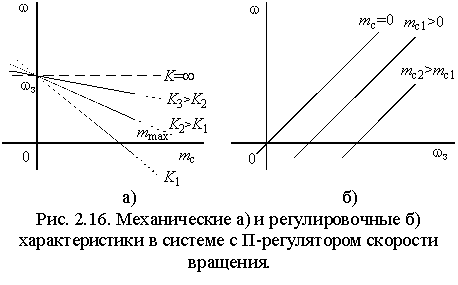
Таким
образом, статические характеристики системы векторного управления АД
имеют вид, соответствующий характеристикам двигателя постоянного тока
(ДПТ) с якорным управлением (рис. 2.16). Их жесткость пропорциональна коэффициенту усиления регулятора K, а статическая ошибка привода – обратно пропорциональна значению этого коэффициента.
Формально
характеристики могут продолжаться в любую сторону до бесконечности, но,
также как в ДПТ, ток машины должен быть ограничен значениями допустимыми
по условиям ее эксплуатации, а также по условиям эксплуатации питающего
преобразователя. В системе управления ДПТ ток якоря легко ограничить
введением после регулятора скорости звена с насыщением. В системе с
векторным управлением АД ток статора содержит две составляющие –
продольную и поперечную (i1d и i1q),
воздействующие соответственно на потокосцепление и электромагнитный
момент. Поэтому ограничение управляющих токов на входе усилителя
мощности системы недопустимо, т.к. может вызвать уменьшение
потокосцепления, и ограничение тока статора можно осуществлять только за
счет его поперечной составляющей.
Расчет максимально возможного электромагнитного момента можно произвести исходя из заданного значения потокосцепления ротора 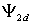 и максимально допустимого амплитудного значения тока статора и максимально допустимого амплитудного значения тока статора 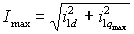 , где , где 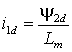 . Отсюда – . Отсюда – 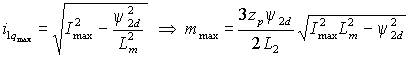 . Для сохранения покосцепления звено с насыщением, рассчитанным на значение . Для сохранения покосцепления звено с насыщением, рассчитанным на значение 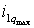 нужно вводить в канал поперечной составляющей тока системы управления (рис. 2.3). нужно вводить в канал поперечной составляющей тока системы управления (рис. 2.3).
В режиме ограничения тока АД с векторным управлением имеет абсолютно мягкую механическую характеристику.
2.5.2. Характеристики системы с ПИ-регулятором скорости.
Как следует из рисунка 2.14, передаточная характеристика W1
является константой и стандартная настройка ПИ-регулятора невозможна.
Попытаемся произвести настройку, исходя из общих принципов коррекции
характеристик системы.
После подстановки в выражение (2.5.2) передаточной функции регулятора (2.5.4) мы получим передаточную функцию системы по управлению и соответствующую частотную характеристику –
|
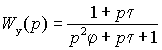 , ,
|
(2.5.8) |
|
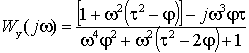 , ,
|
(2.5.9) |
где 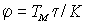 . .
Для
приближения значения модуля частотной характеристики к единице в
возможно более широком диапазоне частот исключим в знаменателе
составляющую 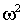 , т.е. выберем значения коэффициента , т.е. выберем значения коэффициента 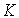 и постоянной времени и постоянной времени 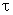 регулятора скорости так, чтобы выполнялось условие регулятора скорости так, чтобы выполнялось условие
|
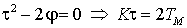 . .
|
(2.5.10) |
Тогда выражения (2.5.8) и (2.5.9) примут вид
|
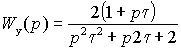 , ,
|
(2.5.11) |
|
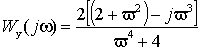 , ,
|
(2.5.12) |
где 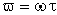 – приведенная угловая частота. – приведенная угловая частота.
С учетом соотношений (2.5.10) можно представить передаточную функцию системы по возмущению в виде
|
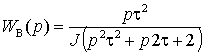 . .
|
(2.5.13) |
Выражения (2.5.11) и (2.5.13) имеют одинаковые характеристические уравнения, корни которых
|
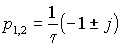 , ,
|
(2.5.14) |
соответствуют
асимптотически устойчивой системе с колебательным переходным процессом с
относительным затуханием и частотой равными друг другу. Причем, т.к.
может 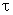 изменяться от 0 до µ , то корневые годографы системы всегда лежат в левой полуплоскости. изменяться от 0 до µ , то корневые годографы системы всегда лежат в левой полуплоскости. 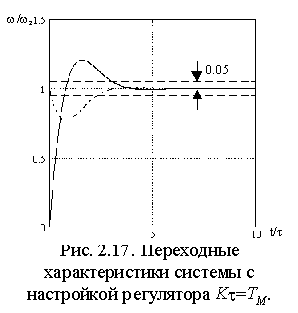
Реакция системы на скачки управляющего 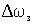 и возмущающего и возмущающего 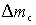 воздействий может быть получена из выражений (2.5.11) и (2.5.13) как воздействий может быть получена из выражений (2.5.11) и (2.5.13) как
|
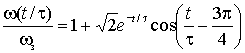
|
(2.5.15) |
|
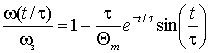 , ,
|
(2.5.16) |
где 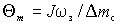 . В этих выражениях время приведено к постоянной времени регулятора скорости . В этих выражениях время приведено к постоянной времени регулятора скорости 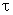 . В результате временные параметры переходных функций получаются независимыми от параметров АД (рис. 2.17). . В результате временные параметры переходных функций получаются независимыми от параметров АД (рис. 2.17).
Следует заметить, что система не накладывает каких-либо ограничений на значение 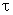 , т.к. условие настройки всегда можно выполнить соответствующим выбором , т.к. условие настройки всегда можно выполнить соответствующим выбором 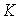 . Поэтому масштаб времени переходных функций, а, следовательно, и длительность переходного процесса может выбираться произвольно. . Поэтому масштаб времени переходных функций, а, следовательно, и длительность переходного процесса может выбираться произвольно.
Анализ выражений (2.5.15) и (2.5.16) показывает:
- перерегулирование при скачке управляющего воздействия не зависит от параметров АД
и выбора постоянной времени регулятора 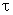 и всегда составляет 20,8%; и всегда составляет 20,8%;
- максимальное отклонение скорости вращения при скачке момента нагрузки зависит от параметров АД и нагрузки, а также от выбора
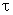 так, что с изменением так, что с изменением 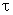 пропорционально изменяется масштаб обеих осей переходной функции пропорционально изменяется масштаб обеих осей переходной функции ;
- максимальные отклонения скорости вращения при скачках управления и момента наступают соответственно при
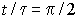 и и 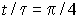 ;
- переходный процесс заканчивается после первого экстремума и составляет для скачка управления 3,07
t .
Таким
образом, предлагаемая настройка ПИ регулятора обладает универсальными
параметрами переходного процесса и позволяет получить хорошее качество
системы в тех случаях, когда невозможно осуществить стандартную
настройку.
Пользуясь выражениями (2.5.11) и (2.5.13), можно получить общую передаточную характеристику системы и соответствующие статические характеристики в виде –
|
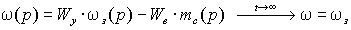 . .
|
(2.5.17) |
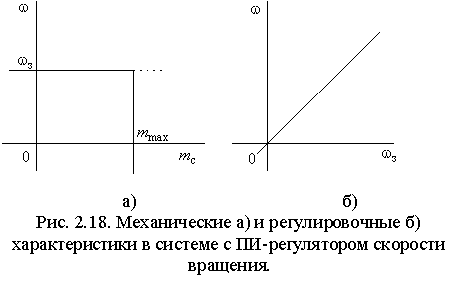
Как
и следовало ожидать, полученная система обладает астатизмом первого
порядка и абсолютно жесткой механической характеристикой в пределах
линейной зоны ограничителя тока (рис. 2.18).
Вопросы
ограничения тока, рассмотренные для системы с П-регулятором скорости, и
связанного с этим ограничения момента в полной мере относятся и к систем
с ПИ-регулятором.

Список литературы.
- Ковач К.П., Рац И. Переходные процессы в машинах переменного тока.–М.-Л.: Госэнергоиздат, 1963.–744 с.
- Казовский Е.Я. Переходные процессы в электрических машинах переменного тока.–Л.: Изд. Академии наук СССР, 1962.–624 с.
- Постников
И.М. Обобщенная теория и переходные процессы электрических машин.
Учебник для вузов, изд. 2-е.–М.: "Высш. школа", 1975.–319 с.
- Копылов И.П. Математическое моделирование электрических машин: Учеб. для вузов, 2-е изд.–М.: Высш. шк., 1994.–318 с.
- Асинхронные электроприводы с векторным управлением/ В.В. Рудаков, И.М. Столяров, В.А. Дартау.–Л.: Энергоатомиздат, 1987.–136 с.
- Системы
подчиненного регулирования электроприводов переменного тока с
вентильными преобразователями/ О.В. Слежановский, Л.Х. Дацковский, И.С.
Кузнецов и др.–М.: Энергоатомиздат, 1983.–256с.
- Schцnfeld R. Digitale Regelung elektrischer Antriebe.–Berlin: Verl. Technik, 1987.–210 S.
Использован материал: http://ets.ifmo.ru/usolzev/posobie1/vect_upr.htm
| 
