назад | ОГЛАВЛЕНИЕ | вперед
3.1. Линейные преобразования обобщенной машины
Произведём
линейные преобразования уравнений обобщённой электрической машины для
устранения зависимости индуктивностей и взаимных индуктивностей обмоток
двигателя от угла поворота ротора, возможности оперировать не синусоидально
изменяющимися переменными, а их амплитудами. При этом осуществляется замена
действительных переменных новыми переменными при условии сохранения
адекватности математического описания исследуемой машины. Этим условием
является требование инвариантности мощности при преобразовании уравнений.
Рассмотрим
преобразования, которые позволяют перейти от действительных переменных,
определяемых системой координат, жёстко связанных со статором
(α, β) и
ротором (d, q), к
расчётным переменным, соответствующим системе координат u, v, вращающихся в пространстве с произвольной скоростью ωk .
В общем виде каждую реальную переменную – напряжение, ток,
потокосцепление изобразим в виде вектора 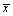 , направление которого жёстко связано с соответствующей
данной обмотке системой координат, а модуль вектора изменяется в соответствии с
изменениями изображаемой переменной. , направление которого жёстко связано с соответствующей
данной обмотке системой координат, а модуль вектора изменяется в соответствии с
изменениями изображаемой переменной.
Графические
построения, соответствующие статору и ротору изобразим отдельно, причём 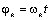 (рис. 3.3). (рис. 3.3).
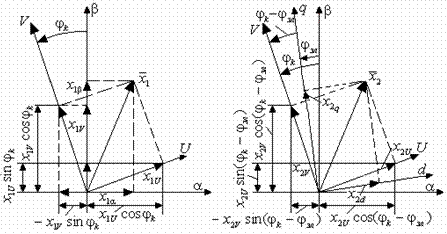
а) б)
Рис.
3.3. К преобразованию переменных статорной обмотки в системах координат (  ) и (u, v) (a) и роторной обмотки в
системах координат (d, q) и (u, v) (б). ) и (u, v) (a) и роторной обмотки в
системах координат (d, q) и (u, v) (б).
Составляющие вектора 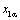 определены как
проекции векторов определены как
проекции векторов 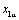 и и 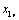 на ось α, составляющие вектора на ось α, составляющие вектора
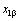 определены как проекции векторов определены как проекции векторов 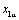 и и 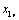 на ось β; составляющие вектора на ось β; составляющие вектора 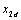 - как проекции векторов - как проекции векторов 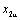 и и 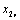 на ось d, составляющие вектора на ось d, составляющие вектора 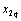 - как проекции векторов - как проекции векторов 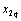 и и 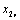 на ось q. на ось q.
Просуммировав
проекции по осям, получим формулы обратного преобразования координат обобщённой
машины, т.е. формулы перехода от расчётных к реальным
переменным:
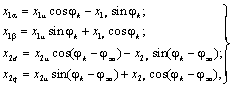 (3.2) (3.2)
где
α, β - оси, жёстко
связанные со статором;
d, q - оси, жёстко
связанные с ротором;
u, v – произвольная система ортогональных координат, вращающихся
относительно статора со скоростью ωk, а φэл=pnφ;
φk=ωkt,
где
φэл и φ – соответственно электрический и геометрический углы
поворота ротора относительно статора; pn
– число пар полюсов.
Аналогично выводятся формулы прямого преобразования:
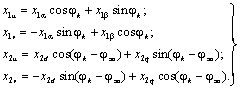 (3.3) (3.3)
Подставив
(3.2) в первые два уравнения (3.1), получим:
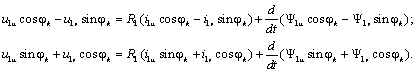
Умножив первое уравнение на cosφ k , а второе на sinφ k ,
сложив их, и учитывая, что
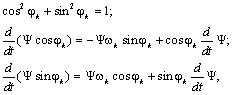
получим:
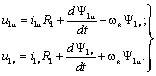 (3.4) (3.4)
В результате таких же преобразований для роторных цепей обобщенной
машины получим:
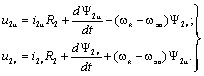 (3.5) (3.5)
где
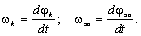
Уравнение
электромагнитного момента для неявнополюсной машины выводится аналогично изложенному выше:
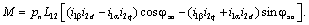 (3.6) (3.6)
Воспользовавшись формулами обратного
преобразования, получим:
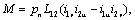
где
L12 –
взаимная индуктивность между обмотками статора и ротора.
назад | ОГЛАВЛЕНИЕ | вперед
| 
