|
назад | оглавление | вперед
1.2.5 Динамические характеристики АД при питании от
источника тока.
Основой для анализа динамических свойств АД может быть векторное уравнение ротора в синхронной системе
координат 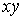 ,
если в нем ток ротора представить через ток статора ,
если в нем ток ротора представить через ток статора 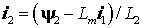 . Запишем это
уравнение в форме Коши . Запишем это
уравнение в форме Коши
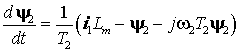 (1) (1)
и разделим составляющие векторов, совместив ось 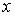 системы
координат с вектором системы
координат с вектором 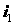 . Тогда с учетом . Тогда с учетом 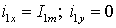 получим получим
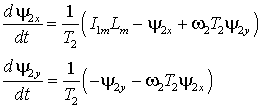 . (2) . (2)
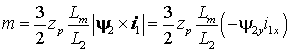 . . (3) (3)
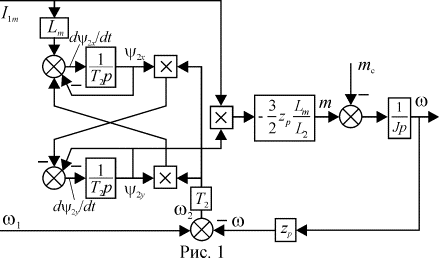
Структурная схема, соответствующая уравнениям (2-3)
совместно с уравнением движения 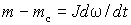 , представлена на рис. 1. Она имеет два
независимых управляющих входа: задания тока , представлена на рис. 1. Она имеет два
независимых управляющих входа: задания тока 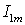 и частоты и частоты 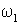 статора. Однако при
анализе тока намагничивания было отмечено, что нормальная работа двигателя
возможна только при введении функциональной связи
между каналом управления током и скольжением или скоростью вращения. Такую
связь, пользуясь понятием абсолютного скольжения статора. Однако при
анализе тока намагничивания было отмечено, что нормальная работа двигателя
возможна только при введении функциональной связи
между каналом управления током и скольжением или скоростью вращения. Такую
связь, пользуясь понятием абсолютного скольжения 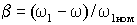 , можно представить функцией , можно представить функцией
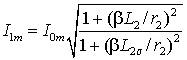 . .
При постоянном или медленно изменяющемся значении тока
статора 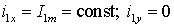 .
Заменим производную оператором Лапласа и представим уравнения (2) в виде .
Заменим производную оператором Лапласа и представим уравнения (2) в виде
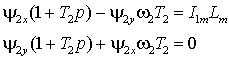 . .
Отсюда
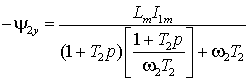 . .
Подставляя это выражение в уравнение момента (3), получим
уравнение динамической механической характеристики
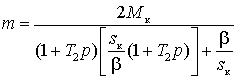 , (4) , (4)
где 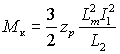 – критический момент; – критический момент; 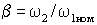 –
относительная частота ротора или абсолютное скольжение, а –
относительная частота ротора или абсолютное скольжение, а 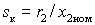 – критическое
скольжение при номинальной частоте статора. – критическое
скольжение при номинальной частоте статора.
Уравнение (4) формально идентично уравнению
динамической механической характеристики АД при питании от источника ЭДС.
Поэтому с ним можно проделать аналогичные преобразования и получить
линеаризованную механическую характеристику и передаточную функцию динамической
жесткости в виде
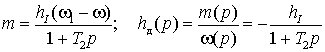 , ,
где 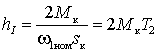 – модуль жесткости линеаризованной
механической характеристики. Жесткость этой – модуль жесткости линеаризованной
механической характеристики. Жесткость этой 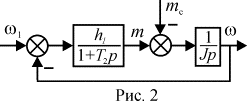 характеристики
существенно выше, чем характеристики АД с источником ЭДС. Их отношение
составляет характеристики
существенно выше, чем характеристики АД с источником ЭДС. Их отношение
составляет
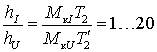 . .
Однако инерционность привода питающегося от источника тока
во много раз больше, т.к. 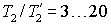 . В абсолютном исчислении постоянная
времени ротора составляет 0,15-1,5 с и большие значения относятся к двигателям
большей мощности. . В абсолютном исчислении постоянная
времени ротора составляет 0,15-1,5 с и большие значения относятся к двигателям
большей мощности.
назад | оглавление | вперед
| 
