Содержание
Предыдущий § Следующий

Глава двадцатая ЭЛЕКТРОДВИЖУЩИЕ СИЛЫ ОБМОТОК ПЕРЕМЕННОГО ТОКА

§ 20-1. Э. д. с. обмотки от основной гармоники магнитного поля

Общие замечания. В данной главе рассматриваются э. д .с, индуктируемые в обмотках переменного тока.

При конструировании машин переменного тока стремятся к тому, чтобы индуктируемые в обмотках э. д. с. были синусоидальными. Если э. д. с. индуктируются вращающимся магнитным полем, то для этого необходимр, чтобы распределение магнитной индукции вдоль воздушного зазора было также синусоидальным.

Получение вполне синусоидального распределения магнитного поля практически невозможно, однако для приближения к этой цели применяются различные меры конструктивного характера. Например, для улучшения кривой поля вЪзбуждения явнополюсных синхронных генераторов их полюсные наконечники (рис. 20-1) обычно выполняют с радиусом, несколько меньшим, чем радиус воздушного зазора, в результате чего величина зазора у края наконечника (8_т) больше, чем по его середине (б). На практике 6_m/S = 1 -т- 2 и коэффициент полюсного перекрытия а = Ь_р/х = = 0,60 -5- 0,75. Тем не менее и в этом случае кривая поля наряду с основной гармоникой (v = 1) содержит другие нечетные гармоники (v = 3, 5, 7 ...), амплитуды которых уменьшаются с увеличением их порядка v.

Вычислим сначала э. д. с, индуктируемую в обмотке основной пространственной гармоникой вращающегося поля (v = 1).

Э. д. с. проводника. Вращающееся со скоростью v = 2т/ синусоидальное магнитное поле индуктирует в каждом проводнике витка э. д. с.

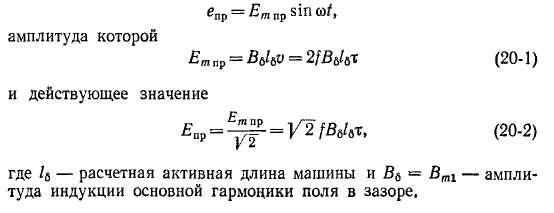
В ряде случаев как в синхронных, так и в асинхронных машинах для улучшения формы кривой э. д. с. обмотки (см. § 20-3) и для других целей (см. § 25-3) осуществляется скос пазов относительно

Рис. 20-1 Распределение магнитной

индукции поля возбуждения явнопо-

люсной синхронной машины вдоль

поверхности статора

Рис. 20-2. Э. д. с. проводника при скосе пазов

бегущего магнитного поля. Например, в явнополюсных синхронных машинах небольшой мощности иногда выполняют скос пазов статора относительно полюсных наконечников ротора или наоборот (см. также § 3-2). При этом фаза э. д. с, индуктируемых в отдельных участках проводника (рис. 20-2, б) синусоидально распределенным магнитным полем (рис. 20-2, а), беспрерывно изменяется вдоль проводника и элементарные э. д. с. АЕ, индуктируемые на обоих кон-цах проводника, сдвинуты по фазе на угол

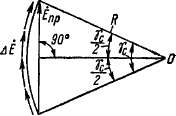Рис. 20-3. Определение

э. д. с. проводника при

наличии скоса пазов

где Ь_с — величина скоса.

В этом случае для определения э. д. с. проводника Е_пр необходимо сложить векторы э. д. с. отдельных участков проводника А£ (рис. 20-3). В пределе, если рассматривать бесконечно малые участки проводников, Д£' -*• 0 и геометрическая сумма i;_np векторов Д£ изобразится дугой и будет равна хорде окружности, опирающейся на Центральный угол Yc-

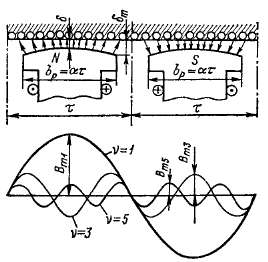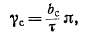
При отсутствии скоса А£ складываются арифметически и их сумма равна длине дуги на рис. 20-3. Отношение длины хорды на рис. 20-3 к ее дуге

определяет степень уменьшения э. д. с. £_пр при наличии скоса и называется коэффициентом скоса пазов обмот-к и. Подставив сюда приведенное выше значение угла у_с, получим

Очевидно, что при Ь_с -> 0 будет k_c = 1, Таким образом, в общем случае правую часть выражения (20-1) нужно умножить на k_c и, следовательно,

E_np = V2 fB_&hxk_c.                                                                                                                                                                                                                                                                                                                                                                                               (20-4)

Обычно скос относительно невелик и значение k_c близко к единице. Например, при bjx = 1/6

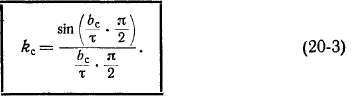т. е. э. д. с. Е_пр уменьшается на 1,1%.

Э. д. с. витка и катушки. Шаг витка и катушки обмотки переменного тока у по причинам, выясняемым ниже (см. § 20-3), чаще всего несколько укорачивают по сравнению с полюсным делением т (рис. 20-4), так что относительный шаг

P = Y                                       (20-5)

обычно меньше единицы.

Э. д. с. двух активных сторон витка £'_пр и £"_пр (рис. 20-4) имеют одинаковую величину, но сдвинуты по фазе на угол р"я (рис. 20-5), так как активные проводники витка сдвинуты в магнитном поле на такой угол. Э. д. с. витка равна геометрической разности э. д. с. проводников:

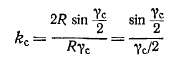
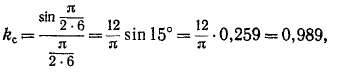
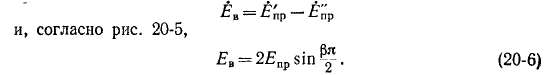
Входящая в выражение (20-6) величина

равна отношению геометрической суммы э. д. с. проводников витка Е_в к их арифметической сумме 2Е_пр, учитывает уменьшение э. д. с. витка в результате укорочения шага и называется к о э-ф -

фициентом укорочения шага обмотки. Очевидно, что величина Е_в максимальна при полном шаге (у = т, р = 1), когда k_y = 1.

Равенства (20-6) и (20-7) действительны также и при удлиненном шаге (у > т, р > 1).

Группа последовательно соединенных витков, уложенная в одни

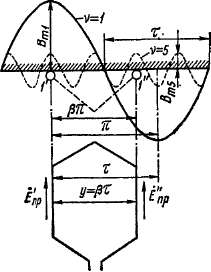Рис. 20-4. Э. д. с. проводников витка

Рис. 20-5. Определение э. д. с. витка

и те же пазы и имеющая, помимо изоляции отдельных витков, также общую пазовую изоляцию от стенок паза, называется катушкой. Если катушка содержит w_K витков, то э. д. с. катушки

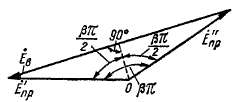
Э. д. с. катушечной группы. На рис. 19-5 и 19-6 были представлены обмотки простейшего вида, когда на каждую фазу под одним полюсом имеется только один паз. Обычно для получения достаточного количества проводников и витков в фазе и сохранения в то же время приемлемых размеров пазов количество пазов в машине делают больше. При этом ряд (q) катушек, имеющих по одинаковому количеству витков w_K и лежащих в соседних пазах, соединяют последовательно (рис. 20-6, где q — 4). Такую группу катушек, принадлежащих одной фазе, называют катушечной группой.

Э. д. с. соседних катушек группы сдвинуты на угол

(20-11)

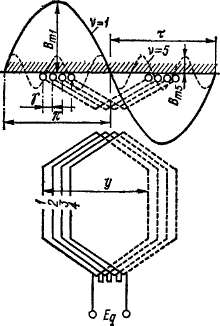соответственно сдвигу катушек относительно друг друга, в магнит--ном поле (рис. 20-7). При' этом вся группа из q катушек занимает по окружности якоря угол (электрический)

Рис. 20-6. Катушечная группа в магнитном поле

называемый углом фазной зоны.

Э. д. с. катушечной группы E_q равна геометрической сумме э. д. с. отдельных катушек группы (рис. 20-8) и меньше арифметической суммы э. д. с. этих катушек qE_K. Отношение

называется коэффициентом распределения обмотки и характеризует уменьшение э. д. с. катушечной группы вследствие распределения ее витков qw_K в q отдельных пазах. Таким образом, согласно выражению (20-13),

E_q = qE_Kk_p.                                     (20-14)

Вокруг фигуры рис. 20-8, образованной векторами £_к, можно описать окружность радиусом R. Тогда на основании этого рисунка

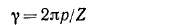
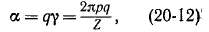
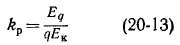
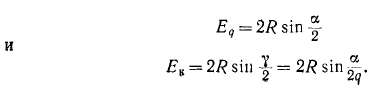
Подставив эти значения E_q и Е_& в (20-13), получим формулу для вычисления k_p:

Очевидно, что при q = 1 имеем k_p = 1, а при q > 1 будет k_p < 1.

Если в пределах угла фазной зоны а величину q увеличить,

переходя ко все более мелким пазам, то в идеализированном пре-

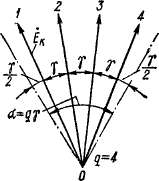
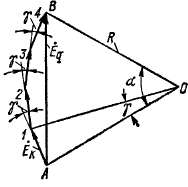Рис. 20-7. Э. д. с. катушек катушечной группы

Рис. 20-8. Определение э. д. с. катушечной группы

дельном случае, когда q = с», получим так называемую равномерно распределенную обмотку. Для такой обмотки, заменив в знаменателе (20-15) в связи с малостью угла синус его аргументом, получим

При q = оо ломаная линия АВ на рис. 20-8 превращается в дугу АВ описанной окружности, так как Е_к -»• 0. Отсюда следует, что выражение (20-16) вытекает также из рис. 20-8 как отношение хорды АВ к дуге АВ.

При заданном угле а величина k_poa является наименьшим значением fe_p. В реальных случаях, при 1 ==s q < оо, будет 1 S= k_p > &_р00,

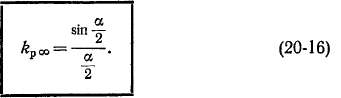
учитывает укорочение шага и распределение обмотки и называется обмоточным коэффициентом. Величину k_c также можно было бы ввести в качестве сомножителя в выражение для k_o6. Однако обычно этого не делают, так как скос влияет на величину э. д. с. лишь в том случае, когда пазы и проводники обмотки скошены относительно магнитного поля. Иногда же магнитное поле ориентировано вдоль скошенных пазов, и в этом случае скос на величину э. д. с. не влияет.

Э. д. с. фазы обмотки. В многополюсной машине каждая фаза обмотки содержит ряд катушечных групп, лежащих под разными полюсами (см. гл. 21). В наиболее распространенном случае все группы содержат одинаковое количество катушек q, занимают поэтому одинаковые углы а и сдвинуты относительно друг друга на целое число полюсных делений. В этом случае э. д. с. всех катушечных групп равны по величине и сдвинуты по фазе на 360° (при сдвиге групп на четное число т) или на 180° (при сдвиге на" нечетное число т). Такие катушечные группы можно соединить последовательно таким образом, что э. д. с. групп будут складываться арифметически. Возможно также их параллельное и смешанное соединение так, что э. д. с. всех параллельных ветвей будут одинаковы по величине и совпадут по фазе. Если в каждой ветви соединено последовательно п катушечных групп, то действующее значение э. д. с. каждой ветви и фазы обмотки в целом будет

представляет собой число последовательно соединенных витков каждой параллельной ветви и называется числом витков фазы.

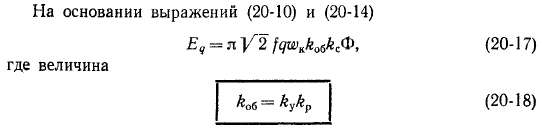
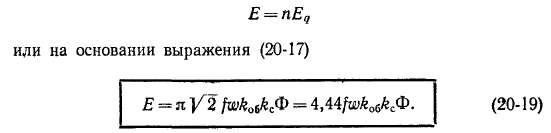
Если m-фазная обмотка заполняет все Z пазов и имеет а параллельных ветвей, то

где s_n — число эффективных проводников в пазу. Эффективный проводник может состоять из одного или некоторого числа параллельных проводников.

В более сложных случаях, когда отдельные катушечные группы состоят из различного количества катушек, также применима формула (20-19), если рассчитывать соответствующим образом коэффициент распределения обмотки k_p (см. § 21-2).

Выражение (20-19) отличается от выражения для э. д. с. обмотки трансформатора только наличием множителя k_o6k_c, который при Ь_с Ф 0, (3 Ф 1 и q > 1 меньше единицы. Это объясняется тем, что при Ь_с Ф 0 и р ф 1 поток полюса сцепляется с катушкой неполностью и при ^>1 в каждый момент времени потокосцепление различных катушек различно." Величина wk_o6 называется также эффективным числом витков обмотки.

Так как

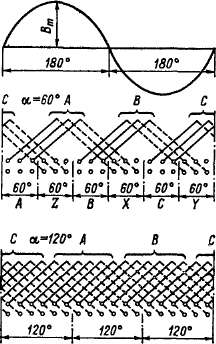Рис. 20-9. Принцип образования двухслойной трехфазной обмотки с фазными зонами а = 60° и а = 120°

А, В, С — основные фазные зоны; X, Y, Z — фазные зоны, в которых э д. с. проводников сдвинуты на 180° по отношению соответственно к зонам А, В, С

то из сопоставления этого выражения с равенством (20-19) следует, что амплитуда потокосцепления фазы обмотки

Э. д. с. трехфазной обмотки. Трехфазную обмотку конструируют таким образом, чтобы э. д. с. всех фаз были равны по величине и сдвинуты по фазе на 120°. Такую обмотку называют симметричной. Пространство машины используется в наибольшей степени, когда все Z пазов машины заняты обмоткой. Очевидно, что в симметричной обмотке Zlm = ц. ч.

Симметричную трехфазную обмотку с одинаковыми катушечными группами можно выполнить с фазными зонами а = 60° и а = 120°

(рис. 20-9). Очевидно, что обмотка с зоной 60° выгоднее, так как в этом случае векторы э. д. с. катушек группы занимают меньший угол (см. рис. 20-7) и их геометрическая сумма отличается от их арифметической суммы меньше (см. рис. 20-8), чем при а = 120°. В частности, для равномерно распределенной обмотки с зоной а = 60° или а = я/3, согласно выражению (20-16),

т. е. при а = 120° э. д. с. в 0,955 : 0,828 =1,15 раза меньше и для получения такой же э. д. с, как и при а = 60°, количество витков и меди необходимо увеличить на 15%.

Вследствие сказанного на практике предпочитают применять трехфазные обмотки с зоной 60°, а обмотки с зоной 120° исполь^ зуют в особых случаях. Очевидно, что соединенная с коллектором обмотка якоря трехфазной коллекторной машины (см. рис. 19-21)| имеет а = 120°. По числу фазных зон на протяжении 2т обмотвд с зоной 60° называются также шестизонными, а с зоной 120° — трех-¹ зонными.

В общем случае m-фазную обмотку (m S= 3) также можно выпол-i нить с двумя различными фазными зонами:

В первом случае на протяжении 2т имеется 2пг фазных зон (2т-зонная обмотка), а во втором — m зон (/и-зонная обмотка). Очевидно»» что первый случай более выгоден и для него, согласно выражению (20-15),

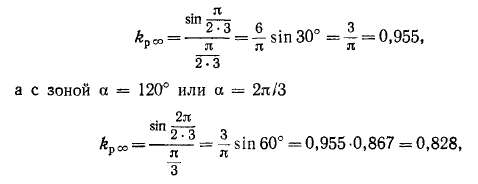
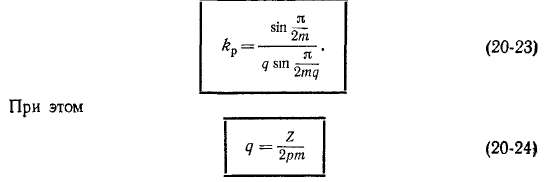
представляет собой число пазов на полюс и фазу, а выражение (20-21) можно записать также в следующем виде:

Значения коэффициентов распределения обмотки для трехфазных обмоток с фазной зоной 60° для основной гармоники (v = 1) и высших гармоник приведены в табл. 20-1.

Таблица 20-1 Коэффициенты распределения ft_pv шестизонных трехфазных обмоток

Э. д. с. двухфазной обмотки. В машинах специального назначения нередко применяются двухфазные обмотки (т = 2), в которых э. д. с. фаз сдвинуты на 90°. Такие обмотки также выполняются с заполнением всех пазов (см. рис. 21-20), и фазная зона а = 90^й. При этом для k_p и q пригодны формулы (20-23) и (20-24).

Э. д. с. однофазной обмотки. Обмотку однофазной машины можно выполнить с заполнением всех пазов машины. Катушечная

группа, или фазная зона, при этом занимает целое полюсное деление и а — 180° или а = я, причем, согласно выражению (20-16),

Таким образом, в этом случае коэффициент k_p мал, так как складываются векторы э. д. с. катушек, занимающие большой угол (см. рис. 20-7 и 20-8). Это невыгодно, и поэтому обычно применяют однофазные обмотки, заполняющие две. трети пазов машины. При

о                                                       О

этом фазная зона занимает ^тиа= 120° или а = ^я. В данном случае в соответствии с выражением (20-16)

и для получения одинаковых э. д. с. потребуется в 0,828 : 0,637 = = 1,32 раза меньше активных проводников или витков.

Соотношения, приведенные выше, действительны также в случае, когда синусоидально распределенное магнитное поле неподвижно относительно обмотки, но изменяется во времени или пульсирует по синусоидальному закону с частотой f.

§ 20-2. Э. д. с. обмотки от высших гармоник магнитного поля

Полученные в § 20-1 выражения нетрудно распространить на э. д. с. E_v, индуктируемую в обмотке высшей пространственной гармоникой магнитного поля (см. рис. 20-1). Действительно, полюсное деление v-гармоники t_v в v раз меньше т, и поэтому, если сдвиг двух проводников витка относительно основной гармоники (v = 1) составляет угол (Зя, то относительно v-й гармоники этот сдвиг равен \$п (см. рис. 20-4). В результате при определении коэффициента укорочения для v-й гармоники'вместо выражения (20-7) надо пользоваться равенством

Сдвиг фаз э. д. с. соседних катушек группы также будет в v раз больше (см. рис. 20-6, 20-7 и 20-8), и поэтому

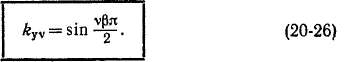
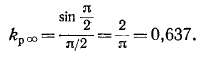
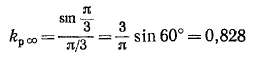
коэффициент распределения надо вычислять не по (20-15) и (20-23), а по формулам:

Аналогично угол скоса паза относительно поля v-й гармоники (см. рис. 20-2) также будет в v раз больше, и поэтому вместо выражения (20-3) для коэффициента скоса получим

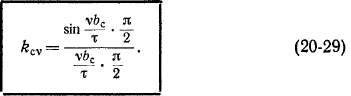Обмоточный коэффициент для высшей гармоники

Отдельные сомножители k_o(i, k_C4 и произведение k_o6ji^ в целом при вычислениях по приведенным формулам могут получиться отрицательными. Это будет означать поворот фазы E_v на 180° по сравнению со случаем, когда произведение k_o64k_c, положительно.

Вместо выражения (20-19) для э. д. с. фазы от высшей гармоники поля будем иметь

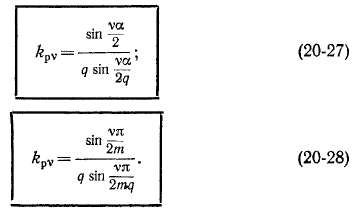
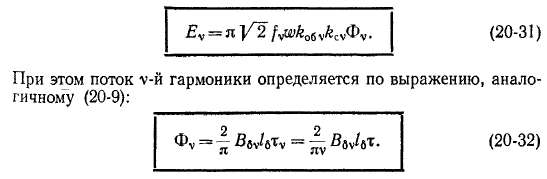
Здесь принято во внимание, что полюсное деление для v-й гармоники x_v в v раз меньше полюсного деления основной гармоники.

Частота э. д. с. от высшей гармоники поля Д, зависит от скорости вращения этой гармоники. Например, все гармоники поля возбуждения синхронной машины (см. рис. 20-1) вращаются со скоростью вращения полюсов, т. е. с одинаковой скоростью. Однако число полюсов v-й гармоники в v раз больше, и поэтому в данном случае fv — v/, т. е. высшие гармоники поля индуктируют э. д. с. высших частот или высшие гармоники э. д. с. В других случаях все э. д. с. E_v могут иметь одинаковую частоту (см. § 23-2).

Если э. д. с. от различных гармоник поля имеют различные частоты, то действующее значение суммарной, или полной, э. д. с.

§ 20-3. Улучшение формы кривой э. д. с.

Постановка вопроса. Если, как, например, в синхронных машинах высшие пространственные гармоники поля возбуждения индуктируют в обмотке высшие временные гармоники э. д. с, то полная э. д. с. обмотки будет изменяться во времени несинусоидально.

Как уже указывалось (см. § 13-1), высшие гармоники э. д. с. могут вызвать в электрических сетях и приемниках ряд нежелательных явлений. Поэтому необходимо принять меры к их подавлению. Первой из таких мер является улучшение формы кривой распределения самого магнитного поля и ее приближение к синусоидальной. Такая мера в отношении явнополюсной синхронной машины рассматривалась в начале §20-1. Однако получить вполне приемлемые результаты при этом не удается.

Поэтому стремятся подавлять высшие гармоники э. д. с. с помощью соответствующей конструкции обмоток. К таким конструктивным мерам относятся: 1) укорочение шага обмотки; 2) распределение обмотки по пазам таким образом, чтобы число катушек в катушечной группе было q > 1; 3) скос пазов обмотки.

Рассмотрим этот вопрос подробнее.

Э. д. с. от третьей гармоники поля. Три фазы обмотки А, В, С сдвинуты относительно друг друга по отношению к гармонике поля v = 1 на 120°, по отношению к гармонике v = 3 на 3-120° = = 360° или 0°, по отношению к гармонике v = 5 на 5 -120° = 600° или 240°, по отношению к гармонике v = 7 на 7-120° = 840° или 120° и т. д. (рис. 20-10). На такие же углы сдвинуты соответствующие гармоники э. д. с. этих фаз. Таким образом, э. д. с. гармоник v = 3 и кратных им (v = 9, 15, 21 и т. д.) в разных фазах обмотки совпадают по фазе и поэтому при соединении обмотки в звезду

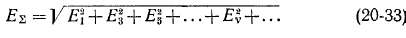
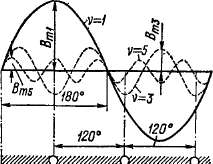ABC Рис. 20-10. Положение пространственных гармоник поля относительно отдельных фаз трехфазной обмотки

(рис. 20-11, а) в линейных напряжениях эти гармоники будут отсутствовать. При соединении обмотки в треугольник (рис. 20-11, б) _э. д. с. гармоник v = 3 складываются, вызывают ток третьей гармоники г₃, циркулирующий по замкнутому треугольнику, и расходуются на падения напряжения внутри обмотки. Поэтому и в данном случае линейные напряжения не содержат третьих гармоник,

Отметим, что соединения обмотки в треугольник стремятся избегать, так как появляющиеся при этом третьи гармоники тока вызывают излишние потери и нагрев обмоток. Кроме того, в однофазных обмотках с фазной зоной а = 120° э. д, с. гармоник v = 3, 9, 15 ... всегда равна нулю, так как на основании выражения (20-27) для этих гармоник k_pV = 0.

По изложенным причинам при конструировании обмоток обычно необходимо заботиться об уменьшении влияния гармоник, не кратных трем.

Укорочение шага обмотки. При Р = 1, согласно формуле (20-26), для всех нечетных гармоник k_yv = ±1, т. е. в э. д. с. витка э. д. с. всех гармоник проявляются в полной мере. Однако соответствующим выбором шага обмотки можно в принципе добиться уничтожения любой определенной гармоники э. д. с. Например, если сократить.

шаг на 1/5 полюсного деления, то Р = 4/5, в соответствии с формулой (20-26) для v = 5

k_yv — sin . ■ = sin 2я = 0

и поэтому также Е_ь = 0. Такой результат объясняется тем, что при указанном укорочении шага э. д. с. от 5-й гармоники поля в двух активных проводниках витка совпадают по фазе и в контуре

витка действуют встречно друг другу (см. рис. 20-4). Такого же результата можно достичь, если взять р = 6/5, однако удлинение шага невыгодно, так как в большинстве случаев это вызывает увеличение расхода обмоточного провода.

Если желательно уничтожить 7-ю гармонику, то следует укоротить шаг на 1/7 полюсного деления, т. е. взять р = 6/7 и-т. д.

Достичь одновременного уничтожения всех гармоник невозможно. Поэтому следует стремиться к наибольшему ослаблению

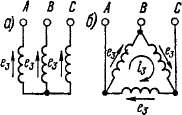Рис. 20-11. Третьи гармоники э. д. с. в трехфазной обмотке.

т. е. основная гармоника э. д. с. уменьшается незначительно.

Укорочение шага возможно только на целое число зубцовых делений. Поэтому не всегда можно иметь |J = 5/6 и обычно берут р = 0,80 -н 0,86.

Распределение обмотки. При q — 1, согласно выражениям (20-27) и (20-28), для всех гармоник k_pV = ±1 и поэтому ослабления гармоник э. д. с. в обмотке за счет ее распределения в пазах не происходит. Однако если q > 1, то для многих гармоник | k_pV | < k_pl (см. табл. 20-1) и э. д. с. соответствующих гармоник значительно уменьшаются. Это объясняется тем, что э. д. с. катушек катушечной группы для v-й гармоники сдвинуты на углы vy вместо углов Y для v = 1 (см. рис. 20--6, 20-7 и 20-8), в результате чего эти э. д. с. складываются под большими углами и их сумма уменьшается. В то же время, как видно из табл. 20-1, для v = 1 значения k_pl = k_p близки к единице, т. е. распределение обмотки мало влияет на основную гармонику э. д. с.

Гармоники зубцового порядка и скос пазов. Из табл. 20-1 видно также, что и при q > 1 для ряда гармоник k_pV = ±k_pl (числа, выделенные жирным шрифтом), т. е. ослабления э. д. с. этих гармоник не происходит. Такие гармоники v = v_z называются гармониками зубцового поряд к_а. Их порядок

где k = 1, 2, 3, ..., при k = 1 близок к количеству зубцов на пару полюсов Zip, чем и обусловлено их название. Для трехфазной обмотки

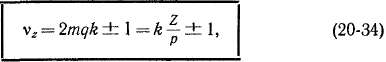
Например, при q = 2, согласно равенству (20-35), v_z = 11, 13, 23, 25 ... При q = 1 все гармоники v = 5, 7, 11, 13 ... являются гармониками зубцового порядка.

В поле возбуждения синхронной машины содержатся все гармоники порядка v_z. Угол сдвига проводников у двух соседних пазов для основной гармоники поля определяется равенством (20-11). Для э. д. с. от v_z-& гармоники поля этот угол в v^ раз больше, и на основании выражений (20-11) и (20-34)

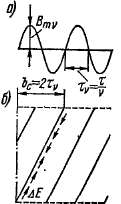что эквивалентно углу ±у. Таким образом, э. д. с. проводников отдельных пазов от v^-й гармоники поля сдвинуты относительно друг друга на такие же углы, как и э. д. с. от основной гармоники поля. Поэтому векторы этих э. д. с. складываются в контуре витка и в катушечной группе под одинаковыми углами сдвига фаз. В связи с этим не только коэффициенты распределения, но и коэффициенты укорочения шага для гармоник v = 1 и v = v_z одинаковы. Таким образом, укорочением шага обмотки и выбором целого числа q > 1 нельзя достичь уничтожения или ослабления высших гармоник э. д. с. от гармоник поля зубцового порядка. Однако при увеличении q увеличивается порядок гармоник \_г, и поскольку гармоники высших порядков в кривой поля выражены слабее, то увеличение q все же способствует улучшению формы кривой э. д. с. обмотки. Уменьшение высших гармоник э. д. с, в частности, от гармоник поля зубцового порядка возможно также осуществлением скоса пазов или полюсных наконечников. Если, например, выбрать величину скоса

5

Рис. 20-12. Случай,

когда при скосе

пазов E_v = 0

то, согласно выражению (20-29), &_Cv = 0 и по формуле (20-31) £„ = 0. Физически это объясняется тем, что при этом в отдельных участках проводника индуктируются одинаковые по величине и обратные по направлению э. д. с. (рис. 20-12).

Наиболее сильными являются первые гармоники зубцового порядка, для которых в выражениях (20-34) и (20-35) k = 1. Э. д. с. одной из этих гармоник будет равна нулю, если взять

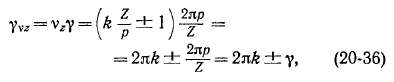
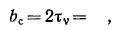
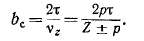
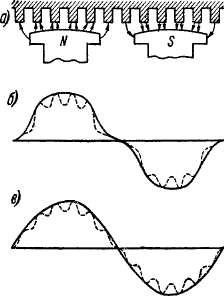На практике обычно величину скоса берут равной зубцовому делению:

и тогда э. д. с. от всех гармоник зубцового порядка будут значительно ослаблены.

Влияние пазов. Рассмотрим влияние пазов статора на кривую поля возбуждения синхронной машины и на э. д. с. обмотки статора.

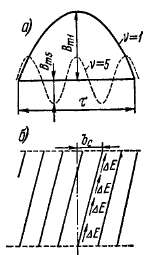
На рис. 20-13, а схематически изображены полюсы синхронной машины и ее статор с пазами при Zip — 6. На рис. 20-13, б показан характер кривой распределения магнитной индукции поля возбуждения полюсов при отсутствии (сплошная линия) и при наличии (штриховая линия) пазов. На рис. 20-13, в представлены такие же кривые для случая, когда кривая поля возбуждения при отсутствии пазов содержит только основную гармонику.

Как следует из рис. 20-13, пазы искажают кривую поля. Можно представить себе, что наличие пазов и зубцов вызывает ряд дополнительных гармоник поля, которые накладываются на первоначальную кривую поля и могут быть названы зубцовыми гармониками поля.

Если первоначальное поле синусоидально (рис. 20-13, е), то при наличии пазов возникают дополнительные вращающиеся гармоники поля, имеющие порядок

Рис 20-13 Форма кривой поля

возбуждения синхронной машины

при наличии пазов на статоре

Эти гармоники содержат в v_s раз больше полюсов, чем основная гармоника, но вращаются, как можно показать, также с v_s раз меньшей скоростью и поэтому индуктируют в обмотке статора э. д. с. основной частоты.

Таким образом, если поле возбуждения при отсутствии пазов синусоидально, то наличие пазов, несмотря на искажение кривой поля, не приводит к искажению кривой э. д. с. Искажение кривой э. д. с. связано только с наличием высших гармоник в первоначальной кривой поля (сплошная линия на рис. 20-13, б). Более

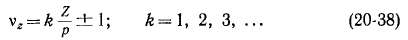
подробный анализ этого вопроса показывает, что при Zip, равном целому четному числу, наличие пазов вызывает многократное увеличение тех высших гармоник э. д. с, которые индуктируются нечетными гармониками поля зубцового порядка v_z [см. равенство (20-34)], содержащимися в первоначальной кривой поля. В этом и заключается вредное влияние пазов на форму кривой э. д. с. При Zip, равном целому четному числу, эффективной мерой борьбы с этим влиянием является скос пазов или полюсных наконечников. При Zip, не равном целому четному числу, получаются так называемые дробные обмотки (см. § 21-2), которые обеспечивают хорошую форму кривой э. д. с.

Содержание
Предыдущий § Следующий