Содержание
Предыдущий § Следующий

2 Магнитная система и ее расчет

Целью магнитных расчетов является установление количественной зависимости магнитного потока от тока возбуждения, а также определение магнитной индукции в отдельных частях машины, что необходимо для анализа свойств машины.

2.1. Устройство магнитной системы и принципы ее расчета

Магнитный поток в электрических машинах возникает из-за наличия тока в обмотках: в машинах постоянного тока и синхронных по обмоткам возбуждения проходит постоянный ток, по обмоткам якоря — переменный; в асинхронных машинах и трансформаторах по всем обмоткам проходит переменный ток. В малых машинах постоянного тока и синхронных иногда применяются постоянные магниты.

Для улучшения магнитной связи между обмотками и увеличения магнитного потока магнитная система машин выполняется из ферромагнитных материалов, обладающих хорошей магнитной проницаемостью. В большинстве случаев применяется электротехническая сталь, легированная кремнием (1 ...5,0%) и другими присадками, уменьшающими потери в переменном магнитном поле. Иногда применяется литая сталь, чугун, а иногда, в очень малых машинах, пермаллой и феррит.

Основной магнитный поток замыкается по стали (рис. 2.1) и через воздушный зазор между статором и ротором; потоки рассеяния замыкаются в междуполюсном пространстве и вокруг проводников, лежащих в пазах.

Цель расчета магнитной системы — установление связи между магнитным потоком и токами в обмотках машины. Кроме того, представляет интерес плотность магнитного потока — магнитная

индукция — в воздушном зазоре машины и других частях магнито-провода.

Основные положения расчета магнитной системы. Методы расчета базируются на уравнениях Максвелла.

Магнитный поток, пронизывающий замкнутую поверхность, всегда равен нулю:

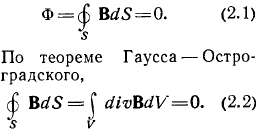Так как интегрирование ведется по объему конечной величины, а равенство интеграла нулю сохраняется при любом значении этого объема, подынтегральное выражение должно быть равно нулю:

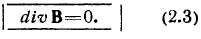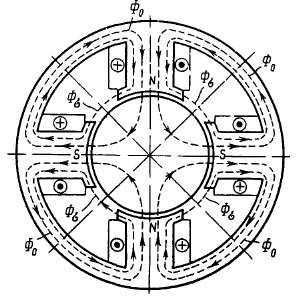Рис. 2.1. Магнитный поток в четырех-полюсной машине

Это означает, что магнитная индукция не имеет дивергенции, т. е. не имеет ни источ-

ников, ни стоков. Линии магнитной индукции всегда непрерывны и образуют замкнутые петли; они нигде не начинаются и нигде не заканчиваются. Уравнение (2.3) называется уравнением непрерывности.

Магнитная индукция в некоторой точке связана с напряженностью магнитного поля соотношением

где \л — магнитная проницаемость вещества.

Напряженность поля связана с плотностью тока выражениями:

Согласно (2.6) циркуляция вектора напряженности (интеграл по замкнутому контуру) равна полному току, проходящему через поверхность, охваченную циркуляцией. Это равенство называется законом полного тока.

Интеграл напряженности по части пути от U до /₂

где ф1 и фг — скалярные магнитные потенциалы в точках / и 2, а Fi2 — магнитное напряжение между точками 1 и 2.

Часто полный ток называют магнитодвижущей силой (МДС) или намагничивающей силой по аналогии с электродвижущей силой. Магнитные напряжения участков называются составляющими МДС.

Закон Ома магнитной цепи. При практических расчетах уравнение (2.6) принимает вид

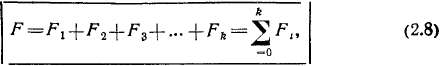где F = <£ НсИ=2/ — МДС; F_it F₂,... ,F_k — магнитные напряжения однородных участков магнитопровода.

Магнитная цепь машины разбивается на следующие однородные участки, для каждого из которых определяется магнитное напряжение: F_e — магнитное напряжение воздушного зазора; Fzi — зубцового слоя статора; F_Zi — зубцового слоя ротора; F_a — сердечника ротора; F] — ярма статора; F_m — сердечников электромагнитов.

С учетом (2.8)

В уравнениях машин конкретных видов отсутствуют некоторые члены правой части: в машинах постоянного тока часто нет зубцового слоя на статоре, в синхронных с явновыраженными полюсами— зубцов на роторе, а с неявновыраженными полюсами — сердечников электромагнитов, как и в асинхронных машинах. Однако эти различия несущественны и могут быть легко учтены в каждом конкретном случае.

В многополюсных машинах (см. рис. 2.1), в силу симметрии, можно подсчитать магнитное напряжение только для одного из параллельных контуров замыкания магнитного потока, т. е. определить поток, сцепленный с обмотками двух соседних полюсов (расчет на пару полюсов).

Магнитное напряжение каждого из последовательно включенных участков

где Я, — среднее значение напряженности на данном участке; /,— средняя длина магнитной линии данного участка.

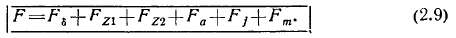
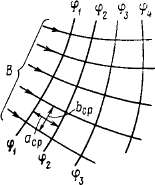Рис 2 2 Картина маг нитного поля

Формула (2 13) называется законом Ома магнитной цепи и полностью тождественна закону Ома электрической цепи Однако практическое использование этой формулы ограничено качественным рассмотрением процессов

Для количественных расчетов формула (2 13) неудобна по двум причинам 1) магнитное сопротивление стальных участков магнитопровода — переменная величина, так как магнитная проницаемость стали зависит от индукции в ней, 2) участки магнитопровода машин обычно имеют ширину, соизмеримую с длиной, что затрудняет определение расчетных значений площади поперечного сечения и средней длины магнитной линии

Первое затруднение — непостоянство \i —

решается сравнительно просто магнитные расчеты ведут, задаваясь известным значением магнитного потока, затем находят индукцию, по индукции — магнитную проницаемость, затем — напряженность магнитного поля и магнитное напряжение

То обстоятельство, что начинать расчет, задаваясь магнитным напряжением, невозможно, не вызывает сложностей на практике

Главная трудность заключается в построении картины поля, по которой определяются площадь расчетного сечения и средняя длина магнитной линии

Картина магнитного поля. Картина поля (рис 2 2)—графическое изображение магнитного поля в пространстве На ней показаны линии направления магнитной индукции и линии уровня (эквипотенциальные линии), связывающие между собой точки с одинаковым скалярным магнитным потенциалом Эти линии пересекаются между собой под прямым углом, так как в точке пересечения не может быть составляющей индукции, совпадающей с эквипотенциальной линией

Поскольку линии индукции, по определению, не могут пересекаться между собой, магнитный поток, ограниченный двумя линиями индукции, неизменен на всем их протяжении Его значение

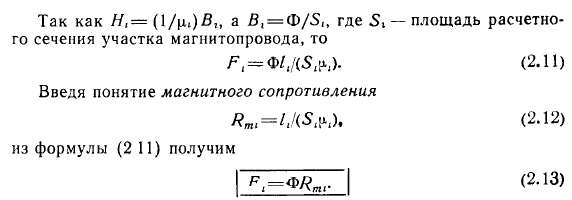
а все пространство, в котором существует магнитное поле, оказывается разбитым на криволинейные квадраты

Построенная таким образом картина поля дает наглядное представление о магнитном поле

Сгущение магнитных линий указывает на увеличение индукции, определяемой как В_ср=АФ/(Ь_Ср1а), подразделяя крупные квадраты на множество мелких, можно достаточно точно определить распределение индукции по любой интересующей поверхности

Абсолютное значение потока трубки, к которой приложена разность потенциалов (магнитное напряжение), определяется из условия

где /"/т=Д<р — разность потенциалов между соседними эквипотенциальными поверхностями, m — число последовательно соединенных звеньев трубки

Поток, замыкающийся через рассматриваемую поверхность,

где п — число трубок, замыкающихся через данную поверхность Если п не целое число, то в (2 20) подставляют дробное число Для более точного определения числа трубок в этом случае исходная единичная трубка разбивается на частичные трубки, сначала пополам, потом на четыре части и т д Поле частичных трубок тоже образует криволинейные квадраты, если одновременно с делением единичной трубки производить соответствующее дробление и

потенциалов, проводя линии уровня, соответствующие 0,5Дф, 0,25Дф и т. д.

Магнитное сопротивление участка можно определить по формуле

хотя чаще по картине поля определяются расчетные площадь поперечного сечения S, и средняя длина магнитной линии /,.

Обычно значение одной величины, например 5,, определяется «на глаз», а второй—из формулы (2.12):

/, = /?А,.                                                                                                                                                                                                                                                                                                                                                                                                                                                                           (2.22)

Таким образом, картина поля не только наглядна, но и дает исчерпывающую количественную характеристику магнитного поля.

Построение картины поля сводится к решению уравнения Лапласа

если в пространстве отсутствуют проводники с током, и к решению уравнения Пуассона

если проводники с током имеются.

Аналитические решения этих уравнений известны только для частных случаев (полуплоскости, круга, кольца и некоторых других) и обычно картина поля определяется приближенно.

Графический метод построения картины поля заключается в том, что линии индукции и уровня рисуются так, чтобы все пространство было разбито на криволинейные квадраты.

Перед построением картины поля должны быть заданы значения потенциала на границах области. Для облегчения построения придерживаются следующих правил:

начинать построение с тех мест, где направление линии индукции наиболее достоверно: рассчитано каким-то другим методом, известно из-за симметрии поля и т. д.;

начинать построение там, где ожидается большое значение индукции;

строго следить, чтобы линии индукции и уровня пересекались под прямым углом; это относится и к хорошо проводящим поток граничным поверхностям: например, сталь, ограничивающая поле в воздухе, должна приниматься за эквипотенциальную поверхность и линии индукции должны выходить из стали и входить в нее под углом 90°.

Все сказанное ранее относилось к безвихревому полю. Если в рассматриваемой области расположены проводники с током, то задача построения поля усложняется. Обычно область, занятая то-

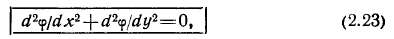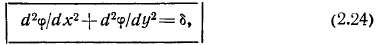
ком, представляется в виде тонкого слоя с той же результирующей МДС. В этом случае на поверхности с токовым слоем меняется скалярный магнитный потенциал, а остальное построение такое же, как при безвихревом поле.

Построение картины поля при постоянном и переменном токах возбуждения одинаково. При переменном токе расчет обычно ведется по амплитудным значениям.

Графическое построение поля требует опыта и искусства расчетчика. Обычно погрешность рас-чета полей простых форм составляет 5... 10%. Метод конечных разностей (метод потенциаль-ной сетки) для расчета поля так же универсален, как и метод графического построения картины поля, но не требует от расчетчика большого искусства и интуиции.

На рассчитываемую область накладывается мелкая сетка с квадратными ячейками. Стороны квадратов — h, как на рис. 2.3.

Рассмотрим точку 0 с потенциалом фо. По оси х рядом с этой точкой расположены точки \R и S, а по оси у—Р и Q.

Рис. 2.3. Элемент потенциальной сетки

Потенциал соседних точек можно выразить через потенциал и соответствующие приращения

(2.29)

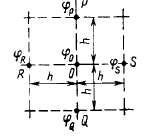
Уравнение в разностной форме должно удовлетворяться для каждой точки внутри области. Если имеется N точек, то такие уравнения для каждой из них составляют систему уравнений с N неизвестными.

Обычно задается потенциал на границе области и, таким образом, решение краевой задачи разностным методом сводится просто к решению системы линейных уравнений, правда, с огромным числом неизвестных.

Решать системы уравнений целесообразно методом итераций. Сначала задаются во всех внутренних точках сетки приближенными значениями скалярного потенциала (приближения могут быть очень грубыми) и обозначают эти значения системой № 1. Затем, используя данные системы № 1, определяют значения потенциала всех точек по формуле

и образуют новую систему № 2. Из системы № 2 образуют таким же образом систему № 3 и т. д. Процесс итерации заканчивается, когда в пределах заданной точности система N_n+i совпадает с системой N_n- Математически доказано, что описанный процесс будет сходящимся.

В безвихревом потенциальном поле максимальное и минимальное значения функции внутри области не могут превосходить максимального и минимального значений функции на границах области. Поэтому при расчете на ЭВМ бывает удобно принять минимальный потенциал на границе области за нулевой уровень и всем узловым точкам внутри области задать нулевые значения. Этот прием экономит время при составлении программы, а увеличение времени машинного счета, из-за необходимости проведения нескольких лишних итераций, ничтожно. Потенциальную сетку следует накладывать на исследуемую область так, чтобы возможно большая часть линий, ограничивающих область, совпадала с узловыми точками потенциальной сетки. Если совпадения точек нет, то приходится заданный на границе потенциал экстраполировать в узловые точки сетки, ближайшие к границе, и считать потенциал этих точек в процессе итерации неизменным. Чтобы уменьшить погрешность, иногда приходиться вблизи границы делать мелкую сетку или даже переходить к другой системе координат, например к системе полярных координат.

При ручном счете желательно как можно точнее определить начальное значение потенциалов внутри области, так как при сложной форме области сходимость итерационного процесса иногда бывает очень медленной.

Сначала для приближенного определения потенциалов внутри области можно, например, построить картину поля графически, методом криволинейных квадратов, а потом уточнять с помощью сетки. Часто на первом этапе применяют грубую сетку, а затем — мелкую. Имеется и ряд других приемов ускорения расчета.

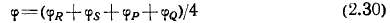
На рис. 2.4 показано распределение скалярного потенциала в воздушном зазоре и пазу якоря, определенное методом потенциальной сетки.

После расчета потенциалов в магнитном поле построение картины поля не вызывает затруднений; как указывалось выше, это целесообразно сделать для наглядности и простоты определения проводимости участка.

Некоторое распространение имел в недавнем прошлом метод моделирования магнитного поля с помощью электропроводной бумаги или тонкой фольги, наклеенной на толстую бумагу. Из бумаги вырезается фигура, в масштабе повторяющая исследуемую область. Магнитный потенциал заменяется электрическим, который подводится к границам с помощью медных электродов, окаймляющих область. Распределение электрического потенциала, пропорционального магнитному, определяется с помощью вольтметра с малым потреблением тока. В настоящее время этот метод применяется очень редко, так как имеет значительно большую трудоемкость и меньшую точность, чем расчет на ЭВМ.

Имеется и ряд других, менее распространенных методов расчета магнитного поля [9].

Содержание
Предыдущий § Следующий