Содержание
Предыдущий § Следующий

2.3. Магнитное напряжение зубцового слоя

Площадь сечения зубцов меньше площадей сечения других чйс-тей магнитопровода, поэтому индукция в зубцах больше индукйии в других частях.

В зубцах с параллельными стенками (см. рис. 2.9, б) магнитные линии идут параллельно друг другу, поэтому индукция по высоте зубца неизменна:

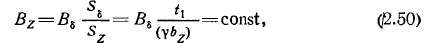где у—0.9..Д93 — коэффициент заполнения объема якоря сталью, учитывающий наличие изоляции между листами и волнис/гость стали.

В клиновидных зубцах пазы имеют параллельные стенки (см. рис. 2.9, б) и площадь поперечного сечения зубца изменяется по высоте:

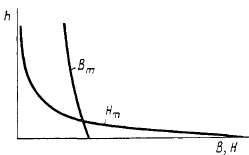
На рис. 2.11 приведена диаграмма изменения индукции по высоте зубца при v=l,5, а также кривая изменения напряженности магнитного поля в зубце, полученная из кривой намагничивания электротехнической стали марки 1212, при fizmin=l,6 Тл. Из рис. 2.11 видно, что напряженность магнитного поля в зубце неравномерна.

Магнитное напряжение в зубце

Из-за сложного характера изменения магнитной проницаемости электротехнической стали при изменении индукции нужно вычислять магнитное напряжение в зубце в каждом конкретном случае с помощью методов численного интегрирования, что требует трудоемких расчетов даже при применении современных вычислительных средств.

Для ориентировочных расчетов часто применяется метод расчета по эквивалентной напряженности поля в сечении, расположенном йа Уз высоты зубца от его основания. В этом сечении индукция

Из кривых намагничивания или таблиц определяется напряженность магнитного поля H_zi/3 и магнитное напряжение зубцового слоя

а если на пару полюсов, то вдвое больше, так как поток дважды замыкается через зубцовый слой:

Рис. 2.11. Изменение магнитной индукции и напряженности магнитного поля по высоте зубца

На рис. 2.12 приведены кривые намагничивания зубцового слоя при v=l,5, построенные способом точного численного интегрирования уравнения (2.55) (сплошная линия на рисунке) и по индукции в сечении на 7з высоты от основания (пунктирная линия). Для распространенных конфигураций зубцового слоя этот метод дает погрешность до 10% в значении индукции и до 45% в значении магнитного напряжения.

Более подробные исследования показали, что рассмотренный метод имел бы строгое обоснование, если бы кривую намагничивания стали можно было выразить формулой

однако зависимость напряженности поля от индукции имеет более сложный характер.

Меньшую погрешность, особенно при больших значениях индукции в зубце, дает метод расчета по трем сечениям:

где #mim Н_ср и Я_тах — соответственно напряженности поля в головке, в среднем сечении и в ножке зубца.

Было установлено, что погрешность в определении расчетной напряженности поля методом трех сечений значительно меньше,

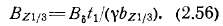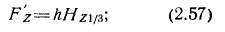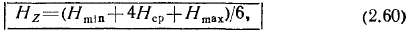
чем в методе расчета по напряженности на высоте '/з от основания зубца; практически расчет по (2.60) совпадает с точным интегрированием.

При напряженности поля в зубцах более 1,8 Тл нужно учитывать проводимость паза.

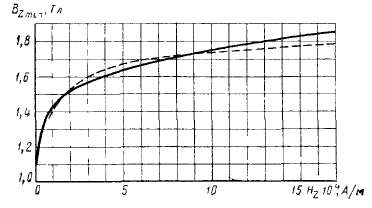Рис. 2.12. Кривые намагничивания зубцового слоя

Поток зубцового деления Ф< из-за насыщения зубцов разделяется на две части (рис. 2.13, а), одна из которых — Ф_г — проходит через зубец, а вторая — Ф_п — через паз:

B_Zx — расчетную индукцию. Повторяя эту операцию несколько раз, можно построить зависимость B_z=f(H_z) при заданном значении k_z.

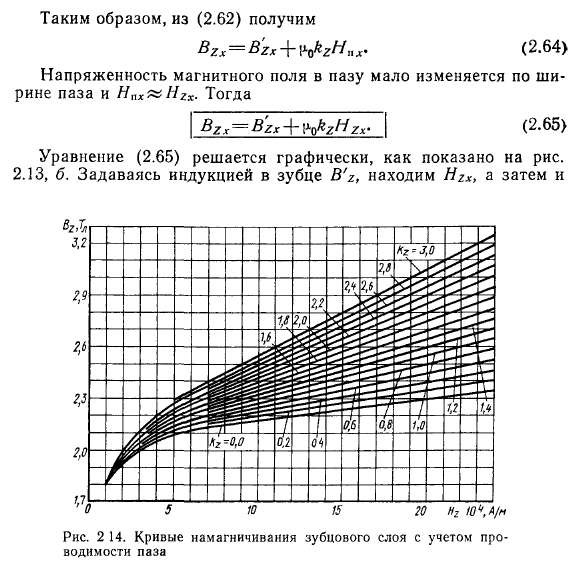
На рис. 2.14 показано семейство кривых B_z=f(H_z), построенных описанным выше способом, для стали марки 1212, при всех встречающихся на практике значениях k_z с учетом проводимости паза.

Расчет магнитного напряжения зубцового слоя с учетом проводимости паза производится так же, как и без учета этой проводимости, но напряженность магнитного поля определяется по диаграмме рис. 2.14.

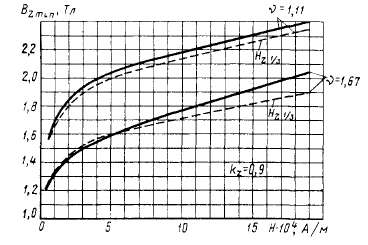
При расчете по индукции в сечении на высоте 7з от основания погрешность метода очень велика (рис. 2.15), и при больших ин-дуциях в зубце, когда необходимо учитывать проводимость паза, рекомендуется производить расчет по трем сечениям.

Магнитное напряжение зубцового слоя влияет на распределение магнитной индукции в воздушном зазоре. Считая известными скалярные магнитные потенциалы поверхности полюса и сердечника якоря, определяем разность между ними, равную переходному магнитному напряжению:

В какой-либо точке воздушного зазора, расположенной на расстоянии х от оси главного полюса,

где 6* — теоретические значения воздушного зазора в данной точке.

Рис. 2.15. Магнитные характеристики зубцового слоя

Уравнение (2.69) решается графически (рис. 2.16). В правом координатном углу показана зависимость между индукцией в воздушном зазоре и магнитным напряжением в зубцах. В левом координатном углу — пучок прямых линий, соответствующих уравнению (2.67), при заданном значении воздушного зазора. Котангенс угла наклона прямой к оси абсцисс

При заданном значении индукции В_в0 магнитное напряжение определяется как отрезок прямой, заключенный между кривой f-_z = f(B₆) и лучом, соответствующим заданному зазору (рис. 2.16).

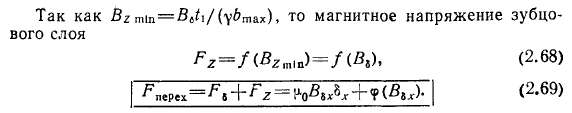
Если задано значение -F_nepex, то можно получить соответствующие значения В₆ в различных точках воздушного зазора.

На рис. 2.17 показано распределение магнитной индукции В₆ в машине с зазором, равномерно увеличивающимся от середины к

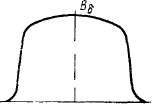Рис. 2.16. Диаграмма для области воздушного зазора — зубцового слоя

Рис. 2.17. Распределение индукции в эксцентрическом воздушном зазоре

краям. При больших значениях тока возбуждения распределение индукции приближается к прямоугольному, как в машине с неизменным воздушным зазором. Это явление хорошо объясняется с помощью семейства переходных характеристик, изображенного на рис. 2.16. При больших значениях fnepex и Bt, происходит насыщение зубцов, и сильное изменение воздушного зазора не приводит к значительному изменению индукции.

Содержание
Предыдущий § Следующий