Содержание  Главная (библиотека)
Предыдущий § Следущий

§ 4.3. МАГНИТОДВИЖУЩИЕ СИЛЫ ОБМОТКИ ПЕРЕМЕННОГО ТОКА

Магнитодвижущая сила однофазной сосредоточенной катушки. На рис. 4.20 одним витком схематично показана сосредоточенная статорная катушка А двухполюсной машины с диаметральным шагом. При прохождении тока по катушке создается магнитный

поток, который так же, как и в трансформаторе, можно условно разбить на два: поток Ф_s рассеяния и поток Ф взаимоиндукции. Поток рассеяния не проходит через воздушный зазор, он связан только с витками этой катушки и не сцеплен с другими обмотками и не

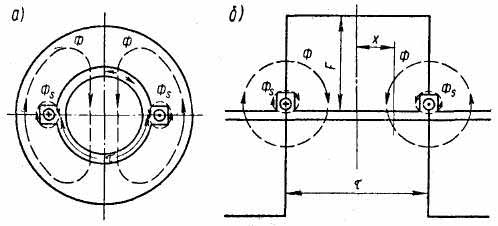Рис. 4.20. Потоки и м. д. с, создаваемые сосредоточенной обмоткой, расположенной на статоре: а — путь магнитного потока; б — развертка вдоль воздушного зазора

оказывает на них влияния. При помощи потока взаимоиндукции передается электромагнитная энергия от статора к ротору.

Поток взаимоиндукции Ф два раза пересекает воздушный зазор. Если пренебречь магнитным сопротивлением участков стали,

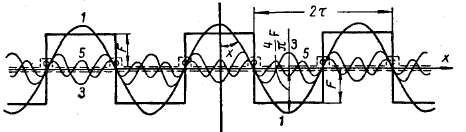Рис. 4.21. Разложение м. д. с. многополюсной машины на основную и высшие гармоники

то создаваемая катушкой м. д. с, необходимая для проведения потока через один воздушный зазор,

где ω_k — число витков катушки;

i — ток катушки.

На рис. 4.20, б сплошной линией показан пространственный прямоугольник распределения м. д. с. в воздушном зазоре по расточке статора.

В многополюсной машине м. д. с. F(x) является периодической функцией х с периодом 2τ (рис. 4.21). Для удобства анализа функцию F(x) распределения м. д. с. можно разложить в гармонический ряд Фурье на основную и высшие пространственные гармоники.

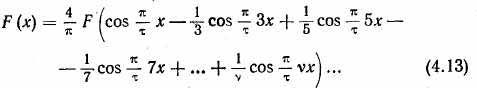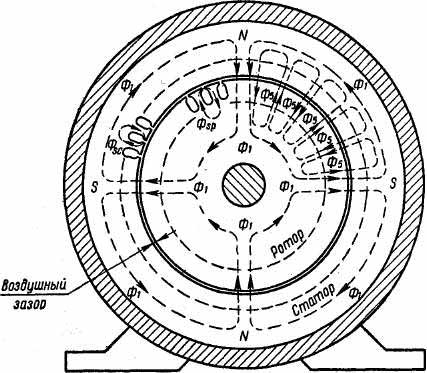
Рис. 4.22. Распределение потоков в четырехполюсной асинхронной машине

На рис. 4.21 показаны основная 1, третья 3 и пятая 5 гармоники. На рис. 4.22 стрелками показаны пути потока первой гармоники Ф₁ и пятой пространственной гармоники Ф₅, а также пути потоков пазового рассеяния статора Ф_s.c и ротора Ф_s.р машины, имеющей четыре полюса (2р = 4).

При дальнейшем рассмотрении высшие пространственные гармоники учитываться не будут. Тогда выражение распределения м. д. с. в воздушном зазоре примет вид

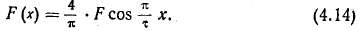
Оси фаз трехфазной обмотки сдвинуты относительно друг друга на треть пространственного периода основной гармоники, что соответствует 120 эл. град. Если принять, что ось фазы А совпадает с началом координат, то м. д. с. фаз трехфазной обмотки имеют следующее выражение:

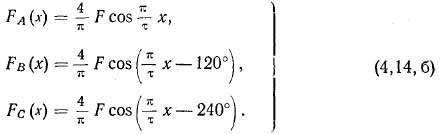Примем, что переменный ток, проходящий по катушке фазы А, изменяется по закону синуса

Подставляя (4.15) в (4.12) и (4.14), получаем выражение м. д. с, возникающей при прохождении по катушке фазы А переменного тока

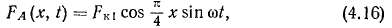где

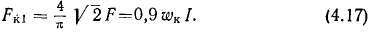Из (4.16) следует, что все точки косинусоидально распределенной в пространстве м. д. с. пульсируют во времени по закону синуса. При этом распределение м. д. с. в воздушном зазоре всегда со-

катушек, каждая из которых укладывается в отдельных пазах. На рис. 4.24 представлены м. д. с. обмотки при q = 3. Для м. д. с. каждой катушки выделена основная гармоника, которая сдвинута в пространстве от соседней на электрический угол α, определяемый сдвигом между пазами. Для определения основной волны м. д. с. обмотки, основные волны отдельных катушек надо геометрически сложить (рис. 4.24). Амплитуда м. д. с. однофазной обмотки

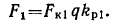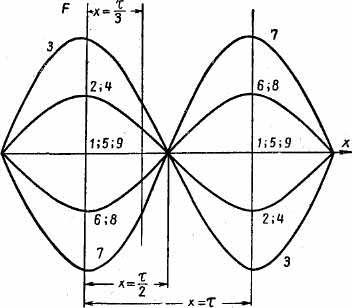Рис. 4.23. Изменение пульсирующей волны м. д. с. во времени

В многополюсной обмотке q катушек располагаются под каждой парой полюсов. Число витков многополюсной обмотки ω = ω_kpq. С учетом укорочения шага и скоса пазов амплитуда м. д. с. (4.17) многополюсной обмотки равна

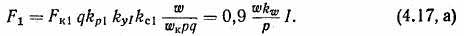Магнитодвижущая сила однофазной распределенной и укороченной обмотки с учетом (4.17, а) может быть выражена формулой

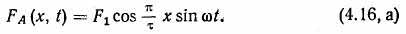Магнитодвижущая сила двухфазной обмотки. На рис. 4.25 двумя витками А и В представлена двухфазная обмотка, питаемая токами, сдвинутыми по фазе на четверть периода. Если пред-

положить, что ток в фазе А изменяется согласно выражению (4.15), то ток в фазе В

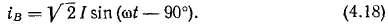Магнитодвижущая сила фазы В с учетом (4.14, а), (4.18) и (4.17, а) выражается

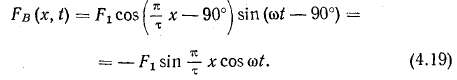Магнитодвижущая сила фазы А, как и раньше, определяется формулой (4.16, а).

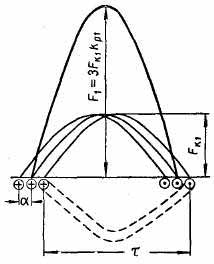Рис. 4.24. Сложение основных волн м. д. с. распределенной обмотки

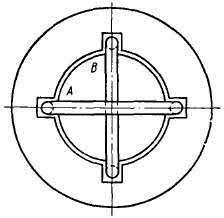Рис. 4.25. Расположение витков фаз А и В двухфазной обмотки двухполюсной машины

Для определения результирующей м. д. с. двухфазной обмотки надо сложить F_a(x, t) и F_b(х, t):

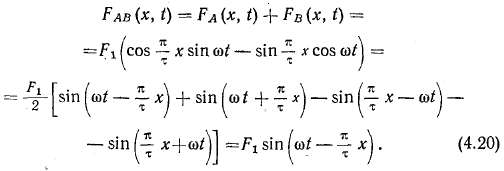Из (4.20) следует, что м. д. с. F_Ab(x, t) двухфазной обмотки представляет собой вращающуюся круговую волну, амплитуда которой сохраняет свою величину неизменной. Амплитуда вра-

щающейся волны двухфазной обмотки равна амплитуде пульсирующей м. д. с. одной фазы.

Убедимся в том, что формула (4.20) действительно представляет собой математическую запись вращающейся волны. Для этого проанализируем выражение при нескольких значениях времени. Согласно (4.20) точка с пространственной координатой х, в которой м. д. с. F_ab(х, t) имеет максимальную амплитуду, с течением времени перемещается вдоль расточки статора. Действительно,

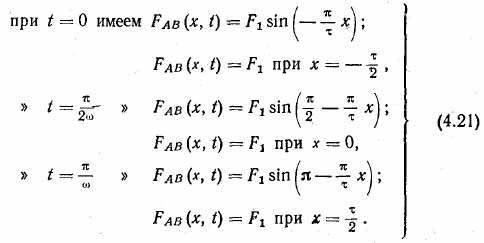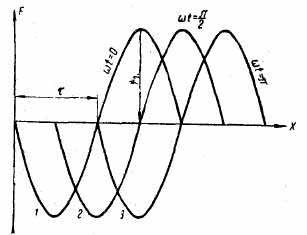
Рис. 4.26. Изменение вращающейся волны м. д. с. во времени

На рис. 4.26 представлено положение одного пространственного периода волны м. д. с. для моментов времени, указанных в выражениях (4.21). При перемещении точки кривой, имеющей текущую координату х, волна м. д. с. сохраняет свое амплитудное значение F₁. В этом случае

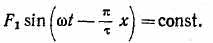Отсюда следует, что всегда

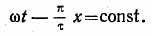Продифференцировав это выражение по времени, имеем

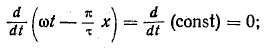
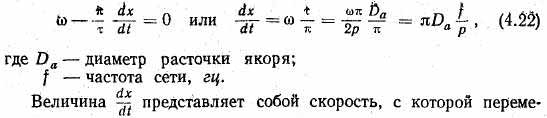щается амплитуда волны F₁. Из (4.22) видно, что при заданном диаметре расточки статора скорость вращения волны м. д. с. пропорциональна частоте сети и обратно пропорциональна числу полюсов машины.

Заметим, что волна, описанная формулой (4.20) (рис. 4.26), вращается вправо. Если бы в формуле (4.20) стоял знак «плюс», то волна вращалась бы влево. Понятие левого и правого вращения условное, оно зависит от принятого направления координатных осей.

Рассмотрим преобразование (4.20) с физической точки зрения. При сложении каждая из пульсирующих волн м. д. с. обмоток фаз А и В разлагается на две волны, вращающиеся в противоположные стороны (правовращающуюся и левовращающуюся). Их амплитуды равны половине амплитуды пульсирующей волны. Правовращаю-щиеся волны двух, фаз обмотки совпадают по фазе, они складываются и образуют одну вращающуюся волну, амплитуда которой равна амплитуде пульсирующей. Левовращающиеся волны оказываются направленными встречно (т. е. они вращаются в одну сторону со сдвигом по фазе на 180°) и компенсируют друг друга.

Магнитодвижущая сила трехфазной обмотки. Токи трехфазной системы определяются выражениями

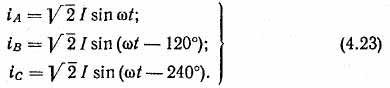С учетом (4.14,б), (4.23) и (4.17, а) м. д. с. фаз трехфазной обмотки равны:

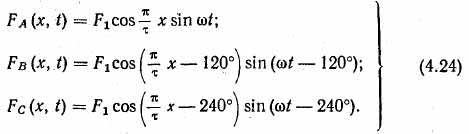Для определения результирующей м. д. с. трехфазной обмотки сложим м. д. с. отдельных фаз. С этой целью разложим пульсирующую волну м. д. с. каждой фазы на две, вращающиеся в противо-

положные стороны, амплитуды Которых равны пбловйне Пульсирующей. Все правовращающиеся волны совпадают по фазе, поэтому они складываются и образуют одну вращающуюся волну м. д. с, амплитуда которой в полтора раза больше амплитуды пульсирующей волны. Левовращающиеся волны компенсируют друг друга, поскольку они сдвинуты в пространстве на 120°:

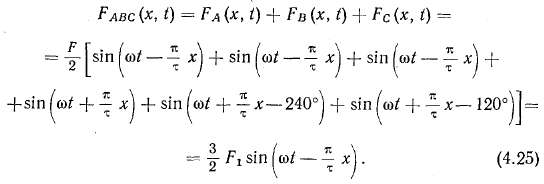Анализируя (4.25), видим, что при прохождении по трехфазной обмотке симметричных токов создается вращающаяся круговая волна м. д. с., амплитуда которой в 3/2 раза больше амплитуды пульсирующей волны одной фазы обмотки.

Пространственная векторная диаграмма м. д. с. Вектор м. д. с. пространственной диаграммы определяет величину и направление основной пространственной гармоники м. д. с. для данного момента времени. Углы, определяющие направление векторов, выражаются в электрических

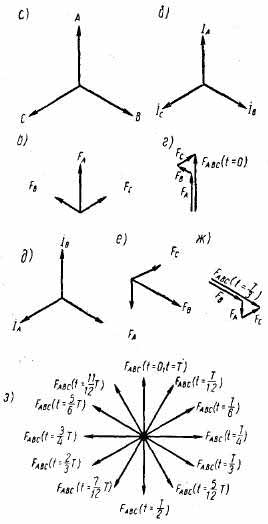Рис. 4.27. Построение пространственных векторов м. д. с. трехфазной обмотки: а — пространственное направление осей фаз обмоток; б —векторная диаграмма токов при t = 0; в — м. д. с. фаз обмоти при t = 0; г — результирующая м. д. с. обмотки при t = 0; д — векторная диаграмма токов при t =T/3; е — м. д. с. фаз обмотки при t =T/3; ж — результирующая м. д. с. обмотки при t = T/3; з — результирующая м. д. с. обмотки в различные моменты времени

градусах. Таким образом, угол, соответствующий двум полюсным делениям, на пространственной диаграмме равен 360°.

На рис. 4.27, а показано пространственное расположение осей фаз трехфазной обмотки. Вектор пульсирующей м. д. с. фазы направлен по ее оси. Если ток в данный момент времени имеет положительное значение, то вектор м. д. с. совпадает с направлением оси фазы; если ток имеет отрицательное значение, то вектор м. д. с. направлен встречно. С учетом масштаба длина вектора м. д. с. фазы может быть рассчитана по выражению (4.17, а).

Чтобы определить вектор м. д. с. трехфазной обмотки, необходимо построить для данного момента времени векторы м. д. с. отдельных фаз и сложить их. Для этого следует предварительно вычертить временную векторную диаграмму токов. На рис. 4.27, б представлена диаграмма токов для момента времени t = 0. Когда ток в фазе достигает положительного максимального значения вектор тока J_a направлен вертикально вверх. На диаграмме видно, что токи в фазах i_B и i_C направлены встречно по отношению к току фазы A ив два раза меньше его, т. е.

Построение графика пространственного распределения м. д. с. Для любого момента времени можно построить кривую распределения м. д. с. F(x) вдоль расточки статора. Для этого необходимо

предварительно составить для каждой фазы таблицу схемы обмотки (например, рис. 4.17, б). Затем полезно вычертить схему обмотки (часто бывает достаточно вычертить только одну фазу, см. рис. 4.17, в).

После составления таблицы схемы обмотки можно приступить к построению графика мгновенного распределения м. д. с. Для этого сначала вычерчивают диаграмму фазных токов в заданный момент

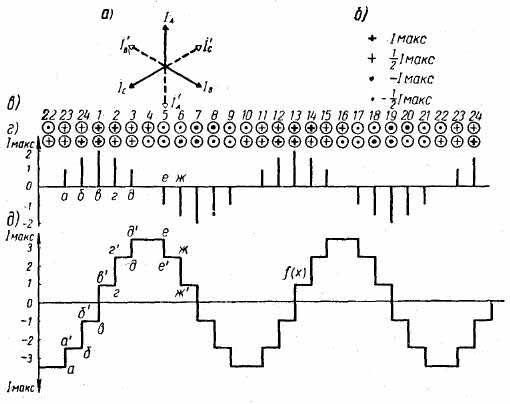Рис. 4.28. Графическое построение м. д. с. трехфазной обмотки для момента -времени, когда ток А имеет максимальное значение: а — векторная диаграмма фазных токов; б — условные обозначения величины и направлений тока в секции; в — значение и направление токов в верхних и нижних секциях; г — график распределения объема тока в пазу вдоль расточки статора; д — распределение м. д. с. обмотки

времени, например, когда ток в фазе А достигает максимального положительного значения (рис. 4.28, а). Для двухслойной обмотки удобно на векторной диаграмме токов изображать положительные I'_A, I'_B, I'_C и отрицательные I'_A, I'_B, I'_C направления. Токи в фазах обмотки для этого момента времени соответствуют выражению (4.26). Далее условно обозначают кружками верхние и нижние стороны секций (рис. 4.28, в) и над соответствующими кружками ставят номер паза, в котором заложены секции. Пользуясь таблицей обмотки (рис. 4.17, б), отмечают в кружках направление тока («+» или «·») данной секции.

Чтобы различать на диаграмме величину токов, их обозначения на рис. 4.28, б выполнены разной толщиной. Сначала отмечают направление токов в секциях, принадлежащих фазе А обмотки. В верхнем кружке (рис. 4,28, в), обозначающем начальную секцию этой фазы (кружок 1), поставлен крестик. В следующем кружке этой фазы поставлена точка. При обходе любой фазы от данной секции к последующей крестики и точки чередуются. В данный момент времени токи в фазах В и С имеют отрицательное значение. Поэтому в кружках, обозначающих начальные секции этих фаз (5 и 9), поставлены точки. Далее построение ведется аналогично (рис. 4.28, в).

Зная распределение тока обмотки (рис. 4.28, в), можно определить объем тока в каждом пазу. Для этого надо просуммировать (с учетом направления) токи в верхнем и нижнем слоях, а затем следует построить график распределения объема тока в пазу вдоль расточки статора. С достаточной для практических построений точностью можно считать, что весь объем тока в пазу сосредоточен в середине паза. Для построения этого графика под каждой парой кружков одного паза откладывают ординату, соответствующую значению объема тока с учетом знака. Далее находят пазы, под которыми м. д. с. F(x) проходит через нуль, и пазы, под которыми F(x) достигает максимального значения. При этом следует иметь в виду, что кривая распределения м. д. с. в воздушном зазоре F(x) является интегральной по отношению к графику объема тока в пазу. Поэтому под пазом, в котором объем тока имеет максимальное значение, кривая распределения м. д. с. F(x) проходит через нуль (пазы 1, 7, 13 и 19). Если имеется несколько расположенных рядом пазов, в которых объем тока имеет максимальное значение, то кривая м. д. с. проходит через нуль по середине между ними.

Максимальное значение кривой м. д. с. F(x) имеет место под теми пазами, в которых объем тока равен нулю (4, 10, 16 и 22). Если при этом ординаты объема тока меняют положительное значение на отрицательное (например, под пазом 4), то здесь максимальное значение м. д. с. положительное; если ординаты объема тока меняют отрицательное значение на положительное (например, под пазом 22), то здесь максимальное значение м. д. с. отрицательное.

Для построения графика м. д. с. полезно определить амплитуду волны F(x), она равна полусумме расположенных рядом ординат объема тока в пазу, имеющих один знак (или одно направление), например ординаты а, б, в, г, д на рис. 4.28, г.

Построение кривой распределения м. д. с. удобно начать с паза, в котором она имеет максимальное значение, например максимальное отрицательное значение (паз 22), Под пазом 22 откладывают вниз от оси абсцисс ординату, соответствующую максимальному значению м. д. с. и через ее конец проводят горизонтальную прямую до пересечения с точкой, соответствующей прорези соседнего паза 23, т. е. с точкой а (рис. 4.28, д). В точку а сносят ординату объема

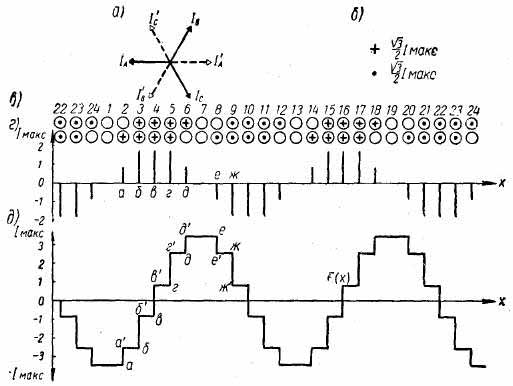
Рис. 4.29. Графическое построение м. д. с. трехфазной обмотки для момента времени, когда ток в фазе А равен нулю:

а — звезда фазных токов; б — условные обозначения величины и направления токов в секциях; в — значение и направление токов в верхних и нижних секциях; г — график распределения объема тока в пазу вдоль расточки статора; д — распределение м. д. с. обмотки

откладывают вниз. Продолжая построение дальше, получают полный график распределения м. д. с. F(x) для данного момента времени (рис. 4.28, д).

На рис. 4.29 показано построение графика распределения м. д. с. F(x) для момента времени, когда ток в фазе А равен нулю, т. е. через четверть периода. Построение этого графика аналогично описанному выше, обозначения приняты те же. Сравнивая рис. 4.28, д и 4.29. д, видим, что за время, соответствующее четверти периода изменения тока в обмотке, максимальное значение м. д. с. F(x), оставаясь тем же по величине, сместилось вдоль расточки статора на четыре паза, что соответствует четверти пространственного перио-

да. Кривая м. д. с. несколько изменила форму. Если продолжить построение для других моментов времени, то будет видно, что за полный период изменения тока м. д. с. обмотки перемещается вдоль расточки статора на расстояние, соответствующее пространственному периоду.

М. д. с., которая за время периода изменения тока перемещается с равномерной скоростью на один пространственный период, называют синхронно вращающейся.

Изменение направления вращения м. д. с. Для изменения направления вращения м. д. с. трехфазной обмотки достаточно переключить две какие-либо фазы, присоединенные к сети. Действительно, если переключить фазы В и С, то в фазе обмотки В будет проходить ток i_C, в фазе С — ток i_B. Складывая м. д. с. отдельных фаз с учетом (4.14, б) и (4.23), получаем выражение вращающейся м. д. с. обмотки

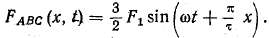В формуле появился знак плюс, поэтому м. д. с. вращается влево, т. е. она изменила направление вращения на обратное.

Магнитодвижущая сила двухфазной обмотки при изменении тока в одной из фаз. В системах автоматики применяются двигатели, статор которых имеет две обмотки, сдвинутые в пространстве на 90 эл. град. Форму м. д. с. таких двигателей можно регулировать изменением тока по величине или фазе в одной из обмоток.

В случае, если амплитуды пульсирующих фазных м. д. с. не равны, например если F_1B<F_1A, то, делая преобразования, аналогичные (4.20), имеем

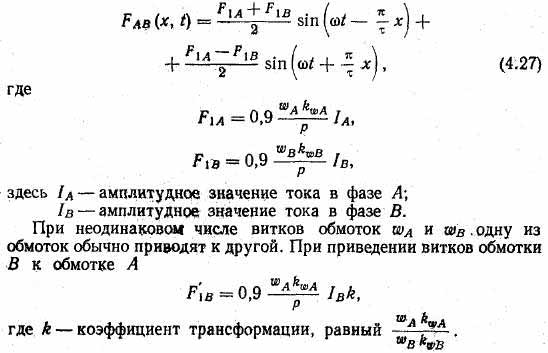
Из (4.27) следует, что при неравенстве амплитуд F_1a и F_1B м. д. с. двухфазной обмотки состоит из двух волн, которые вращаются в противоположные стороны с угловой частотой ω. Аналогично тому, как показано на рис. 4.27, з, в каждый момент времени вращающиеся волны могут быть представлены векторами, длины которых соответственно равны

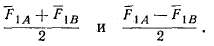
Общий случай вращающейся эллиптической м. д. с. Эллиптичность вращающейся м. д. с. может быть вызвана неравенством амплитуд фазных м. д. с, несимметричным сдвигом токов по фазам или несимметричным расположением осей фаз т фазной обмотки. В любом из этих случаев при анализе м. д. с. удобно систему фазных м. д. с. разложить на прямую, обратную и нулевую последователь-

ности. Если все обмотки имеют одинаковое число витков и расположены симметрично, то можно не раскладывать м. д. с, а ограничиться разложением системы токов на токи прямой (I₁), обратной (I₂) и

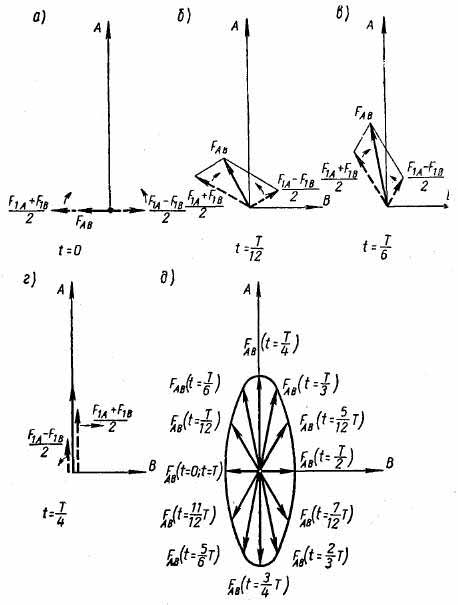Рис. 4.30. Построение пространственных векторов м. д. с. двухфазной обмотки для случая F_1A>F_1B

нулевой (I₀) последовательности. Система токов нулевой последовательности не создает никаких вращающихся м. д. с, система токов прямой последовательности создает синхронно вращающуюся м. д. с, которая может быть правовращающейся,

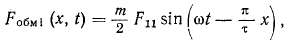
где амплитудам, д. с. однофазной обмотки, содаваемая током прямой последовательности,

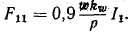Система токов обратной последовательности создает м. д. с., которая вращается с той же скоростью в противоположную сторону и может быть выражена формулой

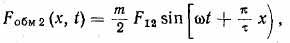где амплитуда м. д. с. однофазной обмотки, создаваемая током обратной последовательности,

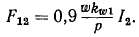Таким образом, при несимметрии токов имеют место две вращающиеся в противоположные стороны м. д. с, пропорциональные токам прямой и обратной последовательности. Их действие эквивалентно вращающейся эллиптической м. д. с, амплитуда которой

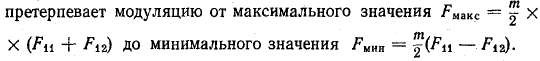Высшие пространственные гармоники м. д. с. Анализируя формулу (4.13), видим, что, помимо основной пространственной гармоники, м. д. с. сосредоточенной катушки имеет также спектр высших пространственных гармоник. Магнитодвижущая сила синусной обмотки может приближаться к синусоидальному распределению, однако в действительности м. д. с. обмотки и в этом случае имеет высшие пространственные гармоники. При симметричном питании трехфазной обмотки м. д. с. высших пространственных гармоник (в частности третьей и ей кратных) не оказывают существенного влияния на работу машины. При питании двухфазной обмотки, в особенности в случае эллиптичности вращающегося поля основной гармоники, высшие гармонические м. д. с. (в частности третья) могут оказать существенное влияние на работу электрической машины. При прохождении синусоидального переменного тока (4.15) по однофазной обмотке м. д. с. υ-ой пространственной гармоники с учетом (4.13) имеет следующее выражение:

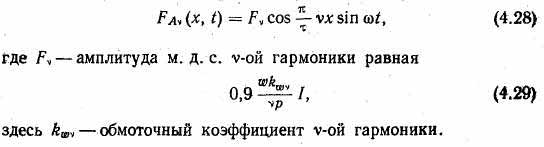
Магнитодвижущая сила υ-ой пространственной гармоники, согласно (4.28), представляет собой косинусоиду, пространственный период которой меньвде основного соответственно порядку гармони-ни, т. е. в υ раз (на рис. 4.21 показано распределение высших пространственных гармоник, порядок которых равен трем и пяти, на рис. 4.22 показаны пути потоков Ф₅ пятой пространственной гармоники). Все точки υ-ой пространственной гармоники однофазной м. д. с, согласно формуле (4.28), сохраняя в пространстве косинусоидальное расположение, изменяются во времени с частотой тока по закону синуса. Магнитодвижущая сила υ-ой гармоники фазы В двухфазной обмотки с учетом (4.18) равна

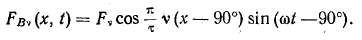Разлагая пульсирующую м. д. с. фаз А и В двухфазной обмотки на две волны, вращающиеся в противоположные стороны, и складывая отдельно левобегущие и отдельно правобегущие волны, получаем выражение для

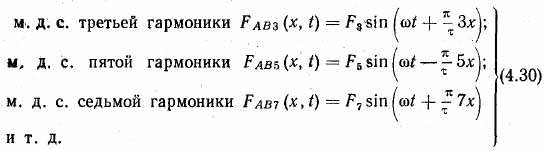Из равенств (4.30) видим, что каждая м. д. с. высшей нечетной гармоники следующего порядка вращается встречно по отношению к предыдущей.

Аналогичным путем может быть выведено выражение м. д. с. высшей (υ) пространственной гармоники трехфазной обмотки

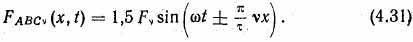Анализируя выражение (4,31), видим, что амплитуда вращающейся м. д. с. υ-ой гармоники трехфазной обмотки в полтора раза больше, чем амплитуда пульсирующей υ-ой гармоники одной фазы.

Следует обратить внимание на то, что м. д. с. трехфазной обмотки третьей и кратных ей гармоник равна нулю, так как при разложении пульсирующих волн фазных м. д. с. сумма левовращающихся волн равна нулю. Сумма правовращающихся также равна нулю. Таким образом, порядок гармоник м. д. с. которые в трехфазной обмотке создают вращающиеся поля, может быть представлен выражением

υ = 3n± 1,

где п = 1,2, 3, 4, ...

Обычно кривая распределения м. д. с. является симметричной. В этом случае отсутствуют четные гармоники и порядок гармоник соответствует формуле

υ = 6n± 1, (4.32)

где п = 1, 2, 3 ...

Гармоники (5, 11, 17 и т. д.), порядок которых может быть выражен числом υ = 6п—1, создают обратно вращающиеся поля по отношению к полю первой гармоники. В выражении м. д. с. таких гармоник (4.31) должен стоять знак «плюс». Гармоники (7, 13, 19 и т. д.), порядок которых может быть выражен числом υ = 6п+1 создают прямо вращающиеся поля. В выражении м. д. с. (4.31) в этом случае должен стоять знак «минус». Сравнивая (4.30) и (4.32) видим, что υ-ые гармоники двухфазной и трехфазной обмоток вращаются в противоположные стороны. Например, м. д. с. пятой гармоники двухфазной обмотки вращается согласно, а трехфазной встречно по отношению к направлению вращения м. д. с. первой гармоники.

Из выражений (4.30) и (4.31) следует, что в любой момент времени амплитуда вращающейся волны сохраняет свое значение, но перемещается в пространстве. Поэтому

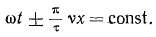Продифференцировав это выражение по времени, имеем

Сравнивая (4.33) и (4.22), видим, что поля высших пространственных гармоник вращаются в υ раз медленнее, чем синхронное поле, создаваемое основной гармоникой.

Вращающиеся поля высших пространственных гармоник создают вредные паразитные моменты и добавочные потери.

Высшие временные гармоники м. д. с. При однофазном питании и других схемах обмоток, в которых могут проходить токи нулевой последовательности, в случае насыщения стали магнитопровода возникают третья и кратные ей временные гармоники тока. Выпрямление переменного тока для нужд электротяги и инвертирование постоянного тока при передаче электроэнергии может также привести к появлению в кривой напряжения и тока сети высших временных гармоник. В последнем случае ток обмотки состоит из суммы основной и высших временных гармоник:

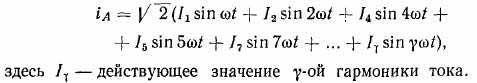
Гармоники тока, кратные трем, часто отсутствуют. При некоторых схемах коммутации четные гармоники тока также отсутствуют.

Проходя по обмотке, каждая γ-ая гармоника тока создаст свою м. д. с. Обычно пренебрегают высшими пространственными гармониками м. д. с, так как их влияние по сравнению с основной гармоникой невелико. Тогда γ-ая временная гармоника тока, проходя по однофазной обмотке А, создаст пульсирующую м. д. с.

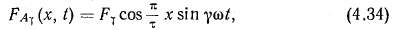где амплитуда м. д. с. γ-ой временной гармоники

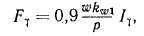Анализируя (4.34), видим, что основная гармоника м. д. с, создаваемая γ-ой временной гармоникой тока, пульсирует во времени в γ раз чаще, чем волна м. д. с, создаваемая основной гармоникой тока.

Третьи гармоники тока, имеющие одинаковые амплитуды, проходя по фазам А и В двухфазной обмотки, создают вращающуюся м. д. с.

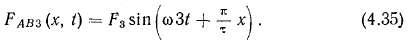В трехфазной обмотке третьи гармоники тока не создают вращающихся полей. При прохождении гармоник тока, некратных 3, создается вращающаяся м. д. с.

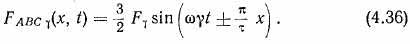Анализируя выражения (4.35) и (4.36), видим, что амплитуда волны м. д. с. перемещается вдоль воздушного зазора, сохраняя в любой момент времени свою величину. При этом

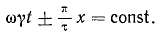Продифференцировав это выражение по времени, имеем

Сравнивая (4.37) и (4.22), видим, что м. д. с, создаваемая γ-ой гармоникой тока, вращается в γ раз быстрее, чем основная, вращающаяся синхронно. Направление вращения м. д. с. γ-ой гармоники трехфазной обмотки определяется согласно выражению (4.32), в котором в этом случае букву v следует заменить на γ.

Вращающиеся поля временных гармоник высшего порядка являются вредными, так как они создают паразитные асинхронные моменты и добавочные потери в обмотках.

ВОПРОСЫ

1.   Каковы условия создания вращающейся, круговой м. д. с_;? В чем состоит различие между вращающимися эллиптической и круговой м. д. с ? Чем отличается скорость вращения круговой м. д. с. от эллиптической? В каких случаях многофазная обмотка создает пульсирующую м. д. с?

2.   Как можно изменить скорость вращения м. д. с. многофазной обмотки? Как зависит скорость вращения м. д. с. обмотки от числа полюсов?

3.  В чем состоит различие между высшими временными и пространственными гармониками м. д. с? В результате чего имеют место высшие пространственные гармоники? В каком случае они отсутствуют? При каких условиях появляются высшие временные гармоники м. д.с.? В каком случае они отсутствуют? Как распределяется в воздушном зазоре пространственная гармоника высшего порядка, создаваемая синусоидальным током? Чему равно ее полюсное деление? Как распределяется в воздушном зазоре волна временной гармоники высшего порядка? Чему равно ее полюсное деление?

4.  С какой частотой пульсируют пространственная и временная гармоники высшего порядка м. д. с. однофазной обмотки? С какой скоростью вращается вдоль воздушного зазора волна временной и пространственной гармоник высшего порядка трех-или двухфазной обмотки? Почему м. д. с. третьей пространственной и временной гармоник отсутствуют в трехфазной обмотке, но имеют место в двух- и однофазной обмотках?

Содержание  Главная (библиотека)
Предыдущий § Следущий