Содержание
< назад вперед >
§ 67. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ
АКТИВНОГО СОПРОТИВЛЕНИЯ И ИНДУКТИВНОСТИ (r, L)
На схемах цепей переменного
тока сопротивления обозначаются, как показано на рис. 145. На практике часто
встречаются участки электрической цепи, обладающие как активным, так и
индуктивным и емкостным сопротивлениями.
Пусть необходимо определить
напряжение сети, которое нужно приложить к зажимам катушки, чтобы по ней мог
проходить переменный ток. Катушка имеет активное и индуктивное сопротивления.
Поэтому напряжение сети должно уравновесить активное падение напряжения, а
также э. д. с. самоиндукции, возникающую в катушке.
Построим векторную диаграмму
и графики для этого случая.
На рис. 146 вектор I обозначает переменный ток катушки. Э. д. с.
самоиндукции EL в катушке отстает по фазе
от тока на 90°.
Часть напряжения сети,
уравновешивающая э. д. с. самоиндукции, показана вектором UL, который равен и противоположен вектору EL.
Часть напряжения сети, равная падению напряжения в активном сопротивлении,
изображена вектором Ua, совпадающим по фазе с током. Напряжение сети должно
быть равно геометрической сумме падений напряжения: активного Ua и
индуктивного UL. Геометрическая сумма берется потому, что Ua и UL
на рис. 146 изображаются векторами, а векторы складываются геометрически.
Оба эти напряжения
расположены под углом одно к другому. Поэтому для получения их геометрической
суммы необходимо на векторах Ua и UL
построить параллелограмм. Его диагональ (равнодействующая) представляет собой вектор напряжения сети U.
Как видно из рис. 146, вектор
тока / отстает от вектора напряжения U на угол φ:
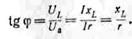
В катушке, содержащей только
индуктивное сопротивление, ток отставал от напряжения сети на угол 90°, а при
учете активного сопротивления ток отстает от напряжения сети на угол, меньший,
чем 90°. И только когда индуктивность равна нулю, ток в катушке совпадает по фазе
с напряжением сети.
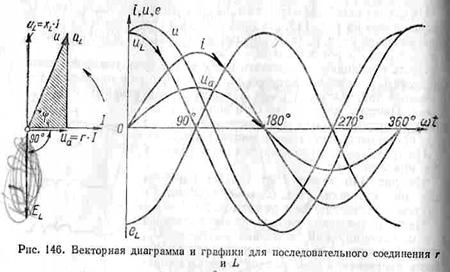
Построим график мгновенной
мощности для последовательного соединения активного сопротивления и
индуктивности (рис. 147).
Из представленного графика
видно, что средняя, или активная, мощность не равна нулю, как было в цепи с
индуктивностью или емкостью. В этом случае в течение некоторой части периода
энергия в цепи расходуется на нагрев сопротивления и образование магнитного
поля катушки (мощность положительна). В течение другой части периода энергия
возвращается в сеть (мощность отрицательна).
Таким образом, средняя, или
активная, мощность Р переменного тока зависит не только от величин напряжения
U и тока I, но также и от сдвига фаз φ
между ними.
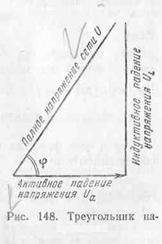
Заштрихованный на рис. 146
треугольник напряжений начертим отдельно (рис. 148). Так как этот треугольник
прямоугольный, то в случае, когда одна сторона неизвестна, ее можно определить
с помощью теоремы Пифагора (квадрат гипотенузы равен сумме квадратов катетов).
Следовательно,
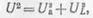
откуда
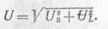
Пример 7. Определить напряжение сети, которое необходимо
приложить к зажимам катушки, чтобы в ней протекал ток в 5 а, если активное
сопротивление катушки г равно 6 ом, а индуктивное сопротивление хL, равно 8 ом.
Активное падение напряжения

Индуктивное падение напряжения

Полное падение напряжения
равно напряжению сети:
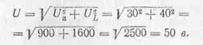
Необходимо отметить, что показание вольтметра сети не равно
арифметической сумме значение 
Если стороны
треугольника напряжений (рис. 149, а)
разделить на величину тока / (рис. 149, б), то углы треугольника от этого не
изменятся, и мы получим новый треугольник, подобный первому,— треугольник
сопротивлений (рис. 149, е).
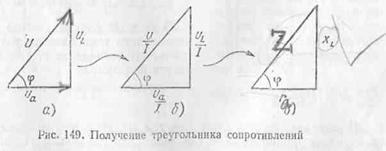
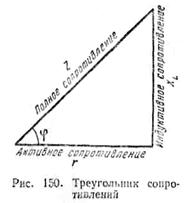
В треугольнике сопротивления,
показанном отдельно на рис. 150, все стороны обозначают сопротивления, причем
гипотенуза его является полным сопротивлением цепи.
Из треугольника сопротивлений
видно, что полное сопротивление z равно
геометрической сумме активного r к индуктивного
хL сопротивлений.
Применяя теорему Пифагора к
треугольнику сопротивления, получаем
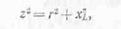
откуда
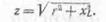
Из треугольника сопротивлений
также получаем:
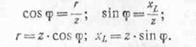
Если
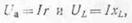
То
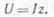
Из формулы 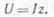 видно, что видно, что
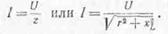
Пример 8.
Определить ток, проходящий через катушку, индуктивное сопротивление которой
равно 5 ом, а активное сопротивление равно 1 ом, если напряжение сети
переменного тока равно 12 в.
Определим
полное сопротивление катушки:
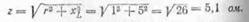
Применяя формулу закона Ома для цепи r, L, получим
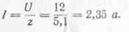
В частных случаях, когда в
цепи переменного тока имеется только активное сопротивление r, ток определяется по формуле
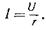
В случаях, если в цепи
имеется индуктивное сопротивление, а активное сопротивление так мало, что им
можно пренебречь, формула закона Ома приобретает вид
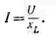
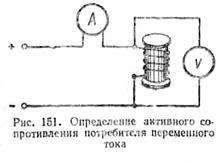
Если необходимо узнать
активное сопротивление потребителя переменного тока (обмотка электродвигателя,
индуктивной катушки или электромагнита),
то нужно включить этот потребитель в
цепь постоянного тока (рис.
151). Деля показание вольтметра, включенного к зажимам потребителя, на
показание амперметра, включенного последовательно в цепь, получим величину
активного сопротивления,
так как
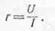
Сказанное справедливо только
при низких частотах, когда явлением
поверхностного эффекта можно пренебречь и считать активное сопротивление
потребителя равным его сопротивлению при постоянном токе.
| 
