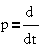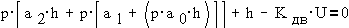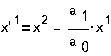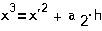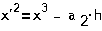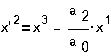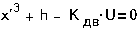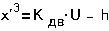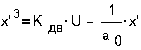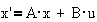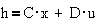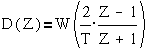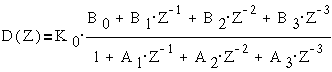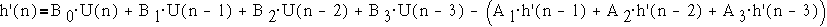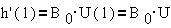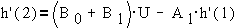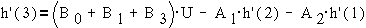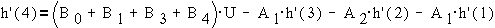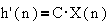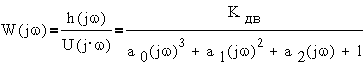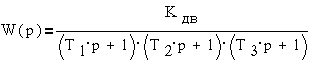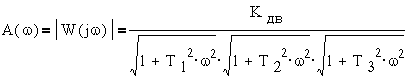- 1.1. Уравнения
движения. Электромеханические аналогии.
- 1.2.
Электромеханические аналогии. Уравнения Лагранжа- Максвелла.
- 1.3. Энергия
электрического и магнитного полей. Силы и моменты, возникающие при
электромеханическом преобразовании энергии.
- 1.4. Электромагнитные,
электродинамические и электростатические преобразователи.
- 1.5. Классификация
электромеханических преобразователей.
- 1.6. Представление
электромеханических преобразователей как преобразователей сигналов
(информации).
- 1.7. Анализ
простейшего электромеханического преобразователя.
- 1.8. Упражнения и контрольные
вопросы к главе 1.
1.1. Уравнения движения.
Электромеханические аналогии
Механическая
система обладает энергией. Суммарная энергия механической системы состоит из
трех составляющих:
- кинетической энергии
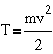 для
поступательного движения и
для
поступательного движения и 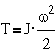 для вращательного
движения;
для вращательного
движения;
- потенциальной энергией П;
- мощностью рассеяния (диссипации) D.
Кинетическая
энергия - энергия движения системы, потенциальная - энергия, запасаемая
упругими элементами, в частности, пружинами. Если пружина работает не
растяжение (сжатие), то 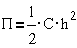 , где C- жесткость, а h-
перемещение. Если пружина работает на скручивание, то
, где C- жесткость, а h-
перемещение. Если пружина работает на скручивание, то 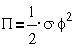 , где s- жесткость, а f- угол поворота.
, где s- жесткость, а f- угол поворота.
Мощность рассеяния
- это обычно энергия, затрачиваемая на преодоление вязкого трения и 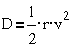 или
или
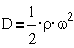 в зависимости от формы движения.
в зависимости от формы движения.
При движении
системы в ней возникают силы, вызванные изменением энергии системы при
изменении ее обобщенных координат h- перемещений или углов
поворота ее элементов.
Механическая
система, имеющая S степеней свободы, описывается уравнениями Лагранжа второго рода:
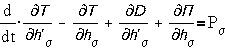 ,
, 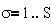 .
.
Здесь :
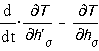 - Даламберовы силы
инерции,
- Даламберовы силы
инерции, 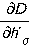 -силы трения,
-силы трения, 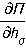 - силы упругого
противодействия,
- силы упругого
противодействия, - Ps- обобщенные внешние
силы (моменты).
Например, для
простейшей системы, имеющей одну степень свободы и совершающей вращательное
движение, имеем
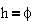 ;
; 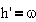 ;
; 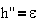
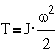 ;
; 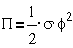 ;
; 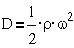 ;
; 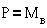
Получим одно
уравнение
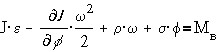 .
.
Если момент инерции
J не зависит от угла поворота f, как это часто бывает, то 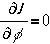 и
уравнение принимает вид:
и
уравнение принимает вид:
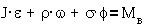 .
.
1.2. Электромеханические
аналогии уравнения Лагранжа-Максвелла
Электромеханическая
система обладает не только механической, но и электрической (электромагнитной)
энергией, сосредоточенной в элементах ее электрической цепи (индуктивностях,
конденсаторах и резисторах).
Поскольку процессы
в электрических цепях описываются также дифференциальными уравнениями,
существуют определенные аналогии между механическими и электрическими
величинами, описывающими поведение системы (см. таблицу).
|
Механическая система
|
Электрическая система
|
|
Первая система аналогий
|
Вторая система аналогий
|
|
Перемещение 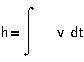
|
Заряд 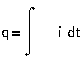
|
Потокосцепление 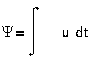
|
|
Скорость V=h`
|
Ток I=q`
|
Напряжение U=Ψ`
|
|
Сила P
|
ЭДС e
|
Ток i
|
|
Масса m
|
Индуктивность L
|
Емкость C
|
|
Механическое сопротивление r
|
Сопротивление R
|
Проводимость G
|
Жесткость C
|
Инверсная емкость
S=c-1
|
Инверсная индуктивность Г
|
|
Кинетическая энергия 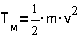
|
Энергия магнитного поля 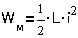
|
Энергия электрического поля 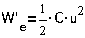
|
|
Потенциальная энергия 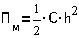
|
Энергия электрического поля 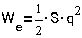
|
Энергия магнитного поля 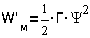
|
|
Мощность рассеяния 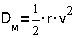
|
Мощность рассеяния 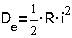
|
Мощность рассеяния 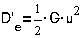
|
Первая система
аналогий между механическими и электрическими цепями более "физична",
поэтому в основном 6удем пользоваться ею, хотя в некоторых случаях применение второй
системы дает более простые уравнения.
Из этой системы
видно, что ЭДС в электрической цепи аналогична силе, индуктивность аналогична
массе и обладает инерционностью, и энергия, запасаемая в магнитном поле,
является кинетической энергией. Конденсатор, аналогично пружине, запасает
энергию, которую логично считать потенциальной. Активное сопротивление
действует аналогично механическому вязкому сопротивлению, и энергия, выделяемая
на нем, рассеивается в виде тепла.
Тогда простейшей
механической цепи, содержащей массу, пружину и вязкое сопротивление, и
описываемой уравнением вида
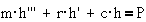
можно поставить в соответствие
простейшую электрическую цепь с последовательно включенными индуктивностью,
емкостью и сопротивлением, описываемую уравнением
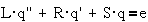
где L·q``- ЭДС
самоиндукции, R·q`- падение напряжения на
сопротивлении, S·q- напряжение на емкости.
В электротехнике
обычно это уравнение записывается в виде:
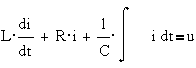
Электромеханическую
систему, имеющую Sm степеней механической
свободы и S1 независимых электрических контуров, учитывая
электромеханические аналогии, можно представить в виде механической системы,
имеющей Sm+S1 степеней свободы и
обладающей
- суммарной электромеханической кинетической
энергией TΣ=TM+WM;
- потенциальной энергией ПΣ=ПМ+WЭ;
- мощностью рассеяния DΣ=DM+DЭ.
Отсюда движение в
такой системе будет описываться уравнениями, аналогичными уравнениям Лагранжа и
называемыми уравнениями Лагранжа-Максвелла :
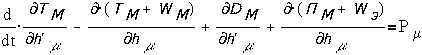 ,
,
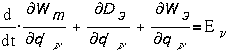
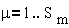
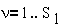
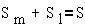
Первые Sm уравнений
описывают механические движения в системе (механические уравнения), последующие
S1
уравнений описывают процессы в электрических цепях (электрические уравнения -
уравнения 2-го закона Кирхгофа).
1.3. Энергия электрического
и магнитного полей. Силы и моменты, возникающие при электромеханическом преобразовании
энергии
В общем виде
энергия электрического поля в объеме V выражается интегралом
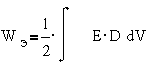 ,
,
где E-
вектор напряженности электрического поля, D- вектор смещения.
Для однородного
поля в конденсаторе
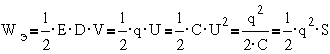
Энергия магнитного
ноля в объеме V также выражается интегралом
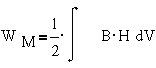
где B-
вектор магнитной индукции, H- вектор напряженности
магнитного поля.
Для однородного
магнитного поля
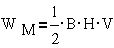
Для n магнитно
связанных контуров с токами получим:
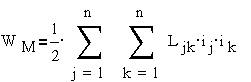 ,
,
где Ljk- индуктивности и взаимные индуктивности контуров
Или 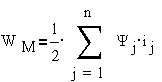 , где Yj- потокосцепление контуров.
, где Yj- потокосцепление контуров.
Тогда для
одиночного контура с током имеем: 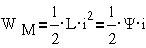
для двух контуров: 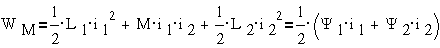 ;
;
для контура с
током, помещенного в магнитный поток Φ: 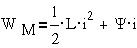 ,
,
где L-
индуктивность контура, Y- потокосцепление внешнего
потока F с контуром.
Рассмотрим
гипотетическую электромеханическую систему. в которой механически связаны
контур с током, помещенный в магнитное поле, и ротор конденсатора, причем при
повороте происходит изменение индуктивности контура, потокосцепления с контуром
и емкости конденсатора.
Общая кинетическая
энергия такой системы будет:
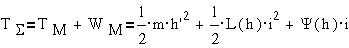 ;
;
потенциальная
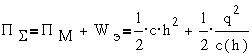 ;
;
рассеяния
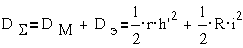
Подставляя это
выражение в уравнение Лагранжа-Максвелла и принимая за обобщенную координату h- угол
поворота f, а также считая, что
внешняя сила отсутствует, получим два уравнения - механическое и электрическое
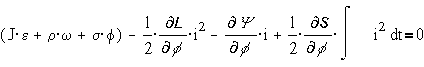
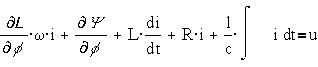
Из первого
(механического) уравнения получаем силы (в данном случае - моменты),
возникающие при электромеханическом преобразовании энергии :
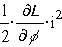 - сила (момент), вызванная
изменением индуктивности от изменения координаты (угла поворота) -
злектромагнитная сила,
- сила (момент), вызванная
изменением индуктивности от изменения координаты (угла поворота) -
злектромагнитная сила, 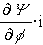 - сила (момент),
действующая на проводник (контур) с таком, помещенный в магнитный поток,-
магнитоэлектрический момент,
- сила (момент),
действующая на проводник (контур) с таком, помещенный в магнитный поток,-
магнитоэлектрический момент,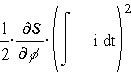 - сила (момент), вызванная
электрическим полем при механическом изменении емкости конденсатора .
- сила (момент), вызванная
электрическим полем при механическом изменении емкости конденсатора .
Реально в технике
применяются преобразователи, в которых действует только одна из перечисленных
сил - электромагнитные, магнитоэлектрические, электростатические.
Слагаемые второго,
электрического уравнения являются электрическими реакциями системы:
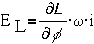 - противоЭДС, вызванная
изменением индуктивности при повороте контура с током (если индуктивность
изменяется, что происходит не всегда);
- противоЭДС, вызванная
изменением индуктивности при повороте контура с током (если индуктивность
изменяется, что происходит не всегда);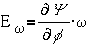 - ЭДС индукции, вызванная
вращением контура в магнитном поле;
- ЭДС индукции, вызванная
вращением контура в магнитном поле; 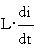 - ЭДС самоиндукции;
- ЭДС самоиндукции; 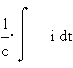 - напряжение конденсатора;
- напряжение конденсатора;
- R·i-
падение напряжения на сопротивлении.
Эквивалентная схема
электрической цепи такой системы имеет вид на  .
.
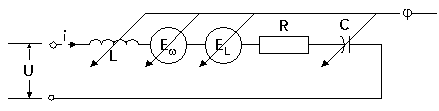
Рис. 1-1. Эквивалентная схема
гипотетической электромеханической системы
1.4. Электромагнитные,
электродинамические и электростатические преобразователи.
1.4.1. Электромагнитные
преобразователи.
В электромагнитном
преобразователе усилие создается за счет изменения магнитной энергии,
запасенной в катушке индуктивности L при перемещении сердечника.
Магнитная и энергия и энергия рассеяния имеют следующий вид:
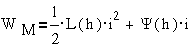 ,
, 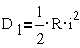
В этих системах 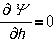 ,
поэтому дифференциальные уравнения имеют вид (при отсутствии внешней силы):
,
поэтому дифференциальные уравнения имеют вид (при отсутствии внешней силы):
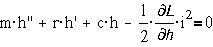 ;
;
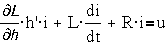
Типичным
преобразователем такого типа является электромагнитное реле, схема которого
приведена на  .
.
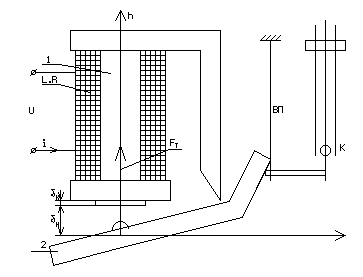
Рис. 1-2. Электромагнитное реле.
Реле представляет
собой электромагнит с контактами К. При подаче напряжения U на
обмотку электромагнита, имеющую индуктивность L и активное сопротивление R создается
электромагнитное тяговое усилие 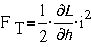 , которое притягивает якорь Р,
изменяя его положение относительно сердечника 1 (координату hот 0 до
d), при этом происходит переключение контактов
К.
, которое притягивает якорь Р,
изменяя его положение относительно сердечника 1 (координату hот 0 до
d), при этом происходит переключение контактов
К.
Из анализа
дифференциальных уравнений имеем:
- m·h``-
сила инерции,
- r·h`-
сила вязкого сопротивления, которой в реле можно пренебречь,
- c·h-
сила сопротивления возвратной пружины ВП, имеющей жесткость С,
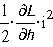 - тяговое усилие,
- тяговое усилие, 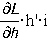 - ЭДС, вызванная
изменением индуктивности при перемещении якоря,
- ЭДС, вызванная
изменением индуктивности при перемещении якоря, 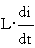 - ЭДС, вызванная
изменением тока,
- ЭДС, вызванная
изменением тока, - R·i-
падение напряжения на активном сопротивлении обмотки реле.
Итак, тяговое
усилие реле определяется изменением индуктивности L при перемещении якоря. При
показанной на  конструкции реле (клапанного типа) и малом перемещении
якоря можно считать, что
конструкции реле (клапанного типа) и малом перемещении
якоря можно считать, что
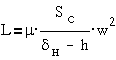 .
.
Тогда 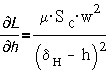 ,
откуда
,
откуда 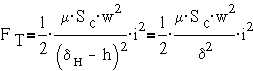 , где
, где 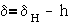 .
.
При включении репе
на постоянное напряжение, как эта обычно бывает, процесс описывается
нелинейными дифференциальными уравнениями:
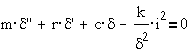
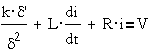 , где
, где 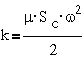
Тогда так
называемые тяговые характеристики реле имеют вид на  .
.
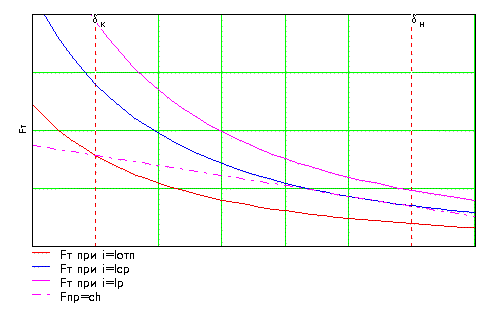
Рис. 1-3а. Механические
характеристики электромагнитного реле
Характеристики
вход-выход имеют скачкообразный характер ( ).
).
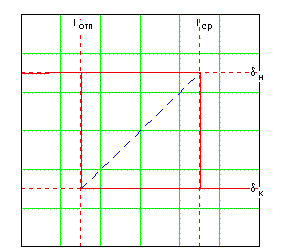
Рис. 1-3б. Характеристики
"вход-выход" электромагнитного реле.
Переходный процесс
при включении реле показан на  .
.
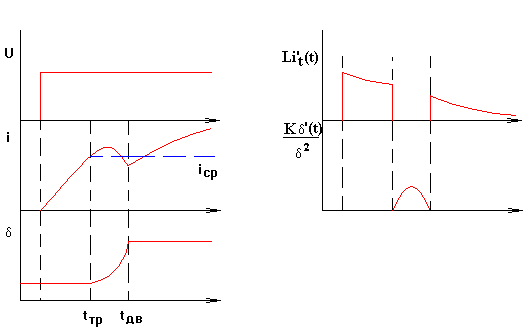
Рис. 1-4. Переходный процесс при
включении реле.
Модель
электромагнитного реле приведена в  .
.
1.4.2. Электродинамические
преобразователи.
В
магнитоэлектрической (электродинамической) системе усилие создается за счет
изменения второй составляющей магнитной энергии Y(h)×i. То есть уравнения имеют
следующий вид:
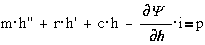 ;
;
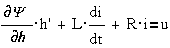
Электродинамический
принцип преобразования энергии используется в электроизмерительных приборах,
содержащих постоянный магнит, двигателях постоянного тока, тахогенераторах
постоянного тока. В этих устройствах обобщенной характеристикой является угол
поворота ротора f и уравнения имеют вид:
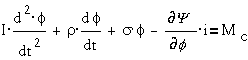 ;
;
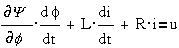
Обычно обозначают
угловую частоту вращения 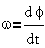 , тогда
, тогда
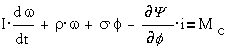 ;
;
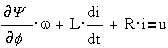
Здесь
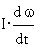 - момент сопротивления,
вызванный механической инерционностью системы (I - момент инерции
системы),
- момент сопротивления,
вызванный механической инерционностью системы (I - момент инерции
системы), - ρ·ω- момент вязкого
сопротивления,
- σ·f- момент упругого сопротивления,
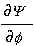 - вращающий момент,
- вращающий момент, - Mc- статический момент
сопротивления,
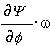 - ЭДС индукции (вращения),
- ЭДС индукции (вращения),
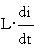 - ЭДС самоиндукции,
- ЭДС самоиндукции, - R·i- падение
напряжения на активном сопротивлении.
При применении
преобразователя как исполнительного устройства (измерительного прибора)
используется факт возникновения магнитоэлектрического вращающего момента,
пропорционального току в цепи ротора. При применении его как датчика скорости
используется возникновение в цепи ЭДС индукции, пропорциональной частоте
вращения ротора. В этом случае электрическое уравнение преобразователя имеет
вид :
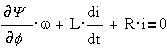
И в установившемся
режиме, когда 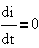 , имеем
, имеем 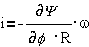 .
.
В частности, при
повороте в магнитном поле с индукцией B рамки длиной 1 и радиусом r имеем dΨ=r·ω·B·1·r·df, откуда 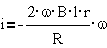 .
.
Основным
достоинством электродинамических систем является линейность их характеристик.
1.4.3. Электростатические преобразователи.
В
электростатических системах используется энергия электрического поля,
запасенная в конденсаторе
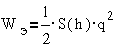 ;
;
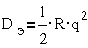
В этом случае
дифференциальные уравнения таковы:
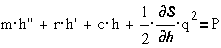 ;
;
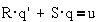
Здесь 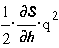 -
тяговое усилие, S×q- напряжение на конденсаторе
-
тяговое усилие, S×q- напряжение на конденсаторе
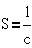 .
.
Эти уравнения имеют
меньше слагаемых, чем уравнения индукционных систем, поэтому электростатические
преобразователи обладают меньшими возможностями и получили меньшее
распространение.
Исполнительные
устройства электростатического типа очень маломощны, так как электрическое поле
в единице объема может сконцентрировать гораздо меньше энергии, чем магнитное.
Поэтому тяговое усилие 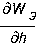 сравнительно небольшое. Исполнительные устройства
такого типа применяются в основном как измерительные и индикаторные.
сравнительно небольшое. Исполнительные устройства
такого типа применяются в основном как измерительные и индикаторные.
Возможности
электростатического преобразователя как датчика, как видно из электрического
уравнения, также ограничены, так как он не может индуцировать ЭДС и является,
по существу, пассивным емкостным датчиком с уравнением вида:
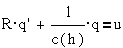
Обозначив Uc- напряжение на конденсаторе, получим :
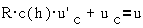
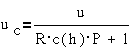
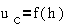
Пассивный емкостной
преобразователь переменного тока.
1.5. Классификация
электромеханических преобразователей
Электромеханические
преобразователи, применяемые в системах автоматики и вычислительной технике,
можно классифицировать по назначению, конструктивному исполнению и принципу
действия (см.  ).
).
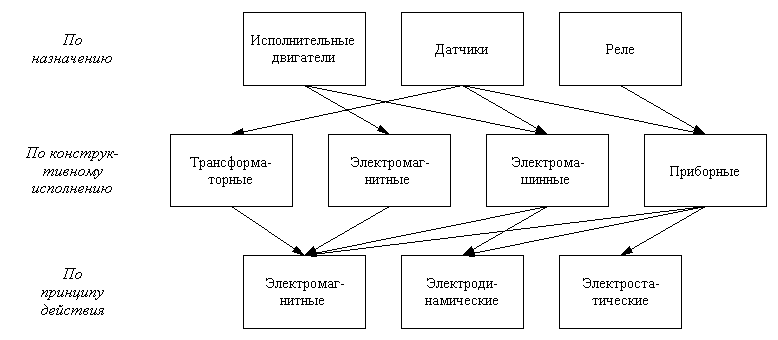 Рис.
1-5. Классификация электромеханических преобразователей.
Рис.
1-5. Классификация электромеханических преобразователей.
1.6. Представление
электромеханических преобразователей как преобразователей сигналов (информации)
При применении
электромеханических преобразователей в системах автоматического управления они
рассматриваются не как энергетические устройства, а как информационные
преобразователи сигналов при их прохождении от входов к выходам (см.  ).
).
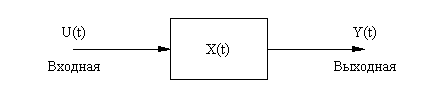
Рис. 1-6а. Функциональная схема
динамической системы.
Если
электромеханический преобразователь описывается исходными линейными или
линеаризованными дифференциальными уравнениями, то от них можно перейти к
дифференциальным уравнениям "вход-выход" вида
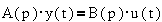
где y(t) и u(t) -
векторы выходных и входных координат
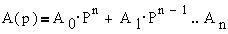 ;
; 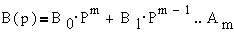 -
полиномиальные матрицы,
-
полиномиальные матрицы,
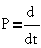 - оператор
дифференцирования по времени.
- оператор
дифференцирования по времени.
Перейти от исходных
энергетических уравнений к уравнениям "вход-выход" удобно, используя
структурные схемы и передаточные функции. Типичная структурная схема имеет вид,
представленный на  ,
где W(p) - передаточные функции, а u(p), y(p), i(p) - изображения входных,
выходных и внутренних переменных (p=c+j·ω).
,
где W(p) - передаточные функции, а u(p), y(p), i(p) - изображения входных,
выходных и внутренних переменных (p=c+j·ω).
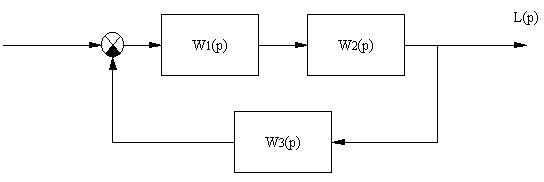
Рис. 1-6б. Структурная схема
динамической системы.
Уравнение
"вход-выход" получим в виде:
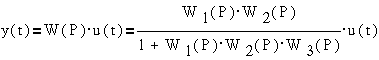 ,
,
где 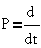
Структурная схема
тесно связана с физикой работы преобразователя и поэтому легко может быть
составлена по исходным энергетическим уравнениям, а уравнения "вход-выход"
представляют более абстрактную модель системы.
Можно перейти к еще
более абстрактной модели - уравнениям состояния, когда система представляется
стандартной структурой в виде автомата с памятью ( ).
).
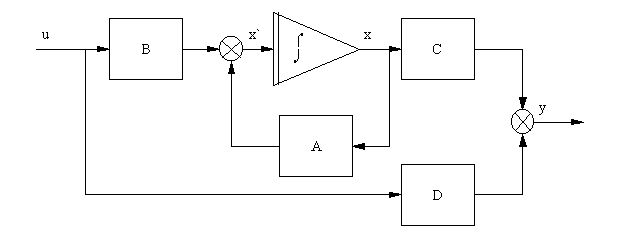
Рис. 1-7а. Структурная схема
динамической системы в виде непрерывного автомата.
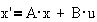 ;
;
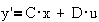 ,
,
где x-
вектор состояния, A- матрица коэффициентов, B- матрица управления, C-
матрица выхода, D - матрица обхода.
В этой структуре
переменные состояния часто не являются физическими величинами, которые могут
быть измерены в реальной системе.
Для моделирования
электромеханической системы на ЭВМ или при управлении ею от ЭВМ удобно эту
систему представить как дискретную по времени (импульсную), в которой ее
переменные наблюдаются (вычисляются) через дискретные промежутки времени Т. При
выборе Т достаточно малом по сравнению с инерционностью системы, дискретная
модель достаточно точно описывает непрерывную систему.
Для анализа
дискретной модели вводится аппарат дискретного преобразования Лапласа и
дискретные передаточные функции D(Z), где Z-
оператор запаздывания на интервал Т .
При достаточно
малом Т можно принять 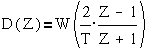 .
.
Имея передаточную
функцию системы W(P), заменой 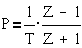 получим D(Z) в
виде
получим D(Z) в
виде
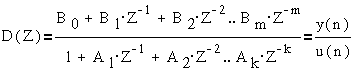 ,
,
где Z-1- запаздывание на один такт
(время Т). Этой функции соответствует разностное уравнение
"вход-выход"
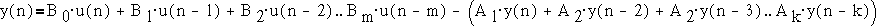
Этой модели
соответствует дискретный рекурсивный фильтр вида 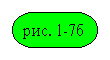 , где А и В
-полиномиальные матрицы, а Т - матрица задержек тактов.
, где А и В
-полиномиальные матрицы, а Т - матрица задержек тактов.
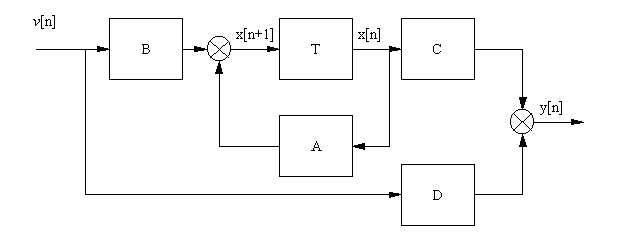
Рис. 1-7б. Структурная схема
динамической системы в виде дискретного автомата.
По схеме
рекурсивного фильтра может быть восстановлен алгоритм вычисления выходной
величины y(n) в данном такте, зная y(n-i) в
предыдущие такты, и значения входного воздействия u(n) в данный такт и u(n-i) в
предыдущие такты - прямое программирование. Применяются также последовательное
и параллельное программирование, когда D(Z) представляется в виде
произведения или суммы более простых функций.
От разностных
уравнений "вход-выход" можно перейти к уравнениям пространства
состояний и представить систему в виде дискретного автомата с памятью в виде  .
.
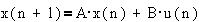 ;
; 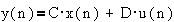
где x[n] -
состояние в данный такт, x[n+1] - состояние в следующий такт.
Удобной моделью для
анализа динамической системы является частотная характеристика
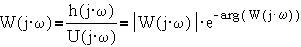
которая обычно
представляется в виде двух характеристик, амплитудной A(ω) и фазовой f(ω).
1.7. Анализ простейшего
электромеханического преобразователя.
Рассмотрим
простейший магнитоэлектрический преобразователь, имеющий одну степень
механической н электрической свободы, в качестве которого может быть приведен
линейный исполнительный двигатель, применяемый в системе позиционирования в
накопителях на жестких дисках СМ-ЭВМ.
Его динамика
описывается двумя уравнениями:
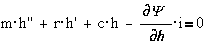
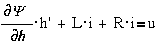
Модель такого
преобразователя приведена на  и
и  .
.
Обозначив 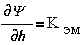 и
и 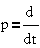 ,
получим эти уравнения в операторной форме:
,
получим эти уравнения в операторной форме:
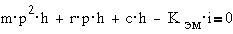
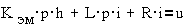
Перейдя к
изображениям, получим следующие уравнения:
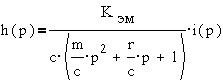
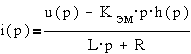
По этим уравнениям
можно получить структурную схему согласно  , по которой можно получить передаточную функцию
, по которой можно получить передаточную функцию
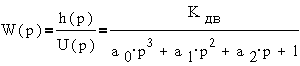
где 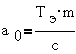 ;
; 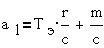 ;
; 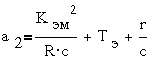
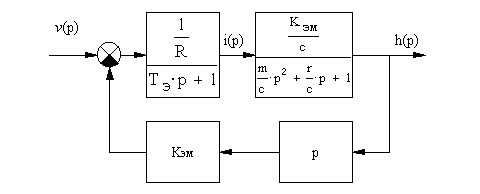
Рис. 1-8. Структурная схема
электромеханического преобразователя.
Перейдя обратно во
временную область, можно получить уравнение "вход-выход"
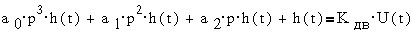 , где
, где 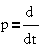
Для перехода к
уравнениям состояния представим уравнение вход-выход в скобочной форме
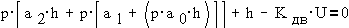
Введем новые
координаты, соответствующие перемещенным в квадратных скобках и получим
дифференциально-алгебраическую систему (слева) и ее преобразованную форму
(справа)
Этим уравнениям
соответствует структура, показанная на  .
.
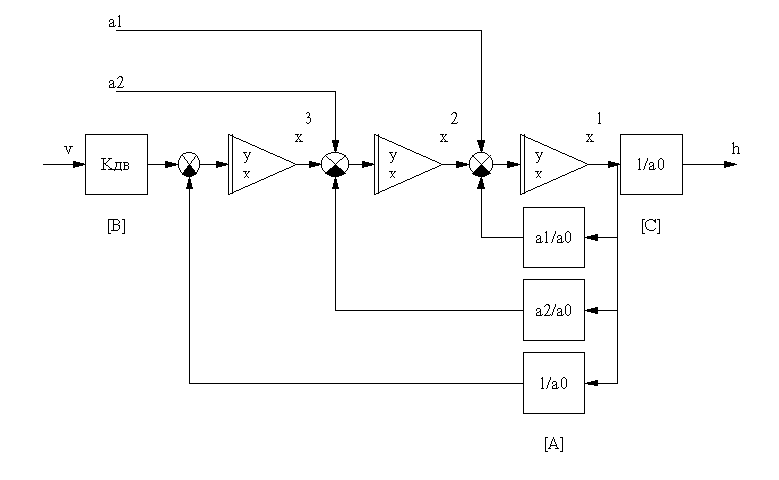 Рис.
1-9. Структурная схема преобразователя в пространстве состояния.
Рис.
1-9. Структурная схема преобразователя в пространстве состояния.
При переходе к
уравнениям состояния получим x`=A·x+B·u; h=C·x+D·u,
где u=U; 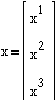 ;
; 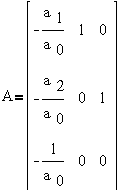 ;
;
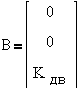 ;
; 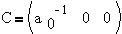 ; D=0.
; D=0.
При достаточно
малом периоде квантования Т по сравнению с инерционностью системы ее можно
представить как дискретную (по времени) с дискретной передаточной функцией
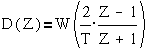
Произведя
необходимые преобразования, получим
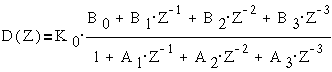
где 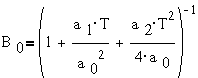 ;
; 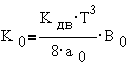 ;
B1=B2=3·B0; B3=B0.
;
B1=B2=3·B0; B3=B0.
Обозначим h`=h·K0-1.Тогда из выражения 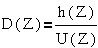 получим
разностное уравнение "вход-выход":
получим
разностное уравнение "вход-выход":
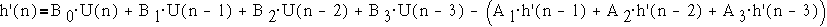
Этому уравнению соответствует
структура рекурсивного фильтра, представленная на  .
.
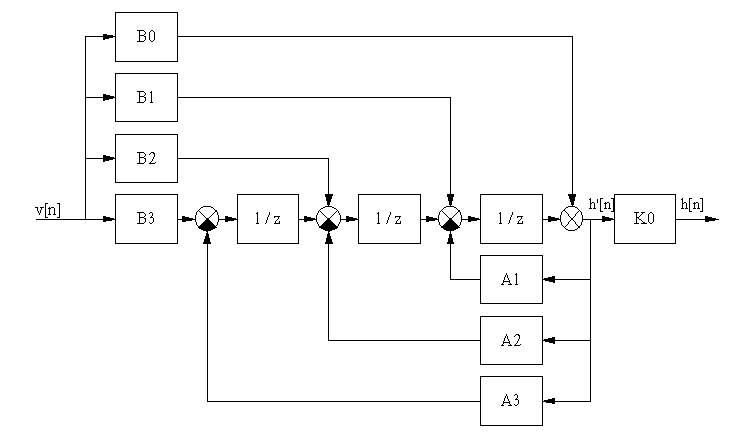
Рис. 1-10а. Структурная схема
преобразователя в виде рекурсивного фильтра.
Используя,
например, прямое программирование, можно моделировать систему на ЭВМ, вычисляя
значения выходной величины h(n) по шагам. Скажем,
переходную функцию при ступенчатом воздействии
U(n)=U при n>0 (см. 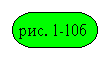 )
)
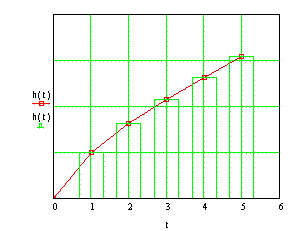
Рис. 1-10б. Выход преобразователя при
ступенчатом воздействии.
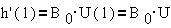
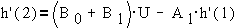
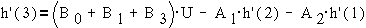
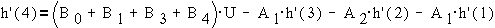
и.т.д.
От разностного
уравнения вход-выход можно перейти к уравнениям состояния и представить систему
в виде дискретного автомата с памятью
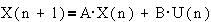 ;
; 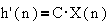
- X(n)
- вектор состояния автомата в данный дискретный момент времени,
- X(n+1)
- вектор состояния в следующий наблюдаемый момент через промежуток времени
Т,
- B- матрица входного
преобразования,
- A- матрица, реализующая
функцию переходов,
- C- матрица, соответствующая
функции выходов.
Частотная
характеристика системы
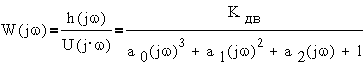
В этом случае, если
характеристическое уравнение имеет вещественные отрицательные корни, получим
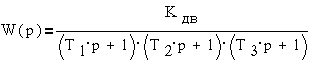
где T1·T2·T3=a0; T1·T2+T1·T3+T2·T3=a1; T1+T2+T3=a2, а корни α1=-T1-1; α2=-T2-1; α3=-T3-1.
Тогда амплитудная
частотная характеристика будет (см. )
)
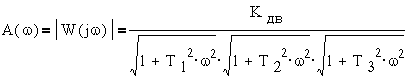
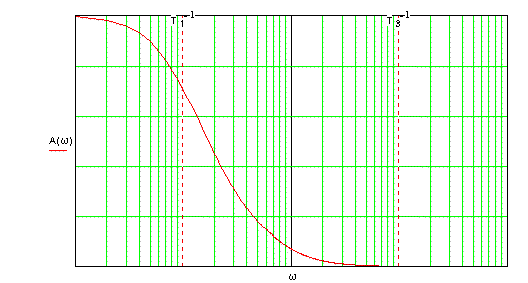
Рис. 1-11. Частотная характеристика
электромеханического преобразователя.
1.8. Упражнения и контрольные вопросы к главе 1.
- Перечислите основные механические аналогии, дополнив колонки 1 и 2 таблицы 1-1 размерностями представленных в них физических величин.
- Выведите уравнения динамики простейших механической и электромеханической систем из уравнений Лагранжа-Максвелла. Нарисуйте схемы, соответствующие этим уравнениям.
- Перечислите основные типы электромеханических преобразователей и приведите примеры этих преобразователей.
- Выведите передаточную функцию и нарисуйте структурную схему линейного двигателя без пружины и без трения.
- По полученной в п.4 передаточной функции выведите выражение для частотной характеристики двигателя и постройте ее, задавшись численными значениями параметров двигателя (например, Тэ=10 мс, m=50 г, Кэм=0,05 Вс).
|

 .
.  Рис.
1-9. Структурная схема преобразователя в пространстве состояния.
Рис.
1-9. Структурная схема преобразователя в пространстве состояния.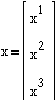
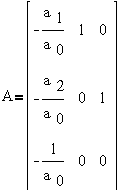
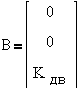
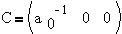
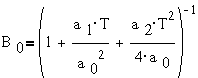
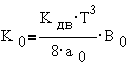
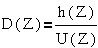
 .
.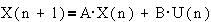
 )
) 


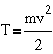 для
поступательного движения и
для
поступательного движения и 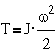 для вращательного
движения;
для вращательного
движения; 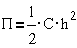 , где
, где 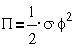 , где
, где 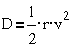 или
или
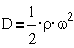 в зависимости от формы движения.
в зависимости от формы движения. 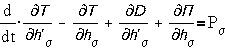 ,
, 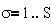 .
. 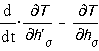 - Даламберовы силы
инерции,
- Даламберовы силы
инерции, 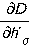 -силы трения,
-силы трения, 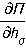 - силы упругого
противодействия,
- силы упругого
противодействия, 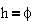 ;
; 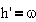 ;
; 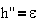
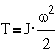 ;
; 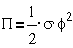 ;
; 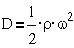 ;
; 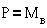
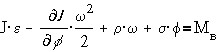 .
. 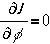 и
уравнение принимает вид:
и
уравнение принимает вид: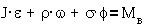 .
. 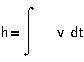
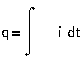
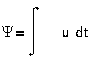
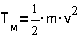
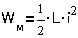
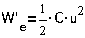
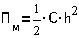
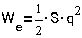
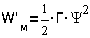
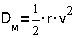
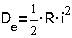
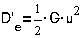
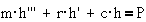
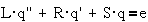
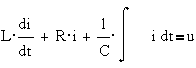
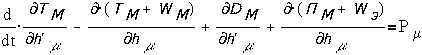 ,
, 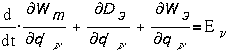
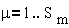
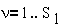
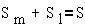
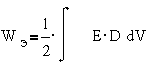 ,
,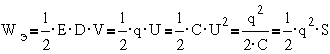
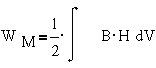
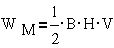
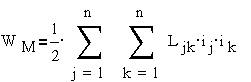 ,
,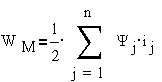 , где
, где 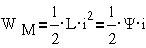
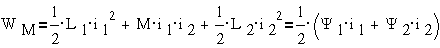 ;
; 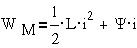 ,
,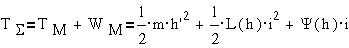 ;
; 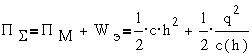 ;
; 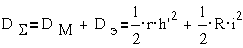
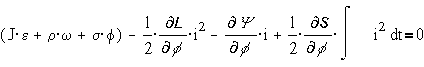
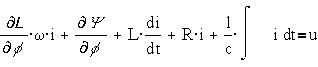
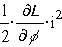 - сила (момент), вызванная
изменением индуктивности от изменения координаты (угла поворота) -
злектромагнитная сила,
- сила (момент), вызванная
изменением индуктивности от изменения координаты (угла поворота) -
злектромагнитная сила, 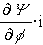 - сила (момент),
действующая на проводник (контур) с таком, помещенный в магнитный поток,-
магнитоэлектрический момент,
- сила (момент),
действующая на проводник (контур) с таком, помещенный в магнитный поток,-
магнитоэлектрический момент,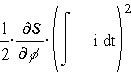 - сила (момент), вызванная
электрическим полем при механическом изменении емкости конденсатора .
- сила (момент), вызванная
электрическим полем при механическом изменении емкости конденсатора .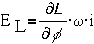 - противоЭДС, вызванная
изменением индуктивности при повороте контура с током (если индуктивность
изменяется, что происходит не всегда);
- противоЭДС, вызванная
изменением индуктивности при повороте контура с током (если индуктивность
изменяется, что происходит не всегда);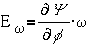 - ЭДС индукции, вызванная
вращением контура в магнитном поле;
- ЭДС индукции, вызванная
вращением контура в магнитном поле; 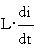 - ЭДС самоиндукции;
- ЭДС самоиндукции; 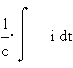 - напряжение конденсатора;
- напряжение конденсатора;


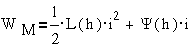 ,
, 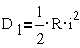
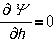 ,
поэтому дифференциальные уравнения имеют вид (при отсутствии внешней силы):
,
поэтому дифференциальные уравнения имеют вид (при отсутствии внешней силы): 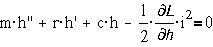 ;
; 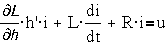


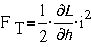 , которое притягивает якорь Р,
изменяя его положение относительно сердечника 1 (координату
, которое притягивает якорь Р,
изменяя его положение относительно сердечника 1 (координату 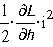 - тяговое усилие,
- тяговое усилие, 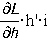 - ЭДС, вызванная
изменением индуктивности при перемещении якоря,
- ЭДС, вызванная
изменением индуктивности при перемещении якоря, 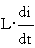 - ЭДС, вызванная
изменением тока,
- ЭДС, вызванная
изменением тока, 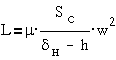 .
.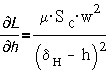 ,
откуда
,
откуда 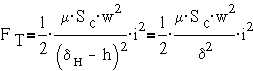 , где
, где 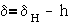 .
.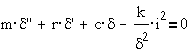
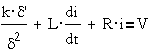 , где
, где 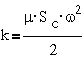





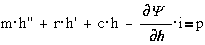 ;
; 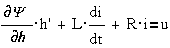
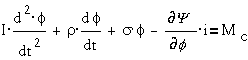 ;
;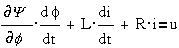
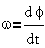 , тогда
, тогда 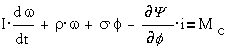 ;
; 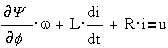
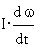 - момент сопротивления,
вызванный механической инерционностью системы (
- момент сопротивления,
вызванный механической инерционностью системы (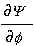 - вращающий момент,
- вращающий момент, 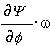 - ЭДС индукции (вращения),
- ЭДС индукции (вращения),
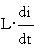 - ЭДС самоиндукции,
- ЭДС самоиндукции, 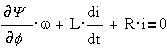
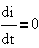 , имеем
, имеем 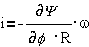 .
.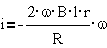 .
. 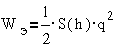 ;
; 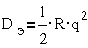
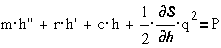 ;
; 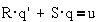
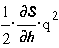 -
тяговое усилие,
-
тяговое усилие, 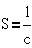 .
.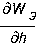 сравнительно небольшое. Исполнительные устройства
такого типа применяются в основном как измерительные и индикаторные.
сравнительно небольшое. Исполнительные устройства
такого типа применяются в основном как измерительные и индикаторные. 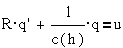
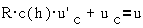
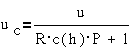
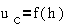

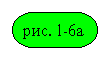
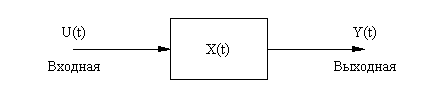
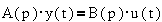
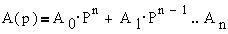 ;
; 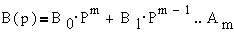 -
полиномиальные матрицы,
-
полиномиальные матрицы, 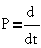 - оператор
дифференцирования по времени.
- оператор
дифференцирования по времени. 

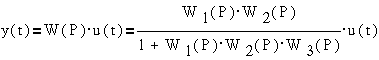 ,
,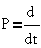

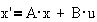 ;
; 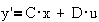 ,
,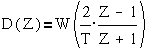 .
.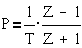 получим
получим 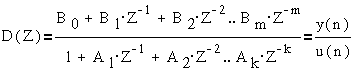 ,
,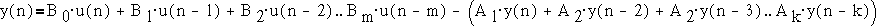

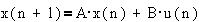 ;
; 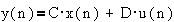
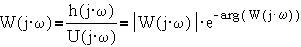
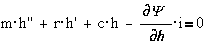
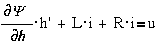


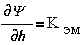 и
и 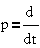 ,
получим эти уравнения в операторной форме:
,
получим эти уравнения в операторной форме: 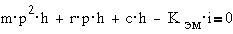
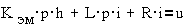
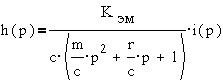
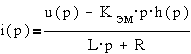

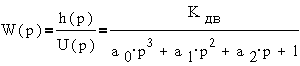
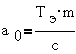 ;
; 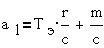 ;
; 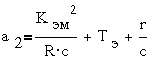

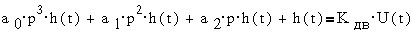 , где
, где